个人中心
gpt4 book ai didi

使用C语言详解霍夫曼树数据结构

转载 作者：qq735679552 更新时间：2022-09-27 22:32:09 27 4
gpt4 key购买 nike

CFSDN坚持开源创造价值，我们致力于搭建一个资源共享平台，让每一个IT人在这里找到属于你的精彩世界.

这篇CFSDN的博客文章使用C语言详解霍夫曼树数据结构由作者收集整理，如果你对这篇文章有兴趣，记得点赞哟.

1、基本概念 。

a、路径和路径长度 。

若在一棵树中存在着一个结点序列 k1，k2，……，kj， 使得 ki是ki+1 的双亲（1<=i<j），则称此结点序列是从 k1 到 kj 的路径.

从 k1 到 kj 所经过的分支数称为这两点之间的路径长度，它等于路径上的结点数减1. 。

b、结点的权和带权路径长度 。

在许多应用中，常常将树中的结点赋予一个有着某种意义的实数，我们称此实数为该结点的权，(如下面一个树中的蓝色数字表示结点的权) 。

结点的带权路径长度规定为从树根结点到该结点之间的路径长度与该结点上权的乘积.

c、树的带权路径长度 。

树的带权路径长度定义为树中所有叶子结点的带权路径长度之和，公式为:

使用C语言详解霍夫曼树数据结构

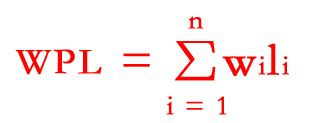
 其中，n表示叶子结点的数目，wi 和 li 分别表示叶子结点 ki 的权值和树根结点到 ki 之间的路径长度.

如下图中树的带权路径长度 WPL = 9 x 2 + 12 x 2 + 15 x 2 + 6 x 3 + 3 x 4 + 5 x 4  =  122 。

  。

d、哈夫曼树 。

哈夫曼树又称最优二叉树。它是 n 个带权叶子结点构成的所有二叉树中，带权路径长度 WPL 最小的二叉树.

如下图为一哈夫曼树示意图.

使用C语言详解霍夫曼树数据结构

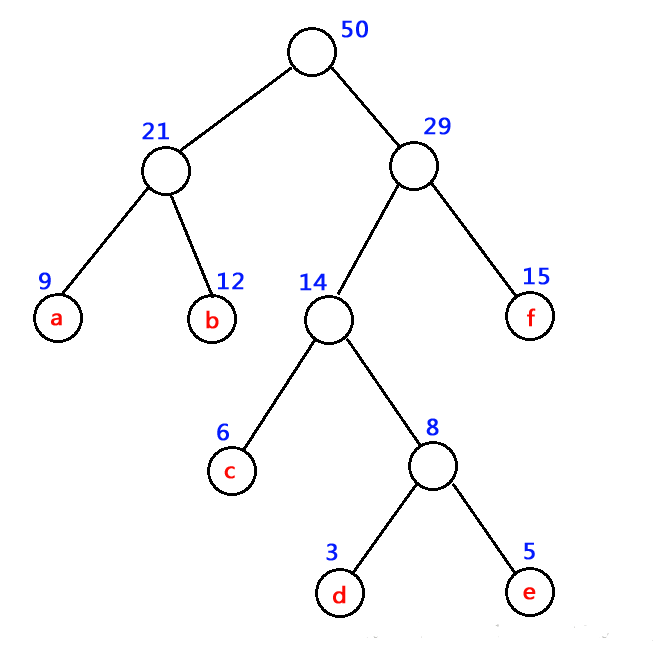
2、构造哈夫曼树 。

假设有n个权值，则构造出的哈夫曼树有n个叶子结点。 n个权值分别设为 w1、w2、…、wn，则哈夫曼树的构造规则为:

(1) 将w1、w2、…，wn看成是有n 棵树的森林(每棵树仅有一个结点)； 。

(2) 在森林中选出两个根结点的权值最小的树合并，作为一棵新树的左、右子树，且新树的根结点权值为其左、右子树根结点权值之和； 。

(3)从森林中删除选取的两棵树，并将新树加入森林； 。

(4)重复(2)、(3)步，直到森林中只剩一棵树为止，该树即为所求得的哈夫曼树.

 如：对 下图中的六个带权叶子结点来构造一棵哈夫曼树，步骤如下:

使用C语言详解霍夫曼树数据结构

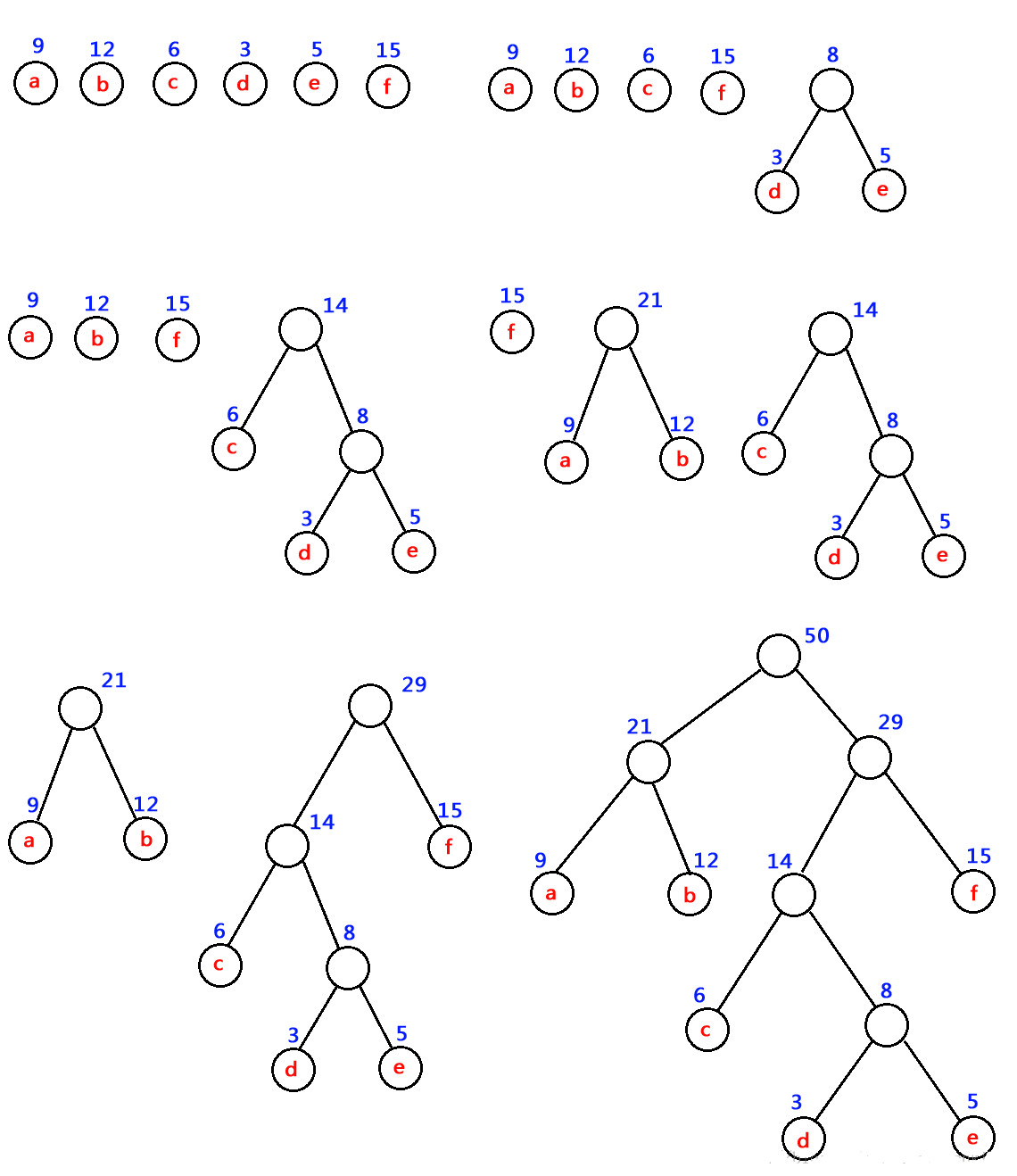
  注意：为了使得到的哈夫曼树的结构尽量唯一，通常规定生成的哈夫曼树中每个结点的左子树根结点的权小于等于右子树根结点的权.

具体算法如下:

    。

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
//2、根据数组 a 中 n 个权值建立一棵哈夫曼树，返回树根指针
  struct BTreeNode* CreateHuffman(ElemType a[], int n)
  {
    int i, j;
    struct BTreeNode **b, *q;
    b = malloc (n* sizeof ( struct BTreeNode));
    for (i = 0; i < n; i++) //初始化b指针数组，使每个指针元素指向a数组中对应的元素结点
    {
      b[i] = malloc ( sizeof ( struct BTreeNode));
      b[i]->data = a[i];
      b[i]->left = b[i]->right = NULL;
    }
    for (i = 1; i < n; i++) //进行 n-1 次循环建立哈夫曼树
    {
      //k1表示森林中具有最小权值的树根结点的下标，k2为次最小的下标
      int k1 = -1, k2;
      for (j = 0; j < n; j++) //让k1初始指向森林中第一棵树，k2指向第二棵
      {
        if (b[j] != NULL && k1 == -1)
        {
          k1 = j;
          continue ;
        }
        if (b[j] != NULL)
        {
          k2 = j;
          break ;
        }
      }
      for (j = k2; j < n; j++) //从当前森林中求出最小权值树和次最小
      {
        if (b[j] != NULL)
        {
          if (b[j]->data < b[k1]->data)
          {
            k2 = k1;
            k1 = j;
          }
          else if (b[j]->data < b[k2]->data)
            k2 = j;
        }
      }
      //由最小权值树和次最小权值树建立一棵新树，q指向树根结点
      q = malloc ( sizeof ( struct BTreeNode));
      q->data = b[k1]->data + b[k2]->data;
      q->left = b[k1];
      q->right = b[k2];
  
      b[k1] = q; //将指向新树的指针赋给b指针数组中k1位置
      b[k2] = NULL; //k2位置为空
    }
    free (b); //删除动态建立的数组b
    return q; //返回整个哈夫曼树的树根指针
  }

3、哈夫曼编码 。

在电报通信中，电文是以二进制的0、1序列传送的，每个字符对应一个二进制编码，为了缩短电文的总长度，采用不等长编码方式，构造哈夫曼树， 。

将每个字符的出现频率作为字符结点的权值赋予叶子结点，每个分支结点的左右分支分别用0和1编码，从树根结点到每个叶子结点的路径上 。

所经分支的0、1编码序列等于该叶子结点的二进制编码。如上文所示的哈夫曼编码如下:

使用C语言详解霍夫曼树数据结构

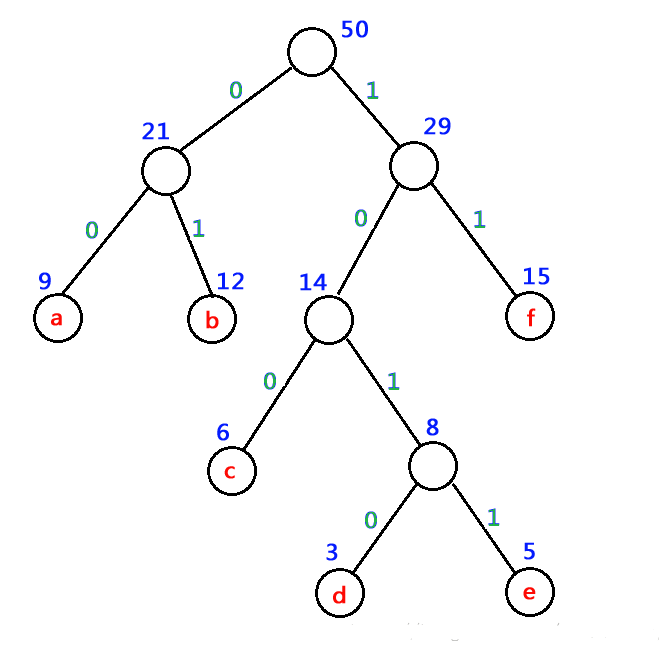
 a 的编码为：00 。

b 的编码为：01 。

c 的编码为：100 。

d 的编码为：1010 。

e 的编码为：1011 。

f 的编码为：11 。

4、哈夫曼树的操作运算 。

以上文的哈夫曼树作为具体实例，用详细的程序展示哈夫曼树的操作运算 。

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
#include<stdio.h>
#include<stdlib.h>
typedef int ElemType;
struct BTreeNode
{
  ElemType data;
  struct BTreeNode* left;
  struct BTreeNode* right;
};
 
//1、输出二叉树，可在前序遍历的基础上修改。采用广义表格式，元素类型为int
void PrintBTree_int( struct BTreeNode* BT)
{
  if (BT != NULL)
  {
   printf ( "%d" , BT->data); //输出根结点的值
   if (BT->left != NULL || BT->right != NULL)
   {
    printf ( "(" );
    PrintBTree_int(BT->left); //输出左子树
    if (BT->right != NULL)
     printf ( "," );
    PrintBTree_int(BT->right); //输出右子树
    printf ( ")" );
   }
  }
}
 
//2、根据数组 a 中 n 个权值建立一棵哈夫曼树，返回树根指针
struct BTreeNode* CreateHuffman(ElemType a[], int n)
{
  int i, j;
  struct BTreeNode **b, *q;
  b = malloc (n* sizeof ( struct BTreeNode));
  for (i = 0; i < n; i++) //初始化b指针数组，使每个指针元素指向a数组中对应的元素结点
  {
   b[i] = malloc ( sizeof ( struct BTreeNode));
   b[i]->data = a[i];
   b[i]->left = b[i]->right = NULL;
  }
  for (i = 1; i < n; i++) //进行 n-1 次循环建立哈夫曼树
  {
   //k1表示森林中具有最小权值的树根结点的下标，k2为次最小的下标
   int k1 = -1, k2;
   for (j = 0; j < n; j++) //让k1初始指向森林中第一棵树，k2指向第二棵
   {
    if (b[j] != NULL && k1 == -1)
    {
     k1 = j;
     continue ;
    }
    if (b[j] != NULL)
    {
     k2 = j;
     break ;
    }
   }
   for (j = k2; j < n; j++) //从当前森林中求出最小权值树和次最小
   {
    if (b[j] != NULL)
    {
     if (b[j]->data < b[k1]->data)
     {
      k2 = k1;
      k1 = j;
     }
     else if (b[j]->data < b[k2]->data)
      k2 = j;
    }
   }
   //由最小权值树和次最小权值树建立一棵新树，q指向树根结点
   q = malloc ( sizeof ( struct BTreeNode));
   q->data = b[k1]->data + b[k2]->data;
   q->left = b[k1];
   q->right = b[k2];
 
   b[k1] = q; //将指向新树的指针赋给b指针数组中k1位置
   b[k2] = NULL; //k2位置为空
  }
  free (b); //删除动态建立的数组b
  return q; //返回整个哈夫曼树的树根指针
}
 
//3、求哈夫曼树的带权路径长度
ElemType WeightPathLength( struct BTreeNode* FBT, int len) //len初始为0
{
  if (FBT == NULL) //空树返回0
   return 0;
  else
  {
   if (FBT->left == NULL && FBT->right == NULL) //访问到叶子结点
    return FBT->data * len;
   else //访问到非叶子结点，进行递归调用，返回左右子树的带权路径长度之和，len递增
    return WeightPathLength(FBT->left,len+1)+WeightPathLength(FBT->right,len+1);
  }
}
 
//4、哈夫曼编码（可以根据哈夫曼树带权路径长度的算法基础上进行修改）
void HuffManCoding( struct BTreeNode* FBT, int len) //len初始值为0
{
  static int a[10]; //定义静态数组a，保存每个叶子的编码，数组长度至少是树深度减一
  if (FBT != NULL) //访问到叶子结点时输出其保存在数组a中的0和1序列编码
  {
   if (FBT->left == NULL && FBT->right == NULL)
   {
    int i;
    printf ( "结点权值为%d的编码：" , FBT->data);
    for (i = 0; i < len; i++)
     printf ( "%d" , a[i]);
    printf ( "\n" );
   }
   else //访问到非叶子结点时分别向左右子树递归调用，并把分支上的0、1编码保存到数组a
   { //的对应元素中，向下深入一层时len值增1
    a[len] = 0;
    HuffManCoding(FBT->left, len + 1);
    a[len] = 1;
    HuffManCoding(FBT->right, len + 1);
   }
  }
}
 
//主函数
void main()
{
  int n, i;
  ElemType* a;
  struct BTreeNode* fbt;
  printf ( "从键盘输入待构造的哈夫曼树中带权叶子结点数n：" );
  while (1)
  {
   scanf ( "%d" , &n);
   if (n > 1)
    break ;
   else
    printf ( "重输n值：" );
  }
  a = malloc (n* sizeof (ElemType));
  printf ( "从键盘输入%d个整数作为权值：" , n);
  for (i = 0; i < n; i++)
   scanf ( " %d" , &a[i]);
  fbt = CreateHuffman(a, n);
  printf ( "广义表形式的哈夫曼树：" );
  PrintBTree_int(fbt);
  printf ( "\n" );
  printf ( "哈夫曼树的带权路径长度：" );
  printf ( "%d\n" , WeightPathLength(fbt, 0));
  printf ( "树中每个叶子结点的哈夫曼编码：\n" );
  HuffManCoding(fbt, 0);
}

运行结果:

使用C语言详解霍夫曼树数据结构

  。

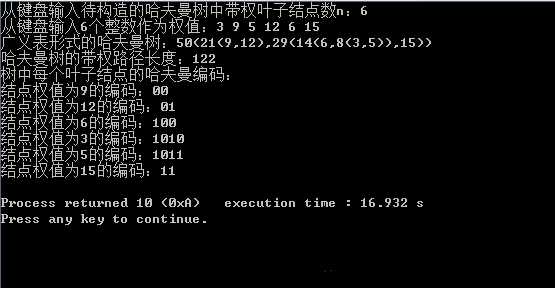
下面来看一道ACM题目 。

    题目描述：      哈夫曼树，第一行输入一个数n，表示叶结点的个数。需要用这些叶结点生成哈夫曼树，根据哈夫曼树的概念，这些结点有权值，即weight，题目需要输出所有结点的值与权值的乘积之和。      输入：      输入有多组数据。      每组第一行输入一个数n，接着输入n个叶节点（叶节点权值不超过100，2<=n<=1000）。      输出：      输出权值。      样例输入：      5        1 2 2 5 9      样例输出：      37  。

ac代码 。

链表构建哈夫曼树（插入排序） 。

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
#include <stdio.h>
#include <stdlib.h>
#define max 1001
 
struct htree
{
  int weight;
  struct htree *lchild;
  struct htree *rchild;
  struct htree *next;
};
 
void addNode( struct htree *, struct htree *);
struct htree* createHfmtree( int *, int );
int getWpl( struct htree *, int );
 
int main()
{
  int w[max];
  int i, n, wpl;
  struct htree *ht;
 
  while ( scanf ( "%d" , &n) != EOF)
  {
   for (i = 0; i < n; i ++)
   {
    scanf ( "%d" , &w[i]);
   }
   
   ht = createHfmtree(w, n);
   wpl = getWpl(ht, 0);
   printf ( "%d\n" , wpl);
  }
  return 0;
}
 
struct htree* createHfmtree( int *w, int n)
{
  int i;
  struct htree *head, *pl, *pr, *proot;
  head = ( struct htree *) malloc ( sizeof ( struct htree));
  head->next = NULL;
 
  for (i = 0; i < n; i ++)
  {
   struct htree *pnode = malloc ( sizeof ( struct htree));
   pnode->weight = *(w + i);
   pnode->lchild = pnode->rchild = pnode->next = NULL;
   addNode(head, pnode);
  }
 
  while (head->next)
  {
   if (head->next->next == NULL)
    break ;
   pl = head->next;
   pr = pl->next;
   head->next = pr->next;
   proot = ( struct htree *) malloc ( sizeof ( struct htree));
   proot->weight = pl->weight + pr->weight;
   proot->lchild = pl;
   proot->rchild = pr;
   addNode(head, proot);
  }
  return head->next;
}
 
void addNode( struct htree *head, struct htree *pnode)
{
  struct htree *t = head;
 
  while (t->next && t->next->weight < pnode->weight)
   t = t->next;
  pnode->next = t->next;
  t->next = pnode;
}
 
int getWpl( struct htree *ht, int level)
{
  if (ht == NULL)
   return 0;
  if (!ht->lchild && !ht->rchild)
  {
   return ht->weight * level;
  }
 
  return getWpl(ht->lchild, level + 1) + getWpl(ht->rchild, level + 1);
}

最后此篇关于使用C语言详解霍夫曼树数据结构的文章就讲到这里了,如果你想了解更多关于使用C语言详解霍夫曼树数据结构的内容请搜索CFSDN的文章或继续浏览相关文章，希望大家以后支持我的博客！ 。

27 4 0
文章推荐： 安装SqlServer2005时版本变更检查 (警告)
文章推荐： Win2008中安装的MSSQL2005后无法访问的解决方法
文章推荐： 如何在SQL Server 2005数据库中导入SQL Server 2008的数据
文章推荐： python3调用R的示例代码
qq735679552
个人简介

我是一名优秀的程序员,十分优秀！

滴滴打车优惠券免费领取
滴滴打车优惠券
Copyright 2021 - 2024 cfsdn All Rights Reserved 蜀ICP备2022000587号
广告合作:1813099741@qq.com 6ren.com