PyTorch: Softmax多分类实战操作-6ren

PyTorch: Softmax多分类实战操作

转载作者：qq735679552 更新时间：2022-09-29 22:32:09

CFSDN坚持开源创造价值，我们致力于搭建一个资源共享平台，让每一个IT人在这里找到属于你的精彩世界.

这篇CFSDN的博客文章PyTorch: Softmax多分类实战操作由作者收集整理，如果你对这篇文章有兴趣，记得点赞哟.

多分类一种比较常用的做法是在最后一层加softmax归一化，值最大的维度所对应的位置则作为该样本对应的类。本文采用PyTorch框架，选用经典图像数据集mnist学习一波多分类.

MNIST数据集。

MNIST 数据集(手写数字数据集)来自美国国家标准与技术研究所, National Institute of Standards and Technology (NIST). 训练集 (training set) 由来自 250 个不同人手写的数字构成, 其中 50% 是高中学生, 50% 来自人口普查局 (the Census Bureau) 的工作人员. 测试集(test set) 也是同样比例的手写数字数据。MNIST数据集下载地址:http://yann.lecun.com/exdb/mnist/。手写数字的MNIST数据库包括60,000个的训练集样本，以及10,000个测试集样本.

PyTorch: Softmax多分类实战操作

其中:

train-images-idx3-ubyte.gz (训练数据集图片) 。

train-labels-idx1-ubyte.gz （训练数据集标记类别）。

t10k-images-idx3-ubyte.gz: （测试数据集）。

t10k-labels-idx1-ubyte.gz（测试数据集标记类别）。

PyTorch: Softmax多分类实战操作

MNIST数据集是经典图像数据集，包括10个类别(0到9)。每一张图片拉成向量表示，如下图784维向量作为第一层输入特征.

PyTorch: Softmax多分类实战操作

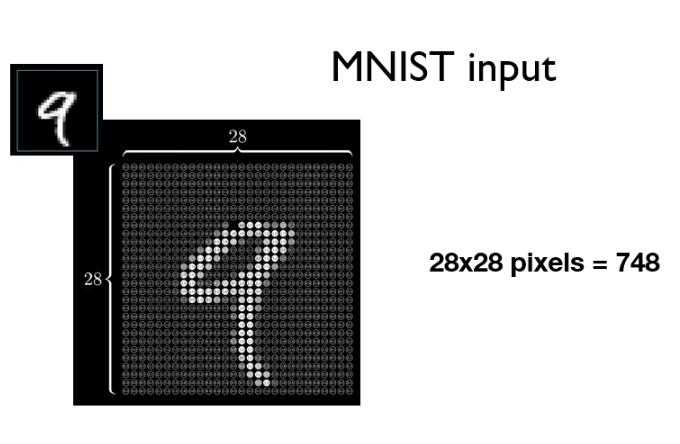
Softmax分类。

softmax函数的本质就是将一个K 维的任意实数向量压缩（映射）成另一个K维的实数向量，其中向量中的每个元素取值都介于（0，1）之间，并且压缩后的K个值相加等于1(变成了概率分布)。在选用Softmax做多分类时，可以根据值的大小来进行多分类的任务，如取权重最大的一维。softmax介绍和公式网上很多，这里不介绍了。下面使用Pytorch定义一个多层网络(4个隐藏层，最后一层softmax概率归一化)，输出层为10正好对应10类.

PyTorch: Softmax多分类实战操作

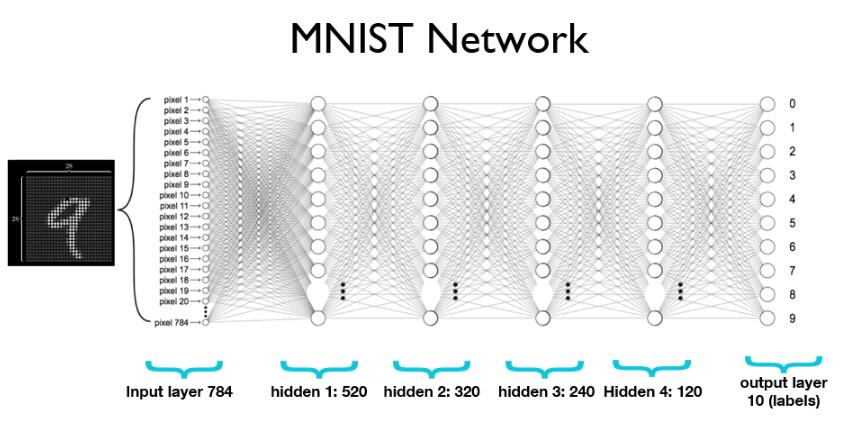
PyTorch实战。

 
    ? 
   
 
     
       
       
         import 
         torch 
        
 
         import 
         torch.nn as nn 
        
 
         import 
         torch.nn.functional as F 
        
 
         import 
         torch.optim as optim 
        
 
         from 
         torchvision  
         import 
         datasets, transforms 
        
 
         from 
         torch.autograd  
         import 
         Variable 
        

            
        
 
         # Training settings 
        
 
         batch_size  
         = 
         64 
        

            
        
 
         # MNIST Dataset 
        
 
         train_dataset  
         = 
         datasets.MNIST(root 
         = 
         './mnist_data/' 
         , 
        
 
                          
         train 
         = 
         True 
         , 
        
 
                          
         transform 
         = 
         transforms.ToTensor(), 
        
 
                          
         download 
         = 
         True 
         ) 
        

            
        
 
         test_dataset  
         = 
         datasets.MNIST(root 
         = 
         './mnist_data/' 
         , 
        
 
                         
         train 
         = 
         False 
         , 
        
 
                         
         transform 
         = 
         transforms.ToTensor()) 
        

            
        
 
         # Data Loader (Input Pipeline) 
        
 
         train_loader  
         = 
         torch.utils.data.DataLoader(dataset 
         = 
         train_dataset, 
        
 
                                
         batch_size 
         = 
         batch_size, 
        
 
                                
         shuffle 
         = 
         True 
         ) 
        

            
        
 
         test_loader  
         = 
         torch.utils.data.DataLoader(dataset 
         = 
         test_dataset, 
        
 
                               
         batch_size 
         = 
         batch_size, 
        
 
                               
         shuffle 
         = 
         False 
         ) 
        
 
         class 
         Net(nn.Module): 
        
 
            
         def 
         __init__( 
         self 
         ): 
        
 
              
         super 
         (Net,  
         self 
         ).__init__() 
        
 
              
         self 
         .l1  
         = 
         nn.Linear( 
         784 
         ,  
         520 
         ) 
        
 
              
         self 
         .l2  
         = 
         nn.Linear( 
         520 
         ,  
         320 
         ) 
        
 
              
         self 
         .l3  
         = 
         nn.Linear( 
         320 
         ,  
         240 
         ) 
        
 
              
         self 
         .l4  
         = 
         nn.Linear( 
         240 
         ,  
         120 
         ) 
        
 
              
         self 
         .l5  
         = 
         nn.Linear( 
         120 
         ,  
         10 
         ) 
        

            
        
 
            
         def 
         forward( 
         self 
         , x): 
        
 
              
         # Flatten the data (n, 1, 28, 28) --> (n, 784) 
        
 
              
         x  
         = 
         x.view( 
         - 
         1 
         ,  
         784 
         ) 
        
 
              
         x  
         = 
         F.relu( 
         self 
         .l1(x)) 
        
 
              
         x  
         = 
         F.relu( 
         self 
         .l2(x)) 
        
 
              
         x  
         = 
         F.relu( 
         self 
         .l3(x)) 
        
 
              
         x  
         = 
         F.relu( 
         self 
         .l4(x)) 
        
 
              
         return 
         F.log_softmax( 
         self 
         .l5(x), dim 
         = 
         1 
         ) 
        
 
              
         #return self.l5(x) 
        
 
         model  
         = 
         Net() 
        
 
         optimizer  
         = 
         optim.SGD(model.parameters(), lr 
         = 
         0.01 
         , momentum 
         = 
         0.5 
         ) 
        
 
         def 
         train(epoch): 
        

            
        
 
            
         # 每次输入barch_idx个数据 
        
 
            
         for 
         batch_idx, (data, target)  
         in 
         enumerate 
         (train_loader): 
        
 
              
         data, target  
         = 
         Variable(data), Variable(target) 
        

            
        
 
              
         optimizer.zero_grad() 
        
 
              
         output  
         = 
         model(data) 
        
 
              
         # loss 
        
 
              
         loss  
         = 
         F.nll_loss(output, target) 
        
 
              
         loss.backward() 
        
 
              
         # update 
        
 
              
         optimizer.step() 
        
 
              
         if 
         batch_idx  
         % 
         200 
         = 
         = 
         0 
         : 
        
 
                
         print 
         ( 
         'Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}' 
         . 
         format 
         ( 
        
 
                  
         epoch, batch_idx  
         * 
         len 
         (data),  
         len 
         (train_loader.dataset), 
        
 
                  
         100. 
         * 
         batch_idx  
         / 
         len 
         (train_loader), loss.data[ 
         0 
         ])) 
        
 
         def 
         test(): 
        
 
            
         test_loss  
         = 
         0 
        
 
            
         correct  
         = 
         0 
        
 
            
         # 测试集 
        
 
            
         for 
         data, target  
         in 
         test_loader: 
        
 
              
         data, target  
         = 
         Variable(data, volatile 
         = 
         True 
         ), Variable(target) 
        
 
              
         output  
         = 
         model(data) 
        
 
              
         # sum up batch loss 
        
 
              
         test_loss  
         + 
         = 
         F.nll_loss(output, target).data[ 
         0 
         ] 
        
 
              
         # get the index of the max 
        
 
              
         pred  
         = 
         output.data. 
         max 
         ( 
         1 
         , keepdim 
         = 
         True 
         )[ 
         1 
         ] 
        
 
              
         correct  
         + 
         = 
         pred.eq(target.data.view_as(pred)).cpu(). 
         sum 
         () 
        

            
        
 
            
         test_loss  
         / 
         = 
         len 
         (test_loader.dataset) 
        
 
            
         print 
         ( 
         '\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n' 
         . 
         format 
         ( 
        
 
              
         test_loss, correct,  
         len 
         (test_loader.dataset), 
        
 
              
         100. 
         * 
         correct  
         / 
         len 
         (test_loader.dataset))) 
        

            
        
 
         for 
         epoch  
         in 
         range 
         ( 
         1 
         , 
         6 
         ): 
        
 
            
         train(epoch) 
        
 
            
         test() 
        

            
        
 
         输出结果： 
        
 
         Train Epoch:  
         1 
         [ 
         0 
         / 
         60000 
         ( 
         0 
         % 
         )]   Loss:  
         2.292192 
        
 
         Train Epoch:  
         1 
         [ 
         12800 
         / 
         60000 
         ( 
         21 
         % 
         )]  Loss:  
         2.289466 
        
 
         Train Epoch:  
         1 
         [ 
         25600 
         / 
         60000 
         ( 
         43 
         % 
         )]  Loss:  
         2.294221 
        
 
         Train Epoch:  
         1 
         [ 
         38400 
         / 
         60000 
         ( 
         64 
         % 
         )]  Loss:  
         2.169656 
        
 
         Train Epoch:  
         1 
         [ 
         51200 
         / 
         60000 
         ( 
         85 
         % 
         )]  Loss:  
         1.561276 
        

            
        
 
         Test  
         set 
         : Average loss:  
         0.0163 
         , Accuracy:  
         6698 
         / 
         10000 
         ( 
         67 
         % 
         ) 
        

            
        
 
         Train Epoch:  
         2 
         [ 
         0 
         / 
         60000 
         ( 
         0 
         % 
         )]   Loss:  
         0.993218 
        
 
         Train Epoch:  
         2 
         [ 
         12800 
         / 
         60000 
         ( 
         21 
         % 
         )]  Loss:  
         0.859608 
        
 
         Train Epoch:  
         2 
         [ 
         25600 
         / 
         60000 
         ( 
         43 
         % 
         )]  Loss:  
         0.499748 
        
 
         Train Epoch:  
         2 
         [ 
         38400 
         / 
         60000 
         ( 
         64 
         % 
         )]  Loss:  
         0.422055 
        
 
         Train Epoch:  
         2 
         [ 
         51200 
         / 
         60000 
         ( 
         85 
         % 
         )]  Loss:  
         0.413933 
        

            
        
 
         Test  
         set 
         : Average loss:  
         0.0065 
         , Accuracy:  
         8797 
         / 
         10000 
         ( 
         88 
         % 
         ) 
        

            
        
 
         Train Epoch:  
         3 
         [ 
         0 
         / 
         60000 
         ( 
         0 
         % 
         )]   Loss:  
         0.465154 
        
 
         Train Epoch:  
         3 
         [ 
         12800 
         / 
         60000 
         ( 
         21 
         % 
         )]  Loss:  
         0.321842 
        
 
         Train Epoch:  
         3 
         [ 
         25600 
         / 
         60000 
         ( 
         43 
         % 
         )]  Loss:  
         0.187147 
        
 
         Train Epoch:  
         3 
         [ 
         38400 
         / 
         60000 
         ( 
         64 
         % 
         )]  Loss:  
         0.469552 
        
 
         Train Epoch:  
         3 
         [ 
         51200 
         / 
         60000 
         ( 
         85 
         % 
         )]  Loss:  
         0.270332 
        

            
        
 
         Test  
         set 
         : Average loss:  
         0.0045 
         , Accuracy:  
         9137 
         / 
         10000 
         ( 
         91 
         % 
         ) 
        

            
        
 
         Train Epoch:  
         4 
         [ 
         0 
         / 
         60000 
         ( 
         0 
         % 
         )]   Loss:  
         0.197497 
        
 
         Train Epoch:  
         4 
         [ 
         12800 
         / 
         60000 
         ( 
         21 
         % 
         )]  Loss:  
         0.234830 
        
 
         Train Epoch:  
         4 
         [ 
         25600 
         / 
         60000 
         ( 
         43 
         % 
         )]  Loss:  
         0.260302 
        
 
         Train Epoch:  
         4 
         [ 
         38400 
         / 
         60000 
         ( 
         64 
         % 
         )]  Loss:  
         0.219375 
        
 
         Train Epoch:  
         4 
         [ 
         51200 
         / 
         60000 
         ( 
         85 
         % 
         )]  Loss:  
         0.292754 
        

            
        
 
         Test  
         set 
         : Average loss:  
         0.0037 
         , Accuracy:  
         9277 
         / 
         10000 
         ( 
         93 
         % 
         ) 
        

            
        
 
         Train Epoch:  
         5 
         [ 
         0 
         / 
         60000 
         ( 
         0 
         % 
         )]   Loss:  
         0.183354 
        
 
         Train Epoch:  
         5 
         [ 
         12800 
         / 
         60000 
         ( 
         21 
         % 
         )]  Loss:  
         0.207930 
        
 
         Train Epoch:  
         5 
         [ 
         25600 
         / 
         60000 
         ( 
         43 
         % 
         )]  Loss:  
         0.138435 
        
 
         Train Epoch:  
         5 
         [ 
         38400 
         / 
         60000 
         ( 
         64 
         % 
         )]  Loss:  
         0.120214 
        
 
         Train Epoch:  
         5 
         [ 
         51200 
         / 
         60000 
         ( 
         85 
         % 
         )]  Loss:  
         0.266199 
        

            
        
 
         Test  
         set 
         : Average loss:  
         0.0026 
         , Accuracy:  
         9506 
         / 
         10000 
         ( 
         95 
         % 
         ) 
        
 
         Process finished with exit code  
         0 
        
 
     
 
   

随着训练迭代次数的增加，测试集的精确度还是有很大提高的。并且当迭代次数为5时，使用这种简单的网络可以达到95%的精确度.

以上这篇PyTorch: Softmax多分类实战操作就是小编分享给大家的全部内容了，希望能给大家一个参考，也希望大家多多支持我.

原文链接：https://blog.csdn.net/m0_37306360/article/details/79309849 。

最后此篇关于PyTorch: Softmax多分类实战操作的文章就讲到这里了,如果你想了解更多关于PyTorch: Softmax多分类实战操作的内容请搜索CFSDN的文章或继续浏览相关文章，希望大家以后支持我的博客！。

文章推荐： Django使用详解:ORM 的反向查找(related_name)

文章推荐： Python实现决策树C4.5算法的示例

文章推荐： python实现决策树ID3算法的示例代码

文章推荐：浅谈Django中的数据库模型类-models.py(一对一的关系)

java - Struts2 操作 > JSP > 操作
我正在努力做到这一点在我的操作中从数据库获取对象列表(确定) 在 JSP 上打印(确定) 此列表作为 JSP 中的可编辑表出现。我想修改然后将其提交回同一操作以将其保存在我的数据库中(失败。当我使用
linq - 不支持嵌套查询。操作 1 ='UnionAll' 操作 2 ='MultiStreamNest'
我有以下形式的 Linq to Entities 查询: var x = from a in SomeData where ... some conditions ... select
c# - 不支持嵌套查询。操作 1 ='UnionAll' 操作 2 ='MultiStreamNest'
我有以下查询。 var query = Repository.Query() .Where(p => !p.IsDeleted && p.Article.ArticleSections.Cou
java - Jtable ListSelectionListener 不响应 jtable 操作，而是响应同一个类中的另一个 jtable 操作
我正在编写一个应用程序包，其中包含一个主类，其中主方法与GUI类分开，GUI类包含一个带有jtabbedpane的jframe，它有两个选项卡，第一个选项卡包含一个jtable，称为jtable1，第
c# - LINQ 嵌套数组和三元运算符。不支持嵌套查询。操作 1 ='Case' 操作 2 ='Collect'
以下代码产生错误 The nested query is not supported. Operation1='Case' Operation2='Collect' 问题是我做错了什么？我该如何解决？
Redis哨兵中的C#操作
我已经为 HA redis 集群(2 个副本、1 个主节点、3 个哨兵)设置了本地 docker 环境。只有哨兵暴露端口(10021、10022、10023)。我使用的是 stackexchange
液体模板过滤器中的日期数学/操作
我正在 Desk.com 中构建一个“集成 URL”，它使用 Shopify Liquid 模板过滤器语法。对于开始日期为 7 天前而结束日期为现在的查询，此 URL 需要包含“开始日期”和“结束日期
Python为什么不支持 i++/i--操作
你一定想过。然而情况却不理想，python中只能使用类似于 i++/i--等操作。 python中的自增操作下面代码几乎是所有程序员在python中进行自增(减)操作的常用
GitHub 操作 - 将分支名称显示为构建名称
我需要在每个使用 github 操作的手动构建中显示分支。例如:https://gyazo.com/2131bf83b0df1e2157480e5be842d4fb 我应该显示分支而不是一个。最佳答
Perl qr//操作
我有一个关于 Perl qr 运算符的问题: #!/usr/bin/perl -w &mysplit("a:b:c", /:/); sub mysplit { my($str, $patt
uml - ArgoUML 操作
我已经使用 ArgoUML 创建了一个 ERD(实体关系图)，我希望在一个类中创建两个操作，它们都具有 void 返回类型。但是，我只能创建一个返回 void 类型的操作。例如: 我能够将 book
关于拉取请求和主分支的 Github 操作
Github 操作仍处于测试阶段并且很新，但我希望有人可以提供帮助。我认为可以在主分支和拉取请求上运行 github 操作，如下所示: on: pull_request push: b
用于记录的 Twilio 操作
我正在尝试创建一个 Twilio 工作流来调用电话并记录用户所说的内容。为此，我正在使用 Record，但我不确定要在 action 参数中放置什么。尽管我知道 Twilio 会发送有关调用该 UR
OpenGL 模板缓冲区 OR 操作？
我不确定这是否可行，但值得一试。我正在使用模板缓冲区来减少使用此算法的延迟渲染器中光体积的过度绘制(当相机位于体积之外时): 使用廉价的着色器，将深度测试设置为 LEQUAL 绘制背面，将它们标记在模
用于复制和重命名文件的 GitHub 操作
有没有聪明的方法来复制和重命名文件通过 GitHub 操作？我想将一些自述文件复制到 /docs文件夹(:= 同一个 repo，不是远程的!)，它们将根据它们的 frontmatter 重命名
PowerShell CSV 操作
我有一个 .csv 文件，其中第一列包含用户名。它们采用 FirstName LastName 的形式。我想获取 FirstName 并将 LastName 的第一个字符添加到它上面，然后删除空格。然
Sitecore - 操作 URL
Sitecore 根据 Sitecore 树中定义的项目名称生成 URL， http://samplewebsite/Pages/Sample Page 但我们的客户有兴趣降低所有 URL(页面/示例
单击按钮时的 Angularjs 操作
我正在尝试进行一些计算，但是一旦我输入金额，它就会完成。我只是希望通过单击按钮而不是自动发生这种情况。到目前为止我做了什么: Angular JS - programming-fr
将文件从一个存储库复制到另一个存储库的 github 操作
我的公司创建了一种在环境之间移动文件的复杂方法，现在我们希望将某些构建的 JS 文件(已转换和缩小)从一个 github 存储库移动到另一个。使用 github 操作可以实现这一点吗？最佳答案最简
java - JSONArray 操作
在我的代码中，我创建了一个 JSONArray 对象。并向 JSONArray 对象添加了两个 JSONObject。我使用的是 json-simple-1.1.jar。我的代码是 package j

qq735679552

个人简介

我是一名优秀的程序员,十分优秀！

作者热门文章

滴滴打车优惠券免费领取

全站热门文章

首页

博学

6Ren·AI

商城

PyTorch: Softmax多分类实战操作