使用keras实现Precise, Recall, F1-socre方式-6ren

使用keras实现Precise, Recall, F1-socre方式

转载作者：qq735679552 更新时间：2022-09-29 22:32:09

25

4

CFSDN坚持开源创造价值，我们致力于搭建一个资源共享平台，让每一个IT人在这里找到属于你的精彩世界.

这篇CFSDN的博客文章使用keras实现Precise, Recall, F1-socre方式由作者收集整理，如果你对这篇文章有兴趣，记得点赞哟.

实现过程。

 
    ? 
   
 
     
       
       
         from 
         keras  
         import 
         backend as K 
        
 
         def 
         Precision(y_true, y_pred): 
        
 
           
         """精确率""" 
        
 
           
         tp 
         = 
         K. 
         sum 
         (K. 
         round 
         (K.clip(y_true  
         * 
         y_pred,  
         0 
         ,  
         1 
         )))  
         # true positives 
        
 
           
         pp 
         = 
         K. 
         sum 
         (K. 
         round 
         (K.clip(y_pred,  
         0 
         ,  
         1 
         )))  
         # predicted positives 
        
 
           
         precision  
         = 
         tp 
         / 
         (pp 
         + 
         K.epsilon()) 
        
 
           
         return 
         precision 
        
 
           
        
 
         def 
         Recall(y_true, y_pred): 
        
 
           
         """召回率""" 
        
 
           
         tp  
         = 
         K. 
         sum 
         (K. 
         round 
         (K.clip(y_true  
         * 
         y_pred,  
         0 
         ,  
         1 
         )))  
         # true positives 
        
 
           
         pp  
         = 
         K. 
         sum 
         (K. 
         round 
         (K.clip(y_true,  
         0 
         ,  
         1 
         )))  
         # possible positives 
        
 
           
         recall  
         = 
         tp  
         / 
         (pp  
         + 
         K.epsilon()) 
        
 
           
         return 
         recall 
        
 
           
        
 
         def 
         F1(y_true, y_pred): 
        
 
           
         """F1-score""" 
        
 
           
         precision  
         = 
         Precision(y_true, y_pred) 
        
 
           
         recall  
         = 
         Recall(y_true, y_pred) 
        
 
           
         f1  
         = 
         2 
         * 
         ((precision  
         * 
         recall)  
         / 
         (precision  
         + 
         recall  
         + 
         K.epsilon())) 
        
 
           
         return 
         f1 
        
 
     
 
   

补充知识：分类问题的几个评价指标（Precision、Recall、F1-Score、Micro-F1、Macro-F1）。

四个基本概念。

TP、True Positive 真阳性：预测为正，实际也为正。

FP、False Positive 假阳性：预测为正，实际为负。

FN、False Negative 假阴性：预测与负、实际为正。

TN、True Negative 真阴性：预测为负、实际也为负.

【一致判真假，预测判阴阳。】。

以分类问题为例：（word公式为什么粘不过来？？头疼。）。

使用keras实现Precise, Recall, F1-socre方式

首先看真阳性：真阳性的定义是“预测为正，实际也是正”，这个最好理解，就是指预测正确，是哪个类就被分到哪个类。对类A而言，TP的个位数为2，对类B而言，TP的个数为2，对类C而言，TP的个数为1.

然后看假阳性，假阳性的定义是“预测为正，实际为负”，就是预测为某个类，但是实际不是。对类A而言，FP个数为0，我们预测之后，把1和2分给了A，这两个都是正确的，并不存在把不是A类的值分给A的情况。类B的FP是2，"3"和"8"都不是B类，但却分给了B，所以为假阳性。类C的假阳性个数为2.

最后看一下假阴性，假阴性的定义是“预测为负，实际为正”，对类A而言，FN为2，"3"和"4"分别预测为B和C，但是实际是A，也就是预测为负，实际为正。对类B而言，FN为1，对类C而言，FN为1.

具体情况看如下表格:

	A 。	B 。	C 。	总计。
TP 。	2 。	2 。	1 。	5 。
FP 。	0 。	2 。	2 。	4 。
FN 。	2 。	1 。	1 。	4 。

感谢这两位的指正。

使用keras实现Precise, Recall, F1-socre方式

精确率和召回率。

使用keras实现Precise, Recall, F1-socre方式

计算我们预测出来的某类样本中，有多少是被正确预测的。针对预测样本而言.

使用keras实现Precise, Recall, F1-socre方式

针对原先实际样本而言，有多少样本被正确的预测出来了.

套用网上的一个例子:

某池塘有1400条鲤鱼，300只虾，300只鳖。现在以捕鲤鱼为目的。撒一大网，逮着了700条鲤鱼，200只虾，100只鳖。那么，这些指标分别如下:

精确率 = 700 / (700 +200 + 100) = 70% 。

召回率 = 700 / 1400 =50% 。

可以吧上述的例子看成分类预测问题，对于“鲤鱼来说”，TP真阳性为700，FP假阳性为300，FN假阴性为700.

Precison=TP/(TP+FP)=700(700+300)=70% 。

Recall=TP/(TP+FN)=700/(700+700)=50% 。

将上述例子，改变一下：把池子里的所有的鲤鱼、虾和鳖都一网打尽，观察这些指标的变化.

精确率 = 1400 / (1400 +300 + 300) = 70% 。

召回率 = 1400 / 1400 =100% 。

TP为1400：有1400条鲤鱼被预测出来；FP为600：有600个生物不是鲤鱼类，却被归类到鲤鱼；FN为0，鲤鱼都被归类到鲤鱼类去了，并没有归到其他类.

Precision=TP/(TP+FP)=1400/(1400+600)=70% 。

Recall=TP/(TP+FN)=1400/(1400)=100% 。

其实就是分母不同，一个分母是预测为正的样本数，另一个是原来样本中所有的正样本数.

作为预测者，我们当然是希望，Precision和Recall都保持一个较高的水准，但事实上这两者在某些情况下有矛盾的。比如极端情况下，我们只搜索出了一个结果，且是正确的，那么Precision就是100%，但是Recall就很低；而如果我们把所有结果都返回，那么比如Recall是100%，但是Precision就会很低。因此在不同的场合中需要自己判断希望Precision比较高或是Recall比较高，此时我们可以引出另一个评价指标—F1-Score(F-Measure).

F1-Score 。

F1分数（F1 Score），是统计学中用来衡量二分类模型精确度的一种指标。它同时兼顾了分类模型的精确率和召回率。F1分数可以看作是模型精确率和召回率的一种加权平均，它的最大值是1，最小值是0。（出自百度百科）。

数学定义：F1分数（F1-Score），又称为平衡F分数（BalancedScore），它被定义为精确率和召回率的调和平均数.

使用keras实现Precise, Recall, F1-socre方式

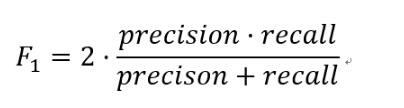
更一般的，我们定义Fβ分数为:

使用keras实现Precise, Recall, F1-socre方式

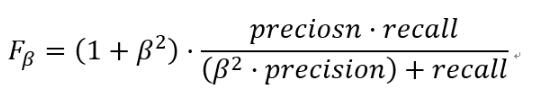
除了F1分数之外，F0.5分数和F2分数，在统计学中也得到了大量应用，其中，F2分数中，召回率的权重高于精确率，而F0.5分数中，精确率的权重高于召回率.

Micro-F1和Macro-F1 。

最后看Micro-F1和Macro-F1。在第一个多标签分类任务中，可以对每个“类”，计算F1，显然我们需要把所有类的F1合并起来考虑.

这里有两种合并方式:

第一种计算出所有类别总的Precision和Recall，然后计算F1.

例如依照最上面的表格来计算:Precison=5/(5+4)=0.556,Recall=5/(5+4)=0.556，然后带入F1的公式求出F1，这种方式被称为Micro-F1微平均.

第二种方式是计算出每一个类的Precison和Recall后计算F1，最后将F1平均.

例如上式A类：P=2/(2+0)=1.0，R=2/(2+2)=0.5，F1=(2*1*0.5)/1+0.5=0.667。同理求出B类C类的F1，最后求平均值，这种范式叫做Macro-F1宏平均.

本篇完，如有错误，还望指正。以上这篇使用keras实现Precise, Recall, F1-socre方式就是小编分享给大家的全部内容了，希望能给大家一个参考，也希望大家多多支持我.

原文链接：https://blog.csdn.net/joleoy/article/details/85787457 。

最后此篇关于使用keras实现Precise, Recall, F1-socre方式的文章就讲到这里了,如果你想了解更多关于使用keras实现Precise, Recall, F1-socre方式的内容请搜索CFSDN的文章或继续浏览相关文章，希望大家以后支持我的博客！。

25

4

0

文章推荐：基于python和flask实现http接口过程解析

文章推荐：阴阳师妖怪屋山兔阵容怎么搭配山兔阵容搭配详解

文章推荐： Android在listview添加checkbox实现原理与代码

文章推荐： python实现将pvr格式转换成pvr.ccz的方法

c - 在英特尔 x64 汇编中执行函数的最快(CPU 方式)方式？
我一直在阅读有关汇编函数的内容，但对于是使用进入和退出还是仅使用调用/返回指令来快速执行，我感到很困惑。一种方式快而另一种方式更小吗？例如，在不内联函数的情况下，在汇编中执行此操作的最快(stdcal
解析元组的 Pythonic 方式
我正在处理一个元组列表，如下所示: res = [('stori', 'JJ'), ('man', 'NN'), ('unnatur', 'JJ'), ('feel', 'NN'), ('pig',
使用线程的 Pythonic 方式
最近我一直在做很多网络或 IO 绑定(bind)操作，使用线程有助于加快代码速度。我注意到我一直在一遍又一遍地编写这样的代码: threads = [] for machine, user, data
请求资源子集的 RESTful 方式
假设我有一个名为 user_stats 的资源，其中包含用户拥有的帖子、评论、喜欢和关注者的数量。是否有一种 RESTful 方式只询问该统计数据的一部分(即，对于 user_stats/3，请告诉我
接受选择的 RESTful 方式
我有一个简单的 api，它的工作原理是这样的: 用户创建一个请求 ( POST /requests ) 另一个用户检索所有请求 ( GET /requests ) 然后向请求添加报价 ( POST /
扩展构建器模式的 Pythonic 方式
考虑以下 CDK Python 中的示例(对于这个问题，不需要 AWS 知识，这应该对基本上任何构建器模式都有效，我只是在这个示例中使用 CDK，因为我使用这个库遇到了这个问题。): from aws
用于管理对象池的 Scala 方式
Scala 中管理对象池的首选方法是什么？我需要单线程创建和删除大规模对象(不需要同步)。在 C++ 中，我使用了静态对象数组。在 Scala 中处理它的惯用和有效方法是什么？最佳答案我会把它
将多个类方法应用于对象列表的 Pythonic 方式
我有一个带有一些内置方法的类。这是该类的抽象示例: class Foo: def __init__(self): self.a = 0 self.b = 0
返回和检查方法执行的 Pythonic 方式
返回和检查方法执行的 Pythonic 方式我目前在 python 代码中使用 golang 编码风格，决定移动 pythonic 方式例子: import sys from typing imp
处理丢失数据的 RESTful 方式
我正在开发一个 RESTful API。其中一个 URL 允许调用者通过 id 请求特定人员的记录。返回该 id 不存在的记录的常规值是什么？服务器是否应该发回一个空对象或者一个 404，或者其他什
加载具有相似文件名的文件的 Pythonic 方式
我正在使用 pathlib.Path() 检查文件是否存在，并使用 rasterio 将其作为图像打开. filename = pathlib.Path("./my_file-name.tif") 但
创建嵌套字典的 Pythonic 方式
我正在寻找一种 Pythonic 方式来从列表和字典创建嵌套字典。以下两个语句产生相同的结果: a = [3, 4] b = {'a': 1, 'b': 2} c = dict(zip(b, a))
处理异常后恢复的 Pythonic 方式
我有一个正在操裁剪理设备的脚本。设备有时会发生物理故障，当它发生时，我想重置设备并继续执行脚本。我有这个: while True: do_device_control() device
做组合别名的 Pythonic 方式
做组合别名的最pythonic和正确的方法是什么？这是一个假设的场景: class House: def cleanup(self, arg1, arg2, kwarg1=False):
在一个请求中创建多个项目的 RESTful 方式
我正在开发一个小型客户端服务器程序来收集订单。我想以“REST(ful)方式”来做到这一点。我想做的是: 收集所有订单行(产品和数量)并将完整订单发送到服务器目前我看到有两种选择: 将每个订单行发
动态调用静态方法的 Groovy 方式
我知道在 Groovy 中您可以使用字符串调用类/对象上的方法。例如: Foo."get"(1) /* or */ String meth = "get" Foo."$meth"(1) 有没有办法
复制没有不同属性的字典的 Pythonic 方式
在 ECMAScript6 中，您可以使用扩展运算符来解构这样的对象 const {a, ...rest} = obj; 它将 obj 浅拷贝到 rest，不带属性 a。有没有一种干净的方法可以在
函数中条件返回的 Pythonic 方式
我有几个函数返回数字或None。我希望我的包装函数返回第一个不是 None 的结果。除了下面的方法之外，还有其他方法吗？ def func1(): return None def func2(
处理资源之间双向关系的 RESTful 方式
假设我想设计一个 REST api 来讨论歌曲、专辑和艺术家(实际上我就是这样做的，就像我之前的 1312414 个人一样)。歌曲资源始终与其所属专辑相关联。相反，专辑资源与其包含的所有歌曲相关联。
有条件地使用上下文管理器的 Pythonic 方式
这是我认为必须经常出现的问题，但我一直无法找到一个好的解决方案。假设我有一个函数，它可以作为参数传递一个开放资源(如文件或数据库连接对象)，或者需要自己创建一个。如果函数需要自己打开文件，最佳实践通常

首页

博学

6Ren·AI

商城

使用keras实现Precise, Recall, F1-socre方式