- ubuntu12.04环境下使用kvm ioctl接口实现最简单的虚拟机
- Ubuntu 通过无线网络安装Ubuntu Server启动系统后连接无线网络的方法
- 在Ubuntu上搭建网桥的方法
- ubuntu 虚拟机上网方式及相关配置详解
CFSDN坚持开源创造价值,我们致力于搭建一个资源共享平台,让每一个IT人在这里找到属于你的精彩世界.
这篇CFSDN的博客文章利用Python暴力破解zip文件口令的方法详解由作者收集整理,如果你对这篇文章有兴趣,记得点赞哟.
前言 。
通过Python内置的zipfile模块实现对zip文件的解压,加点料完成口令破解 。
zipfile模块用来做zip格式编码的压缩和解压缩的,zipfile里有两个非常重要的class, 分别是ZipFile和ZipInfo, 在绝大多数的情况下,我们只需要使用这两个class就可以了。ZipFile是主要的类,用来创建和读取zip文件而ZipInfo是存储的zip文件的每个文件的信息的.
比如要读取一个Python zipfile 模块,这里假设filename是一个文件的路径
|
1
2
3
4
|
import
zipfile
z
=
zipfile.ZipFile(filename,
'r'
)
for
i
in
z.infolist():
print
i.file_size, i.header_offset
|
这里使用了z.infolist(), 它返回的就是压缩包内所有文件的信息,就是一个ZipInfo的列表。一个ZipInfo对象中包含了压缩包内一个文件的信息,其中比较常用的是 filename, file_size, header_offset, 分别为文件名,文件大小,文件数据在压缩包中的偏移.
准备阶段 。
首先你需要一个压缩文件,并且给它加上密码,样子长成这样 。
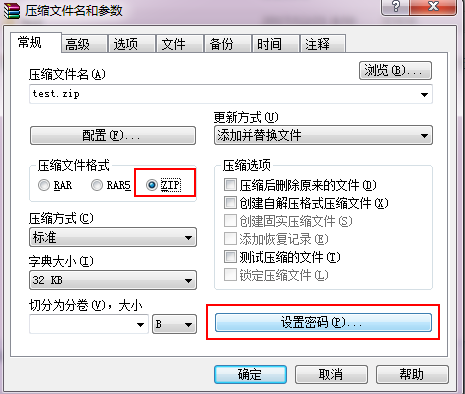
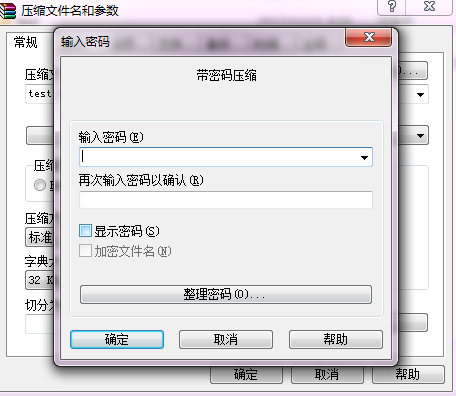
然后你就成功Get了一个自带密码的压缩文件,好了,这就结束了 。
暴力破解 。
首先我们先知道下什么是暴力破解,其实简单粗暴点来说,就是通过轮循的方式比对,我们一定都知道MD5加密,那么MD5是不可逆的,那网上那些所谓的MD5解密的网站是怎么做到的,其实也是暴力破解的方式.
举个栗子,你通过MD5加密了一段字符串 str="abc" 加密后的结果为 "3cd24fb0d6963f7d" 这么一长串别人肯定看不懂,MD5解密网站怎么做的,他们自己没事干的时候开始瞎试,把aa/cc/bb/abc 啥的都开始用MD5加密一遍,存到自己的数据库里,当你去查询的时候,他们会根据你提供的 "3cd24fb0d6963f7d" 在数据库里面比对,如果巧合的话就能找不到,大部分情况你的加密字符串稍微复杂点都找不到,这就是所谓的MD5解密,也就是暴力破解了 。
上代码 。
|
1
2
3
4
5
|
import
zipfile
#导入模块,它是做压缩和解压缩的
password
=
"123"
#我们设定的口令
zfile
=
zipfile.ZipFile(
"test.zip"
)
#要解压缩的压缩包
zfile.extractall(path
=
'C:\\Users\\Administrator\\Desktop\\', members=zfile.namelist(), pwd=password.encode('
utf
-
8
'))
#进行解压缩操作,path为输出的路径
|
我们运行一下上面的代码(当然你的加密口令要为123),会发现在桌面上已经把test.zip解压出来了,完美ending,不对还差一个暴力破解呢,自己知道密码还要破解啥有用,别着急,继续往下看 。
|
1
2
3
4
5
6
7
8
9
10
|
import
zipfile
zfile
=
zipfile.ZipFile(
"test.zip"
)
passFile
=
open
(
'pwd.txt'
)
#读取你设定的密码文件
for
line
in
passFile.readlines():
try
:
password
=
line.strip(
'\n'
)
zfile.extractall(path
=
'C:\\Users\\Administrator\\Desktop\\', members=zfile.namelist(), pwd=password.encode('
utf
-
8
'))
break
except
:
print
(
"又错了"
)
|
pwd.txt里面内容如下 。
|
1
2
3
4
|
1223
abc
aaa
123
|
好了,这就完成了zip文件口令的暴力破解,其实只是很巧妙的利用了try except异常机制,当解压正常的时候就正常密码正常,解压失败会报出异常,动手试试 。
总结 。
以上就是这篇文章的全部内容了,希望本文的内容对大家的学习或者工作具有一定的参考学习价值,如果有疑问大家可以留言交流,谢谢大家对我的支持.
原文链接:https://segmentfault.com/a/1190000012519264 。
最后此篇关于利用Python暴力破解zip文件口令的方法详解的文章就讲到这里了,如果你想了解更多关于利用Python暴力破解zip文件口令的方法详解的内容请搜索CFSDN的文章或继续浏览相关文章,希望大家以后支持我的博客! 。
在后台开启了“URL Rewrite”,看起来一切正常,可是点击某一栏目的时候却怎么都进不去,显示的依然是论坛的首页。看了一下论坛目录下,原来这下面并没有自己的.htaccess文件,所以默认使用的
本文实例为大家分享了.net发送邮件的实现代码,供大家参考,具体内容如下 关键代码: 需要引用命名空间: using System.Net.Mail; using System.Net;
今天的一个小测试是老师让用.NET用控件来制作一个拉菜单要求如下: 将鼠标移到父菜单上弹出3个子菜单,而且每个子菜单都有超链接。 以下是我自己做的代码: 复制代
我有以下内容 static const unsigned int chromosome = 6; double bestFitness[chromosomes]; for(int i = 0; i
关于附图,我需要一个计算算法来将 A 轴向下移动 n 英寸,将 B 轴从左向右移动 m 英寸,以便组件圆 D 遵循抛物线的曲线;圆 D 并不总是 10 英寸,可以更小。我不是数学专业的,所以这对我来说
我正在尝试利用我的格式字符串错误,它存在于这个程序中: #include #include #include #include #include void foo(char* tmp, ch
用Matplotlib和Seaborn这类Python库可以画出很好看的图,但是这些图只是静态的,难以动态且美观地呈现数值变化。要是在你下次的演示、视频、社交媒体Po文里能用短视频呈现数据变化,是不
1、进程介绍 进程:正在执行的程序,由程序、数据和进程控制块组成,是正在执行的程序,程序的一次执行过程,是资源调度的基本单位。 程序:没有执行的代码,是一个静态的。 2、线程
1、前言 在开发过程中,有时会遇到需要控制任务并发执行数量的需求。 例如一个爬虫程序,可以通过限制其并发任务数量来降低请求频率,从而避免由于请求过于频繁被封禁问题的发生。 接下来
Opera 管理着一个漏洞赏金计划,研究人员可以在该计划中报告 Opera 软件中的漏洞并获得奖励。 这篇文章就是我发现的一个漏洞——网页可能会从用户那里检索本地文件的屏幕截图。 考虑到 O
C++ 文件查找 在C++中我们要如何查找文件呢?我们需要一个结构体和几个大家可能不太熟悉的函数。这些函数和结构体在的头文件中,结构体为struct _finddata_t ,函数为_findfi
1、前言 本文利用 fsockopen() 函数,编写一个功能简单的端口扫描器。 2、关键技术 本实例的端口号是固定的,通过对数组的遍历,利用 fsockopen() 函数连接,如果连接成功,
最近在将一些项目的rest api迁移到.net core中,最开始是用的Nginx做反向代理,将已经完成切换的部分切入系统,如下图所示: 由于迁移过程中也在进行代码重构,需要经常比较频繁的测
前言 最近学习了python,感觉挺多地方能用到它的。打包 测试 上传 爬电影....而且代码量是真少。人生苦短,我用python。而今天写的这个是因为下载电影时总会发现除了视频还会有这两个文件,
1、Monkey测试简介 Monkey测试是Android平台自动化测试的一种手段,通过Monkey程序模拟用户触摸屏幕、滑动Trackball、按键等操作来对设备上的程序进行压力测试,检测程序
一直想写一套生成静态页面的文章系统 但面对生成静态后的一些复杂数据库交互问题。又望而却步! 于是就想 有没有 在不耽误数据交互的情况下,而又能降低服务器负
Qt 利用大量第 3 方库进行图像编码、压缩、加密、音频和视频编解码器支持等。 从历史上看,当我想使用它们时,我总是必须将它们作为附加依赖项包含在内。我一直想知道是否有一种方法可以简单地重用 Qt 已
我想知道是否可以使用属性将功能“混合”到类/方法/属性中。 就像是: [TrackChanges] public Foo { get; set; } 如果可能的话,有谁会如何实现? 最佳答
有些站点位于共享主机(Windows 2003 Server)上,因此我无法访问服务器配置。 我到处都读到关于杠杆浏览器缓存的信息,特别是静态文件(jpg,css,js等)的信息,但是...在我的情况
我想在我的项目中使用 Julia 的主要原因之一是它的速度,尤其是在计算积分方面。 我想在某个区间 [a,b] 上积分一维函数 f(x)。一般来说,Julia 的 quadgk 函数将是一个快速而准确

我是一名优秀的程序员,十分优秀!