- ubuntu12.04环境下使用kvm ioctl接口实现最简单的虚拟机
- Ubuntu 通过无线网络安装Ubuntu Server启动系统后连接无线网络的方法
- 在Ubuntu上搭建网桥的方法
- ubuntu 虚拟机上网方式及相关配置详解
CFSDN坚持开源创造价值,我们致力于搭建一个资源共享平台,让每一个IT人在这里找到属于你的精彩世界.
这篇CFSDN的博客文章Python深度学习神经网络基本原理由作者收集整理,如果你对这篇文章有兴趣,记得点赞哟.
。




。
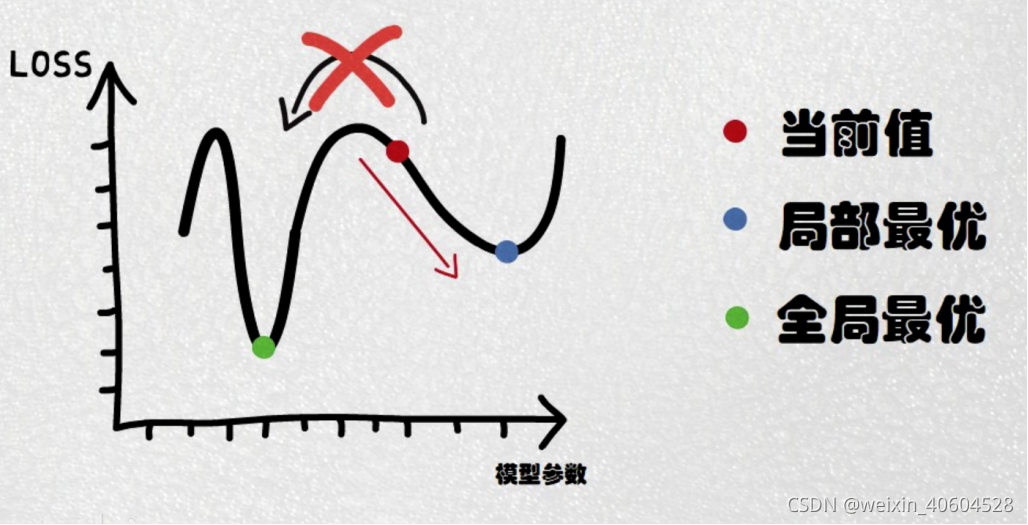
在详细了解梯度下降的算法之前,我们先看看相关的一些概念.
1. 步长(Learning rate):步长决定了在梯度下降迭代的过程中,每一步沿梯度负方向前进的长度。用上面下山的例子,步长就是在当前这一步所在位置沿着最陡峭最易下山的位置走的那一步的长度.
2.特征(feature):指的是样本中输入部分,比如2个单特征的样本(x(0),y(0)),(x(1),y(1))(x(0),y(0)),(x(1),y(1)),则第一个样本特征为x(0)x(0),第一个样本输出为y(0)y(0).
3. 假设函数(hypothesis function):在监督学习中,为了拟合输入样本,而使用的假设函数,记为hθ(x)hθ(x)。比如对于单个特征的m个样本(x(i),y(i))(i=1,2,...m)(x(i),y(i))(i=1,2,...m),可以采用拟合函数如下: hθ(x)=θ0+θ1xhθ(x)=θ0+θ1x.
4. 损失函数(loss function):为了评估模型拟合的好坏,通常用损失函数来度量拟合的程度。损失函数极小化,意味着拟合程度最好,对应的模型参数即为最优参数。在线性回归中,损失函数通常为样本输出和假设函数的差取平方。比如对于m个样本(xi,yi)(i=1,2,...m)(xi,yi)(i=1,2,...m),采用线性回归,损失函数为:
J(θ0,θ1)=∑i=1m(hθ(xi)−yi)2J(θ0,θ1)=∑i=1m(hθ(xi)−yi)2 。
其中xixi表示第i个样本特征,yiyi表示第i个样本对应的输出,hθ(xi)hθ(xi)为假设函数.



分享人:张娇娟 。
到此这篇关于Python深度学习神经网络基本原理的文章就介绍到这了,更多相关Python 神经网络内容请搜索我以前的文章或继续浏览下面的相关文章希望大家以后多多支持我! 。
原文链接:https://blog.csdn.net/weixin_40604528/article/details/120803080 。
最后此篇关于Python深度学习神经网络基本原理的文章就讲到这里了,如果你想了解更多关于Python深度学习神经网络基本原理的内容请搜索CFSDN的文章或继续浏览相关文章,希望大家以后支持我的博客! 。
我正在使用python 2.7 当我尝试在其上运行epsilon操作时出现此错误, 这是我的代码 import cv2 import numpy as np img = cv2.imread('img
1 很多程序员对互联网行业中广泛讨论的“35岁危机”表示不满,似乎所有的程序员都有着35岁的职业保质期。然而,随着AI技术的兴起,这场翻天覆地的技术革命正以更加残酷且直接的方式渗透到各行各业。程序员
我有一个包含多个子模块的项目,我想列出每个子模块的相对深度 该项目: main_project submodule1 submodule1\submodule1_1 submo
我有一张彩色图像及其深度图,它们都是由 Kinect 捕获的。我想将它投影到另一个位置(以查看它在另一个视角下的样子)。由于我没有 Kinect 的内在参数(相机参数);我该如何实现? P.S:我正在
给出了这三个网址: 1) https://example.com 2) https://example.com/app 3) https://example.com/app?param=hello 假
这个着色器(最后的代码)使用 raymarching 来渲染程序几何: 但是,在图像(上图)中,背景中的立方体应该部分遮挡粉红色实体;不是因为这个: struct fragmentOutput {
我希望能够在 ThreeJS 中创建一个房间。这是我到目前为止所拥有的: http://jsfiddle.net/7oyq4yqz/ var camera, scene, renderer, geom
我正在尝试通过编写小程序来学习 Haskell...所以我目前正在为简单表达式编写一个词法分析器/解析器。 (是的,我可以使用 Alex/Happy...但我想先学习核心语言)。 我的解析器本质上是一
我想使用像 [parse_ini_file][1] 这样的东西。 例如,我有一个 boot.ini 文件,我将加载该文件以进行进一步的处理: ;database connection sett
我正在使用 Mockito 来测试我的类(class)。我正在尝试使用深度 stub ,因为我没有办法在 Mockito 中的另一个模拟对象中注入(inject) Mock。 class MyServ
我试图在调整设备屏幕大小时重新排列布局,所以我这样做: if(screenOrientation == SCREEN_ORIENTATION_LANDSCAPE) { document
我正在 Ubuntu 上编写一个简单的 OpenGL 程序,它使用顶点数组绘制两个正方形(一个在另一个前面)。由于某种原因,GL_DEPTH_TEST 似乎不起作用。后面的物体出现在前面的物体前面
static FAST_FUNC int fileAction(const char *pathname, struct stat *sb UNUSED_PARAM, void *mo
我有这样的层次结构: namespace MyService{ class IBase { public: virtual ~IBase(){} protected: IPointer
我正在制作一个图片库,需要一些循环类别方面的帮助。下一个深度是图库配置文件中的已知设置,因此这不是关于无限深度循环的问题,而是循环已知深度并输出所有结果的最有效方法。 本质上,我想创建一个 包含系统中
如何以编程方式在树状结构上获取 n 深度迭代器?在根目录中我有 List 每个节点有 Map> n+1 深度。 我已修复 1 个深度: // DEPTH 1 nodeData.forEach(base
我正在构建一个包含大量自定义元素的 Polymer 单页界面。 现在我希望我的元素具有某种主样式,我可以在 index.html 或我的主要内容元素中定义它。可以这样想: index.html
我正在尝试每 25 秒连接到配对的蓝牙设备,通过 AlarmManager 安排,它会触发 WakefulBroadcastReceiver 以启动服务以进行连接。设备进入休眠状态后,前几个小时一切正
假设有一个有默认值的函数: int foo(int x=42); 如果这被其他人这样调用: int bar(int x=42) { return foo(x); } int moo(int x=42)
是否可以使用 Javascript 获取 url 深度(级别)? 如果我有这个网址:www.website.com/site/product/category/item -> depth=4www.w

我是一名优秀的程序员,十分优秀!