CFSDN坚持开源创造价值，我们致力于搭建一个资源共享平台，让每一个IT人在这里找到属于你的精彩世界.

这篇CFSDN的博客文章详解R语言MCMC:Metropolis-Hastings采样用于回归的贝叶斯估计由作者收集整理，如果你对这篇文章有兴趣，记得点赞哟.

MCMC是从复杂概率模型中采样的通用技术.

1. 蒙特卡洛
2. 马尔可夫链
3. Metropolis-Hastings算法

  。

问题

如果需要计算有复杂后验pdf p（θ| y）的随机变量θ的函数f（θ）的平均值或期望值.

您可能需要计算后验概率分布p（θ）的最大值.

解决期望值的一种方法是从p（θ）绘制N个随机样本，当N足够大时，我们可以通过以下公式逼近期望值或最大值 。

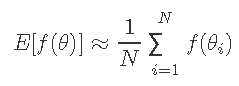
将相同的策略应用于通过从p（θ| y）采样并取样本集中的最大值来找到argmaxp（θ| y）.

---

  。

解决方法

1.1直接模拟 。

1.2逆CDF 。

1.3拒绝/接受抽样 。

如果我们不知道精确/标准化的pdf或非常复杂，则MCMC会派上用场.

---

  。

马尔可夫链

为了模拟马尔可夫链，我们必须制定一个过渡核T（xi，xj）。过渡核是从状态xi迁移到状态xj的概率.

马尔可夫链的收敛性意味着它具有平稳分布π。马尔可夫链的统计分布是平稳的,那么它意味着分布不会随着时间的推移而改变.

  。

Metropolis算法

对于一个Markov链是平稳的。基本上表示 。

处于状态x并转换为状态x'的概率必须等于处于状态x'并转换为状态x的概率 。

或者 。

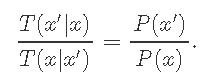
方法是将转换分为两个子步骤；候选和接受拒绝.

令q（x'| x）表示候选密度，我们可以使用概率α（x'| x）来调整q .

候选分布Q（X'| X）是给定的候选X的状态X'的条件概率， 。

和接受分布α（x'| x）的条件概率接受候选的状态X'-X'。我们设计了接受概率函数，以满足详细的平衡.

该转移概率可以写成:

插入上一个方程式，我们有 。

  。

Metropolis-Hastings算法

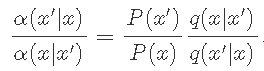
A的选择遵循以下逻辑.

在q下从x到x'的转移太频繁了。因此，我们应该选择α（x | x'）=1。但是，为了满足细致平稳，我们有 。

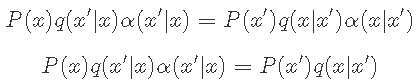
下一步是选择满足上述条件的接受。Metropolis-Hastings是一种常见的选择:

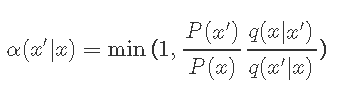
即，当接受度大于1时，我们总是接受，而当接受度小于1时，我们将相应地拒绝。因此，Metropolis-Hastings算法包含以下内容:

初始化：随机选择一个初始状态x； 。

根据q（x'| x）随机选择一个新状态x',

3.接受根据α（x'| x）的状态。如果不接受，则不会进行转移，因此无需更新任何内容。否则，转移为x'； 。

4.转移到2，直到生成T状态； 。

5.保存状态x，执行2.

原则上，我们从分布P（x）提取保存的状态，因为步骤4保证它们是不相关的。必须根据候选分布等不同因素来选择T的值。 重要的是，尚不清楚应该使用哪种分布q（x'| x）；必须针对当前的特定问题进行调整.

---

  。

属性

Metropolis-Hastings算法的一个有趣特性是它仅取决于比率 。

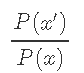
是候选样本x'与先前样本xt之间的概率， 。

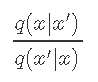
是两个方向（从xt到x'，反之亦然）的候选密度之比。如果候选密度对称，则等于1.

马尔可夫链从任意初始值x0开始，并且算法运行多次迭代，直到“初始状态”被“忘记”为止。这些被丢弃的样本称为预烧（burn-in）。其余的x可接受值集代表分布P（x）中的样本 。

---

  。

Metropolis采样

一个简单的Metropolis-Hastings采样 。

让我们看看从伽玛分布模拟任意形状和比例参数，使用具有Metropolis-Hastings采样算法.

下面给出了Metropolis-Hastings采样器的函数。该链初始化为零，并在每个阶段都建议使用N（a / b，a /（b * b））个候选对象.

基于正态分布且均值和方差相同gamma的Metropolis-Hastings独立采样 。

从某种状态开始xt。代码中的x。在代码中提出一个新的状态x'候选计算“接受概率” 。

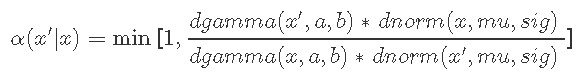
从[0,1] 得出一些均匀分布的随机数u；如果u <α接受该点，则设置xt + 1 = x'。否则，拒绝它并设置xt + 1 = xt.

  。

MH可视化

set.seed(123)  for (i in 2:n) {      can <- rnorm(1, mu, sig)      aprob <- min(1, (dgamma(can, a, b)/dgamma(x,           a, b))/(dnorm(can, mu, sig)/dnorm(x,           mu, sig)))      u <- runif(1)      if (u < aprob)           x <- can      vec[i] <- x

  。

画图

设置参数.

nrep<- 54000burnin<- 4000shape<- 2.5rate<-2.6

修改图，仅包含预烧期后的链 。

vec=vec[-(1:burnin)]#vec=vec[burnin:length(vec)]

par(mfrow=c(2,1)) # 更改主框架，在一帧中有多少个图形plot(ts(vec), xlab="Chain", ylab="Draws")abline(h = mean(vec), lwd="2", col="red" )

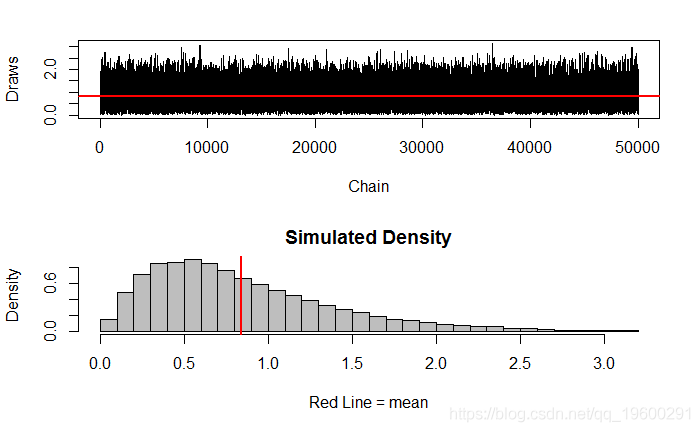
Min. 1st Qu.  Median   Mean 3rd Qu.   Max. 0.007013 0.435600 0.724800 0.843300 1.133000 3.149000

var(vec[-(1:burnin)])

[1] 0.2976507

  。

初始值

第一个样本vec是我们链的初始/起始值。我们可以更改它，以查看收敛是否发生了变化.

x <- 3*a/b  vec[1] <- x

  。

选择方案

如果候选密度与目标分布P（x）的形状匹配，即q（x'| xt）≈P（x'）q（x'|），则该算法效果最佳。 xt）≈P（x'）。如果使用正态候选密度q，则在预烧期间必须调整方差参数σ2.

通常，这是通过计算接受率来完成的，接受率是在最后N个样本的窗口中接受的候选样本的比例.

如果σ2太大，则接受率将非常低，因为候选可能落在概率密度低得多的区域中，因此a1将非常小，且链将收敛得非常慢.

---

示例2：回归的贝叶斯估计 。

Metropolis-Hastings采样用于贝叶斯估计回归模型.

---

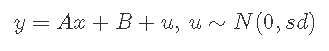
设定参数 。

---

DGP和图 。

# 创建独立的x值，大约为零x <- (-(Size-1)/2):((Size-1)/2)# 根据ax + b + N（0，sd）创建相关值y <- trueA * x + trueB + rnorm(n=Size,mean=0,sd=trueSd)

---

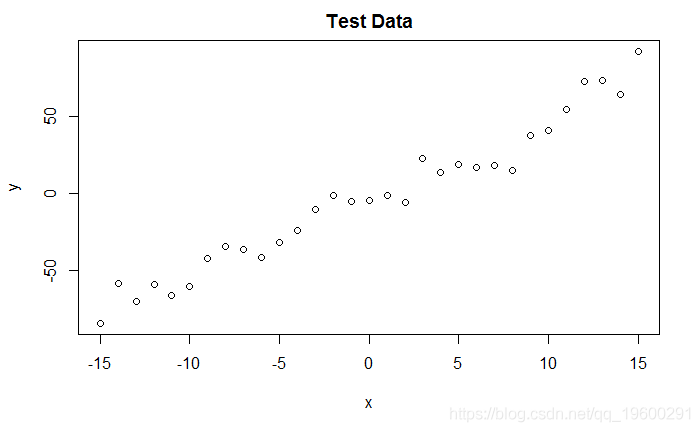
正态分布拟然 。

pred = a*x + bsinglelikelihoods = dnorm(y, mean = pred, sd = sd, log = T)sumll = sum(singlelikelihoods)

---

为什么使用对数 。

似然函数中概率的对数，这也是我求和所有数据点的概率（乘积的对数等于对数之和）的原因.

我们为什么要做这个？强烈建议这样做，因为许多小概率相乘的概率会变得很小。在某个阶段，计算机程序会陷入数值四舍五入或下溢问题.

因此，当您编写概率时，请始终使用对数 。

---

示例：绘制斜率a的似然曲线 。

# 示例：绘制斜率a的似然曲线plot (seq(3, 7, by=.05), slopelikelihoods , type="l")

---

  。

先验分布

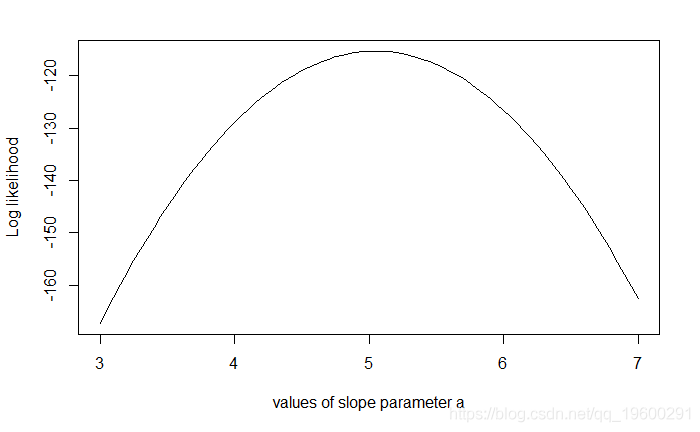
这三个参数的均匀分布和正态分布.

# 先验分布# 更改优先级，log为True，因此这些均为logdensity/likelihoodaprior = dunif(a, min=0, max=10, log = T)bprior = dnorm(b, sd = 2, log = T)sdprior = dunif(sd, min=0, max=30, log = T)

---

  。

后验

先验和概率的乘积是MCMC将要处理的实际量。此函数称为后验函数。同样，这里我们使用和，因为我们使用对数.

posterior <- function(param){return (likelihood(param) + prior(param))}

---

  。

Metropolis算法

该算法是从后验密度中采样最常见的贝叶斯统计应用之一.

1. 上面定义的后验。
2. 从随机参数值开始
3. 根据某个候选函数的概率密度，选择一个接近旧值的新参数值
4. 以概率p（new）/ p（old）跳到这个新点，其中p是目标函数，并且p> 1也意味着跳跃
5. 请注意，我们有一个对称的跳跃/候选分布q（x'| x）。

标准差σ是固定的.

所以接受概率等于 。

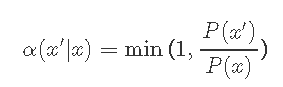
######## Metropolis 算法 ################for (i in 1:iterations){     probab = exp(posterior(proposal) - posterior(chain[i,]))  if (runif(1) < probab){    chain[i+1,] = proposal  }else{    chain[i+1,] = chain[i,]  }

  。

实施

（e）输出接受的值，并解释.

chain = metrMCMC(startvalue, 5500)burnIn = 5000accep = 1-mean(duplicated(chain[-(1:burnIn),]))

算法的第一步可能会因初始值而有偏差，因此通常会被丢弃来进行进一步分析（预烧期）。令人感兴趣的输出是接受率：候选多久被算法接受拒绝一次？候选函数会影响接受率：通常，候选越接近，接受率就越大。但是，非常高的接受率通常是无益的：这意味着算法在同一点上“停留”，这导致对参数空间（混合）的处理不够理想.

我们还可以更改初始值，以查看其是否更改结果/是否收敛.

startvalue = c(4,0,10)

---

  。

小结

V1       V2        V3    Min.  :4.068  Min.  :-6.7072  Min.  : 6.787 1st Qu.:4.913  1st Qu.:-2.6973  1st Qu.: 9.323 Median :5.052  Median :-1.7551  Median :10.178 Mean  :5.052  Mean  :-1.7377  Mean  :10.385 3rd Qu.:5.193  3rd Qu.:-0.8134  3rd Qu.:11.166 Max.  :5.989  Max.  : 4.8425  Max.  :19.223

#比较:summary(lm(y~x))

Call:lm(formula = y ~ x)Residuals:Min   1Q Median   3Q   Max -22.259 -6.032 -1.718  6.955 19.892 Coefficients:    Estimate Std. Error t value Pr(>|t|)  (Intercept) -3.1756   1.7566 -1.808  0.081 . x       5.0469   0.1964 25.697  <2e-16 ***---Signif. codes: 0 ?**?0.001 ?*?0.01 ??0.05 ??0.1 ??1Residual standard error: 9.78 on 29 degrees of freedomMultiple R-squared: 0.9579,  Adjusted R-squared: 0.9565 F-statistic: 660.4 on 1 and 29 DF, p-value: < 2.2e-16

summary(lm(y~x))$sigma

[1] 9.780494

coefficients(lm(y~x))[1]

(Intercept) -3.175555

coefficients(lm(y~x))[2]

 x 5.046873

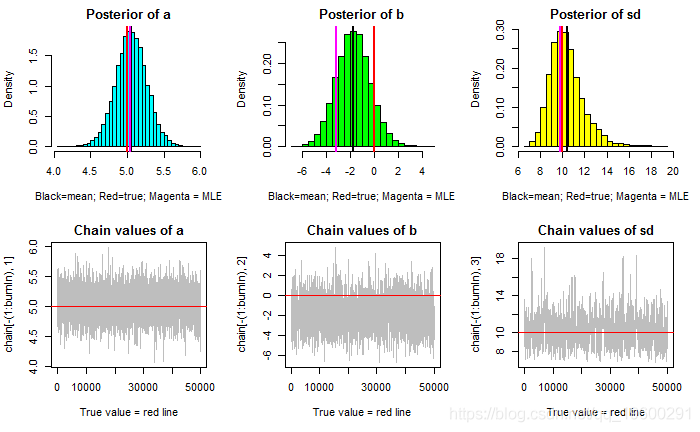
总结:

### 总结: #######################par(mfrow = c(2,3))hist(chain[-(1:burnIn),1],prob=TRUE,nclass=30,col="109" abline(v = mean(chain[-(1:burnIn),1]), lwd="2")

---

到此这篇关于R语言MCMC:Metropolis-Hastings采样用于回归的贝叶斯估计的文章就介绍到这了,更多相关R语言MCMC:Metropolis-Hastings采样用于回归的贝叶斯估计内容请搜索我以前的文章或继续浏览下面的相关文章希望大家以后多多支持我！ 。

原文链接：https://blog.csdn.net/qq_19600291/article/details/106119236 。

最后此篇关于详解R语言MCMC:Metropolis-Hastings采样用于回归的贝叶斯估计的文章就讲到这里了,如果你想了解更多关于详解R语言MCMC:Metropolis-Hastings采样用于回归的贝叶斯估计的内容请搜索CFSDN的文章或继续浏览相关文章，希望大家以后支持我的博客！ 。