CFSDN坚持开源创造价值，我们致力于搭建一个资源共享平台，让每一个IT人在这里找到属于你的精彩世界.

这篇CFSDN的博客文章R语言编程数学分析重读微积分理解极限算法由作者收集整理，如果你对这篇文章有兴趣，记得点赞哟.

1 状态变化

若将数学整体划分为三类，则可概括为代数、几何与分析。对于前两者，我们很早就建立了直观的概念，对于空间结构及其性质的研究，即为几何；以数为核心的研究领域，即为代数.

而分析则具备更多的非数学的内涵，所以初学者往往难以看透数学分析所指向的数学本质，如果望文生义，会更倾向于将“分析”理解为一门数学技巧，而非数学领域.

我们最先接触数学分析时，是将其等同为微积分的。可以认为微积分是数学分析最基本的知识对象，而微积分的理论基础建立在极限之上。所以，我们可以将极限作为分析学的根基，为此，需要去理解极限的本质，而极限本身则是一个动态的过程，例如下面这个重要极限 。

画图方法有很多，在此使用R语言，在RStudio中画出，之所以用RStudio，是因为其界面对初学者来说更友好。输入 。

> x = c(1:100)				#定义x为1到100的数组> y = x*sin(1/x)> plot(x,y,type='l',xlab='x',ylab='y=x・sin(1/x)')	#画图

得到 。

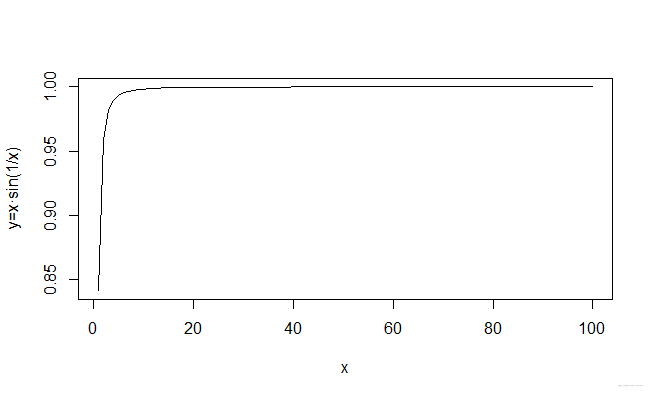
可以非常清晰地看到，当x逐渐变大的时候，y是趋于1的。这个趋势可以让我们更加容易理解：极限是一种动态过程；同时有助于形成对分析学的更加直观的印象――分析是建立在状态变化上的一种动态的数学.

一旦建立了这种动态的思维，就会发现原本安定本分的数学世界也发生了微妙的变化，例如，我们又将如何理解1这个整数.

例如无限循环小数0.999...=1这个反直觉的等式是否严格。在初等的观点看来，可以很容易得到 10 × 0.999... = 9.999... → ( 10 − 1 ) ∗ 0.999... = 9 → 0.999... = 1 .

进而敏锐地发现，若用一种不厌其烦的方式去求解分式1 \1，会更加自然地得到0.999... 。

但无论如何，0.999...=1是反直觉的，反来自于初等数学的直觉。换句话说，初等数学的直觉存在矛盾，我们需要一个更加严格的有关极限的定义和表示，尤其需要建立一种可以称之为相等的映射关系.

  。

2 极限语言

初学数学分析的时候，很多人包括我在内，都对 ε − N深恶痛绝，更妙的是，不理解这种表达方式，对做题似乎影响不大。大部分人通过加深对上面的那三个约定（以及更多约定）的记忆来完成解题，从而避免了加深对数学对象的理解.

其实这个语句并不难理解，当我们最开始接触无穷大这个概念的时候，是在描述自然数的个数。那时我们常说的可能是，无论你举出一个多么大的自然数，我都能举出一个更大的数，所以自然数是无穷的.

> x = c(10:100)> y = 1-x*sin(1/x)> > plot(x,y,type='l',xlab='x',ylab='y=1-x・sin(1/x)')

其图像为 。

  。

3 序列与函数

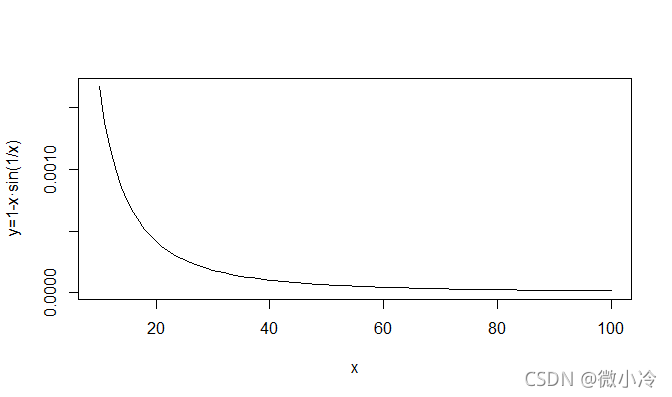
若从映射的角度去考察序列与函数，则二者最大的区别是定义域。序列是定义域为正整数的特殊函数。相比之下，微积分中大多名之为函数的映射，都定义在实数域上。从而在函数的定义域中，随便抽选出一个区间，其元素个数都是无穷多的。即对于区间 [ a , b ]而言，只要 a ≠ b ，则区间中的元素个数就是无穷多个.

好在我们有了极限的概念，极限在 ε − N意义上重新定义了相等，从而意味着每一个实数都包含了无穷多种初等的表示，即 1 = 0.999...0 = 0.999...1 = 0.999... n , n 1=0.999...0=0.999...1=0.999...n,n为任意长度的数串，中间的无穷多位，导致末位信息在变得毫无意义，乃至于根本不存在最后一位.

这时我们会异想天开地希望建立整数与实数的对应关系，例如将整数环映射到区间 [ − 1 , 1 ] 内，这个区间也会出现实数区间的性质，即任意一个长度大于一的子区间，存在无穷多个元素。但众所周知，实数的个数是比整数更高的无穷，也就是说实数区间 [ − 1 , 1 ] 的元素个数是远多于整数的.

当然，我们此后会接触更多的让人摸不着头脑的函数，这些函数过于奇葩，以至于上面的这些似乎完全不适用呢。。.

  。

4 极限常数

圆周率 π

历史上很早就产生了极限思想，而割圆术就是这种思想的绝佳体现.

N = c(3:100)Pi = N*sin(pi/N)plot(N,Pi,type='l',xlab='N',ylab='Pi')

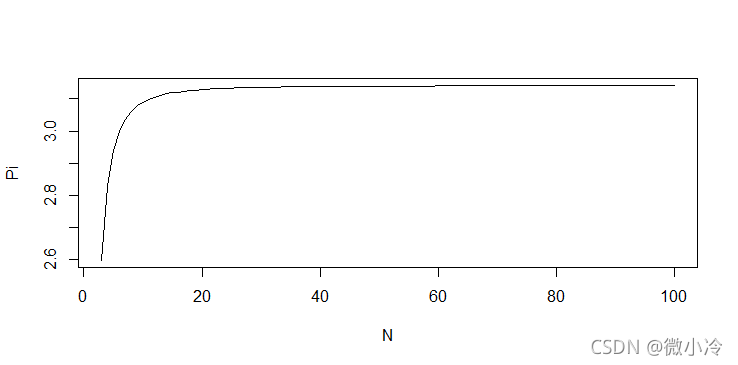
由于到了后面，误差变得越来越小，所以用对数来看一下误差的变化 。

N = c(3:10000)err =log(pi-N*sin(pi/N),10)plot(N,err,type='l',xlab='N',ylab='err')

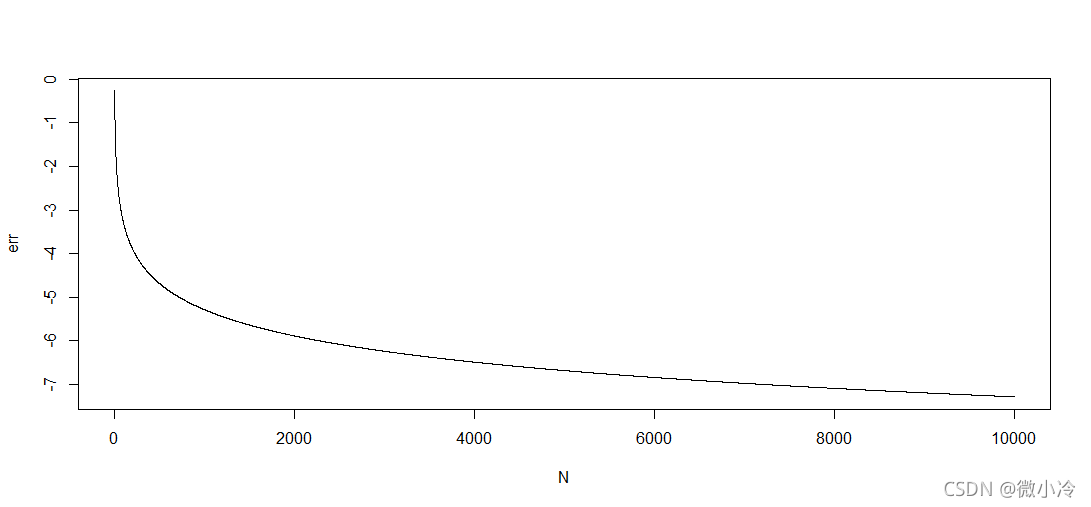
可见割到了正10000边形，也只能得到 1 0 − 7 10^{-7} 10−7的精度，通过计算可以得到正10000边形算出的圆周率约为3.14159260，所以我们至今也无法知道祖冲之他老人家到底是怎么得到的.

options(digits=15)10000*sin(pi/10000)[1] 3.14159260191267

圆周率的这种定义其实也提供了一个重要极限，即 。

自然对数e

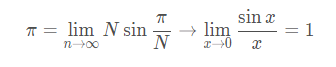
很多人喜欢把自然对数和复利计算联系在一起.

问题来了，是不是随着 n n n逐渐增大，一年的收获会越来越多呢?

为了计算方便，假设 x = 1 ，即正常 W 存一年，一年之后本息翻倍为2W.

结果发现 。

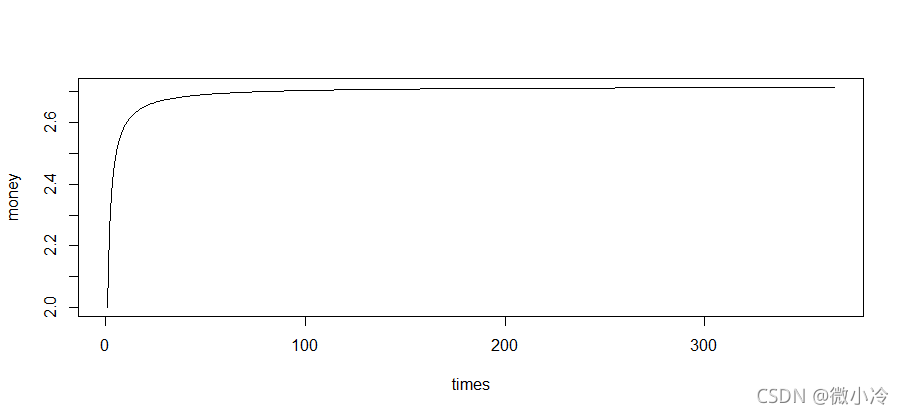
最终这个值趋近于一个常数，这个常数就定义为 e，看来一年最多翻e倍，这个方法没办法发财了。但至少明白了一个著名的极限 。

很合理.

欧拉常数 γ

对 e两侧以 e为底取对数，可得 。

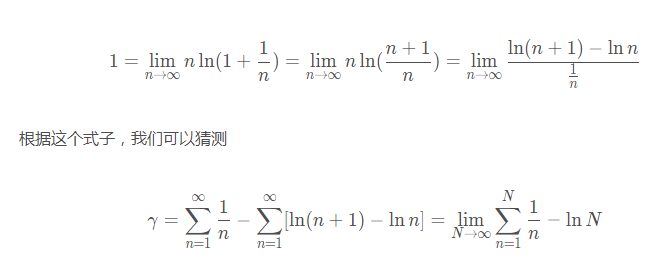
是一个常数:

N = c(1:10000)for(i in c(1:0000)){  H[i]=sum(1/N[0:i])}plot(N,gamma,type='l',xlab='N',ylab='gamma')gamma[10000][1] 0.577265664068198

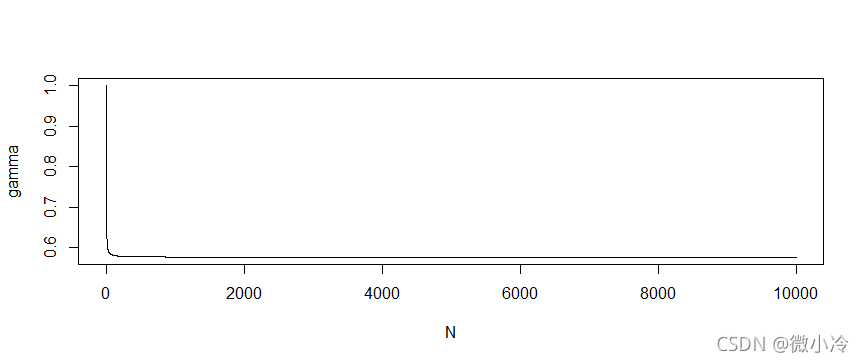
我们猜对了，这个常数即欧拉常数.

其证明过程也不复杂 。

  。

5 洛必达法则

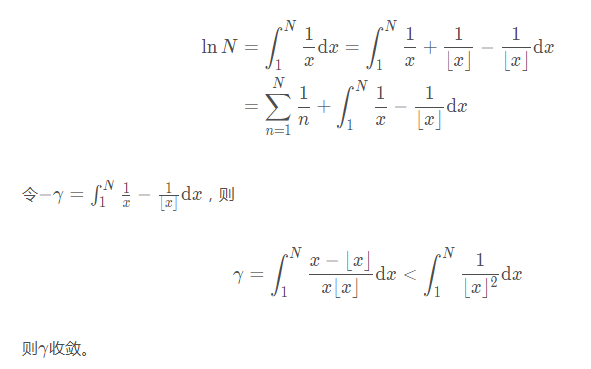
令 N 为常数，则常规的极限运算大致有以下几种 。

所以，尽管二者都为0，但0和0也有不同。问题是这种不同是否明显？如果定义域在 [ − 1 , 1 ] 这个区间，的确看不出太多的区别 。

x = seq(-1,1,0.01)  #生成等差数列plot(x,x^2,type='l')lines(x,x^3)lines(x,x^4)lines(x,x^5)lines(x,x^6)

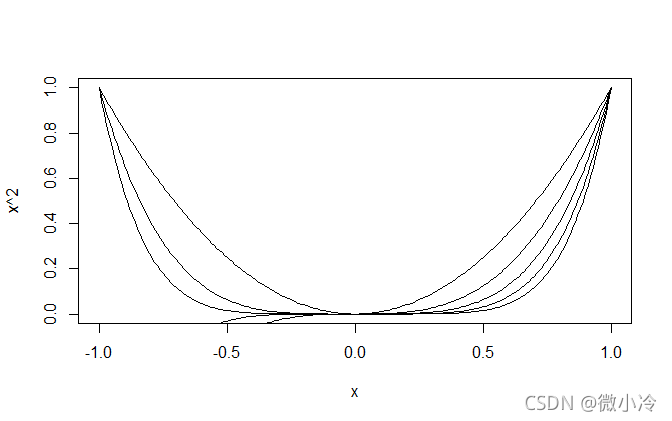
然而随着坐标尺度的缩小，区别变得明显起来 。

> x = seq(-0.1,0.1,0.001)> plot(x,x^2,type='l')> lines(x,x^3)

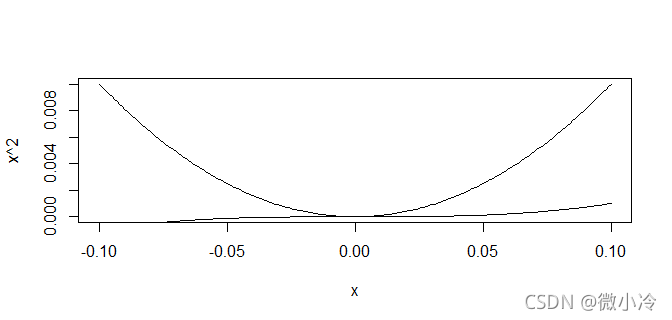
这意味着越是逼近0，不同阶数的幂函数将渐行渐远，回顾极限的定义，对于 。

受到这种运算形式的启发，对于一个相对复杂的表达式，或许可以对上式进行一点更改 。

可以画图验证一下二者在趋近于0时的特性 。

x = seq(-0.01,0.01,0.001)plot(x,x,ylab="x/sin(x)")lines(x,sin(x),col='red')

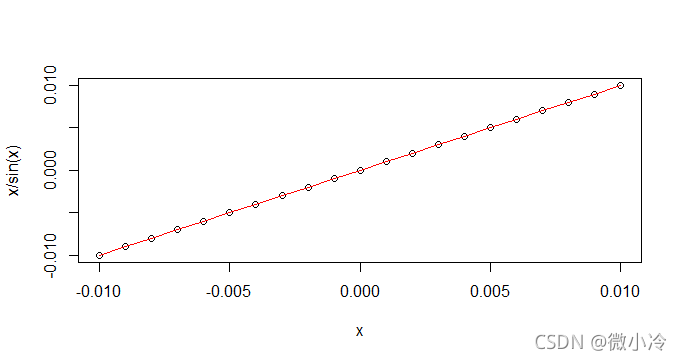
由于实在靠的太近，所以用差的对数来表示一下 。

x = seq(-0.1,0.1,0.001)err = log(abs(x-sin(x)),10)plot(x,err,type='l')

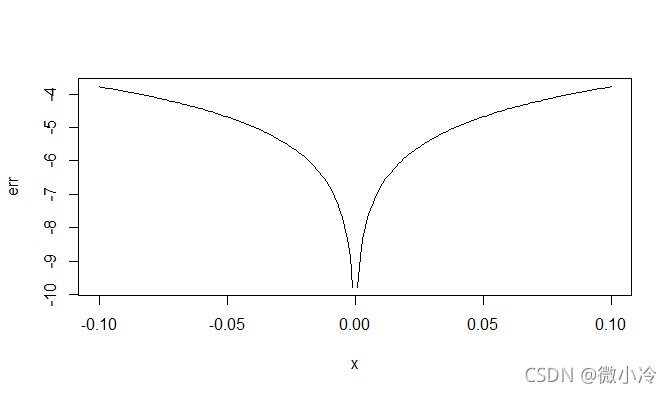
可见这个收敛速度是很快的，当 x = 0.001时，二者之间的差就已经达到了 10^ -9 。

以上就是R语言编程重读微积分数学分析理解极限算法 的详细内容，更多关于R语言编微积分数学分析极限算法 的资料请关注我其它相关文章！ 。

原文链接：https://blog.csdn.net/m0_37816922/article/details/120551847 。

最后此篇关于R语言编程数学分析重读微积分理解极限算法的文章就讲到这里了,如果你想了解更多关于R语言编程数学分析重读微积分理解极限算法的内容请搜索CFSDN的文章或继续浏览相关文章，希望大家以后支持我的博客！ 。