- ubuntu12.04环境下使用kvm ioctl接口实现最简单的虚拟机
- Ubuntu 通过无线网络安装Ubuntu Server启动系统后连接无线网络的方法
- 在Ubuntu上搭建网桥的方法
- ubuntu 虚拟机上网方式及相关配置详解
CFSDN坚持开源创造价值,我们致力于搭建一个资源共享平台,让每一个IT人在这里找到属于你的精彩世界.
这篇CFSDN的博客文章回归预测分析python数据化运营线性回归总结由作者收集整理,如果你对这篇文章有兴趣,记得点赞哟.
以 python 使用 线性回归 简单举例应用介绍回归分析.
线性回归是利用线性的方法,模拟因变量与一个或多个自变量之间的关系; 。
对于模型而言,自变量是输入值,因变量是模型基于自变量的输出值,适用于x和y满足线性关系的数据类型的应用场景.
用于预测输入变量和输出变量之间的关系,特别是当输入变量的值发生变化时,输出变量的值也随之发生变化.
回归模型正是表示从输入变量到输出变量之间映射的函数.
线性回归几乎是最简单的模型了,它假设因变量和自变量之间是线性关系的,一条直线简单明了.
连续性数据的预测:例如房价预测、销售额度预测、贷款额度预测.
简单来说就是用历史的连续数据去预测未来的某个数值.
最小二乘法、贝叶斯岭回归、弹性网络回归、支持向量机回归、支持向量机回归等.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
import
numpy as np
# numpy库
from
sklearn.linear_model
import
bayesianridge, linearregression, elasticnet,lasso
# 批量导入要实现的回归算法
from
sklearn.svm
import
svr
# svm中的回归算法
from
sklearn.ensemble.gradient_boosting
import
gradientboostingregressor
# 集成算法
from
sklearn.model_selection
import
cross_val_score
# 交叉检验
from
sklearn.metrics
import
explained_variance_score, mean_absolute_error, mean_squared_error, r2_score
# 批量导入指标算法
import
pandas as pd
# 导入pandas
import
matplotlib.pyplot as plt
# 导入图形展示库
import
random
# 随机生成100组包含5组特征的数据
feature
=
[[random.random(),random.random(),random.random(),random.random(),random.random()]
for
i
in
range
(
100
)]
dependent
=
[
round
(random.uniform(
1
,
100
),
2
)
for
i
in
range
(
100
)]
# 训练回归模型
n_folds
=
6
# 设置交叉检验的次数
model_br
=
bayesianridge()
# 建立贝叶斯岭回归模型对象
model_lr
=
linearregression()
# 建立普通线性回归模型对象
model_etc
=
elasticnet()
# 建立弹性网络回归模型对象
model_svr
=
svr()
# 建立支持向量机回归模型对象
model_la
=
lasso()
# 建立支持向量机回归模型对象
model_gbr
=
gradientboostingregressor()
# 建立梯度增强回归模型对象
model_names
=
[
'bayesianridge'
,
'linearregression'
,
'elasticnet'
,
'svr'
,
'lasso'
,
'gbr'
]
# 不同模型的名称列表
model_dic
=
[model_br, model_lr, model_etc, model_svr,model_la, model_gbr]
# 不同回归模型对象的集合
cv_score_list
=
[]
# 交叉检验结果列表
pre_y_list
=
[]
# 各个回归模型预测的y值列表
for
model
in
model_dic:
# 读出每个回归模型对象
scores
=
cross_val_score(model, feature, dependent, cv
=
n_folds)
# 将每个回归模型导入交叉检验模型中做训练检验
cv_score_list.append(scores)
# 将交叉检验结果存入结果列表
pre_y_list.append(model.fit(feature, dependent).predict(feature))
# 将回归训练中得到的预测y存入列表
|
model_gbr:拟合贝叶斯岭模型,以及正则化参数lambda(权重的精度)和alpha(噪声的精度)的优化.
model_lr:线性回归拟合系数w=(w1,…)的线性模型,wp)将观测到的目标与线性近似预测的目标之间的残差平方和降到最小.
model_etc:以l1和l2先验组合为正则元的线性回归.
model_svr:线性支持向量回归.
model_la:用l1先验作为正则化器(又称lasso)训练的线性模型 。
|
1
2
3
4
5
6
7
8
9
10
11
|
# 模型效果指标评估
model_metrics_name
=
[explained_variance_score, mean_absolute_error, mean_squared_error, r2_score]
# 回归评估指标对象集
model_metrics_list
=
[]
# 回归评估指标列表
for
i
in
range
(
6
):
# 循环每个模型索引
tmp_list
=
[]
# 每个内循环的临时结果列表
for
m
in
model_metrics_name:
# 循环每个指标对象
tmp_score
=
m(dependent, pre_y_list[i])
# 计算每个回归指标结果
tmp_list.append(tmp_score)
# 将结果存入每个内循环的临时结果列表
model_metrics_list.append(tmp_list)
# 将结果存入回归评估指标列表
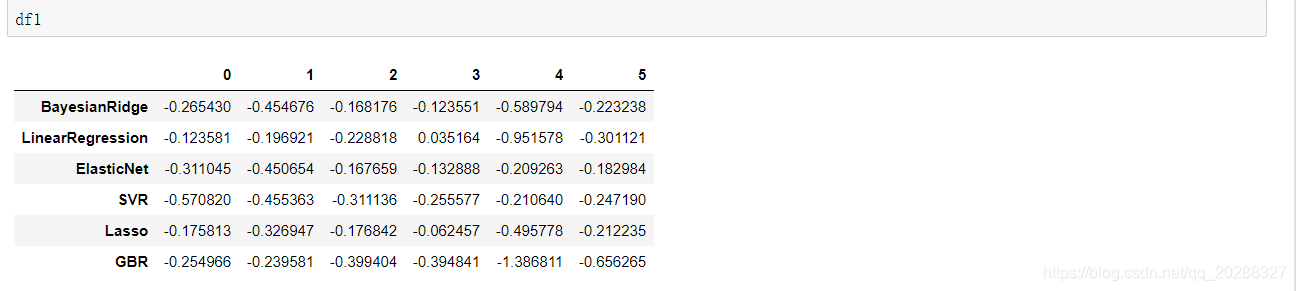
df1
=
pd.dataframe(cv_score_list, index
=
model_names)
# 建立交叉检验的数据框
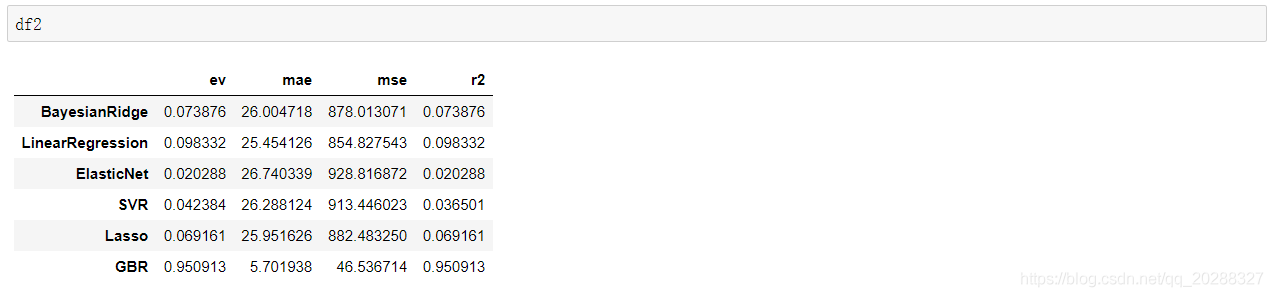
df2
=
pd.dataframe(model_metrics_list, index
=
model_names, columns
=
[
'ev'
,
'mae'
,
'mse'
,
'r2'
])
# 建立回归指标的数据框
|
|
1
2
3
4
5
6
7
8
9
10
11
|
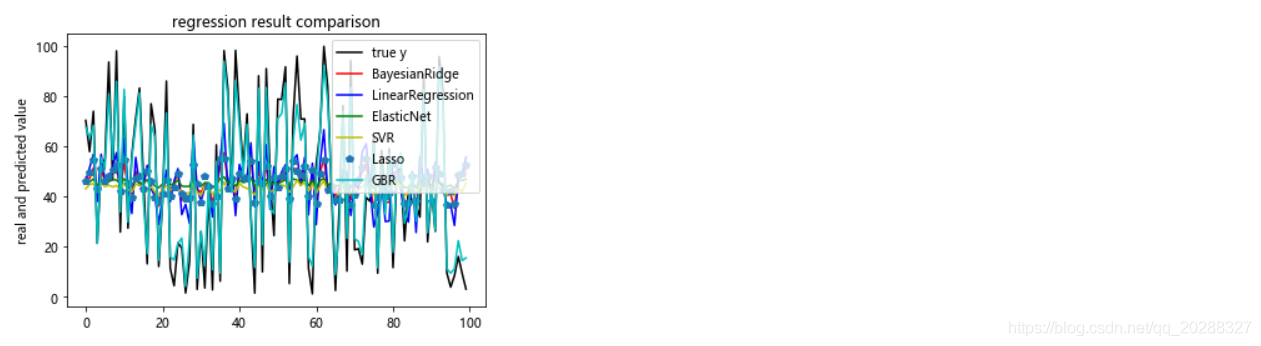
# 模型效果可视化
plt.figure()
# 创建画布
plt.plot(np.arange(
len
(feature)), dependent, color
=
'k'
, label
=
'true y'
)
# 画出原始值的曲线
color_list
=
[
'r'
,
'b'
,
'g'
,
'y'
,
'p'
,
'c'
]
# 颜色列表
linestyle_list
=
[
'-'
,
'.'
,
'o'
,
'v'
,
':'
,
'*'
]
# 样式列表
for
i, pre_y
in
enumerate
(pre_y_list):
# 读出通过回归模型预测得到的索引及结果
plt.plot(np.arange(
len
(feature)), pre_y_list[i], color_list[i], label
=
model_names[i])
# 画出每条预测结果线
plt.title(
'regression result comparison'
)
# 标题
plt.legend(loc
=
'upper right'
)
# 图例位置
plt.ylabel(
'real and predicted value'
)
# y轴标题
plt.show()
# 展示图像
|
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
|
# 模型应用
new_point_set
=
[[random.random(),random.random(),random.random(),random.random(),random.random()],
[random.random(),random.random(),random.random(),random.random(),random.random()],
[random.random(),random.random(),random.random(),random.random(),random.random()],
[random.random(),random.random(),random.random(),random.random(),random.random()]]
# 要预测的新数据集
print
(
"贝叶斯岭回归模型预测结果:"
)
for
i, new_point
in
enumerate
(new_point_set):
# 循环读出每个要预测的数据点
new_pre_y
=
model_gbr.predict(np.array(new_point).reshape(
1
,
-
1
))
print
(
'预测随机数值 %d 是: %.2f'
%
(i
+
1
, new_pre_y))
# 打印输出每个数据点的预测信息
print
(
50
*
'-'
)
print
(
"普通线性回归模型预测结果:"
)
for
i, new_point
in
enumerate
(new_point_set):
# 循环读出每个要预测的数据点
new_pre_y
=
model_lr.predict(np.array(new_point).reshape(
1
,
-
1
))
print
(
'预测随机数值 %d 是: %.2f'
%
(i
+
1
, new_pre_y))
# 打印输出每个数据点的预测信息
print
(
50
*
'-'
)
print
(
"弹性网络回归模型预测结果:"
)
for
i, new_point
in
enumerate
(new_point_set):
# 循环读出每个要预测的数据点
new_pre_y
=
model_etc.predict(np.array(new_point).reshape(
1
,
-
1
))
print
(
'预测随机数值 %d 是: %.2f'
%
(i
+
1
, new_pre_y))
# 打印输出每个数据点的预测信息
print
(
50
*
'-'
)
print
(
"支持向量机回归模型预测结果:"
)
for
i, new_point
in
enumerate
(new_point_set):
# 循环读出每个要预测的数据点
new_pre_y
=
model_svr.predict(np.array(new_point).reshape(
1
,
-
1
))
print
(
'预测随机数值 %d 是: %.2f'
%
(i
+
1
, new_pre_y))
# 打印输出每个数据点的预测信息
print
(
50
*
'-'
)
print
(
"拉索回归模型预测结果:"
)
for
i, new_point
in
enumerate
(new_point_set):
# 循环读出每个要预测的数据点
new_pre_y
=
model_la.predict(np.array(new_point).reshape(
1
,
-
1
))
print
(
'预测随机数值 %d 是: %.2f'
%
(i
+
1
, new_pre_y))
# 打印输出每个数据点的预测信息
|

以上就是回归预测分析python数据化运营线性回归总结的详细内容,更多关于python数据化运营线性回归的资料请关注我其它相关文章! 。
原文链接:https://blog.csdn.net/qq_20288327/article/details/119862345 。
最后此篇关于回归预测分析python数据化运营线性回归总结的文章就讲到这里了,如果你想了解更多关于回归预测分析python数据化运营线性回归总结的内容请搜索CFSDN的文章或继续浏览相关文章,希望大家以后支持我的博客! 。
SpruceMail 是一款 SaaS 产品,可帮助公司发布赚钱的 Facebook 广告。产品的价值定位很简单:Facebook 广告是复杂的。你要折腾很多事情,可能很快几千美元就花掉了却回报
别人的成功经验抄不来,但是别人遇到的坑我们可以躲。能够躲过越多的坑离目标就越近。 别人的成功经验抄不来,但是别人遇到的坑我们可以躲。能够躲过越多的坑离目标就越近。本人虽然进入互联网行业

我是一名优秀的程序员,十分优秀!