- ubuntu12.04环境下使用kvm ioctl接口实现最简单的虚拟机
- Ubuntu 通过无线网络安装Ubuntu Server启动系统后连接无线网络的方法
- 在Ubuntu上搭建网桥的方法
- ubuntu 虚拟机上网方式及相关配置详解
CFSDN坚持开源创造价值,我们致力于搭建一个资源共享平台,让每一个IT人在这里找到属于你的精彩世界.
这篇CFSDN的博客文章java 排序算法之冒泡排序由作者收集整理,如果你对这篇文章有兴趣,记得点赞哟.
。
冒泡排序(Bubble Sorting)(时间复杂度为 O(n²))的基本思想:通过对待排序序列 从前向后(从下标较小的元素开始),依次比较相邻元素的值,若发现逆序则交换,使值较大的元素逐渐从前移向后部,就像水底下的旗袍一样逐渐向上冒.
优化点:因为排序过程中,个元素不断接近自己的位置,如果一趟比较下来没有进行过交换,就说明序列有序,因此要在排序过程中设置一个标志判断元素是否进行过交换。从而减少不必要的比较。(该优化点可以在完成基本的冒泡排序之后再做) 。
。
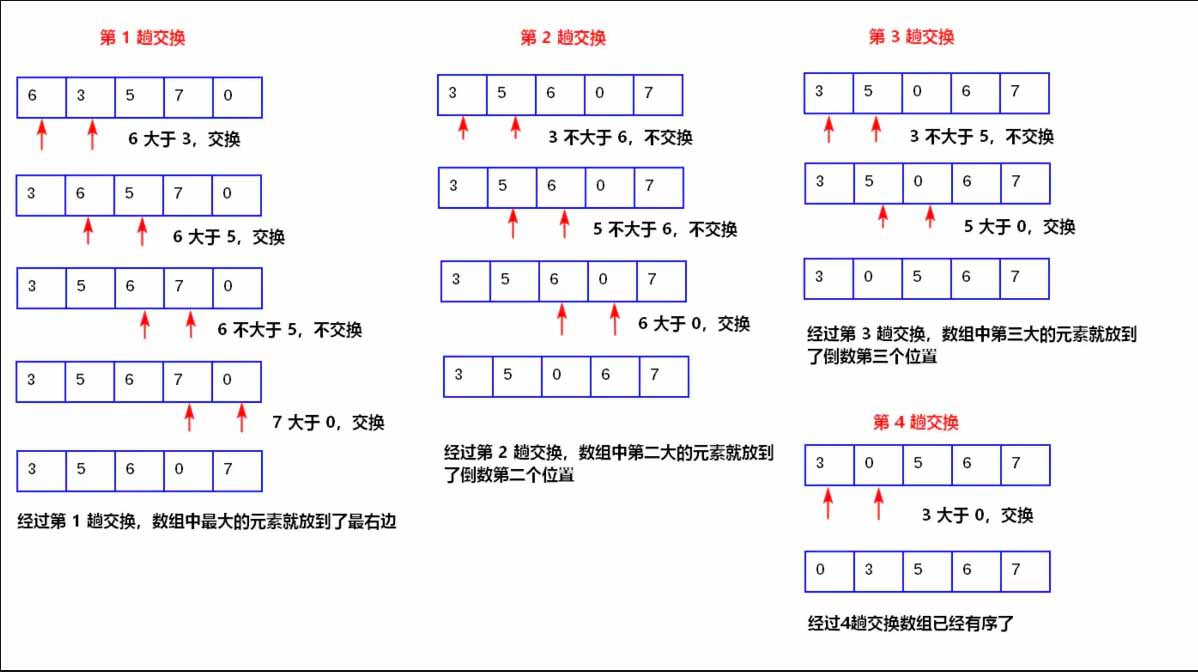
动图:
冒泡排序小结:
1.共进行 数组大小 - 1 次大的循环 。
2.每一趟排序的次数在逐渐的减少 。
3.优化:如果发现在某趟排序中,没有发生一次交换,则可以提前结束冒泡排序.
。
。
为了容易理解,先演示冒泡排序的演变过程 。
/** * 为了更好的理解,这里把冒泡排序的演变过程演示出来 */ @Test public void processDemo() { int arr[] = {3, 9, -1, 10, -2}; // 第 1 趟排序:将最大的数排在最后 // 总共排序:arr.length - 1 int temp = 0; // 临时变量,交换的时候使用 for (int i = 0; i < arr.length - 1; i++) { if (arr[i] > arr[i + 1]) { temp = arr[i]; arr[i] = arr[i + 1]; arr[i + 1] = temp; } } System.out.println("第 1 趟排序后的数组"); System.out.println(Arrays.toString(arr)); // 第 2 趟排序:将第 2 大的数排在倒数第 2 位 // 总共排序:arr.length - 1 - 1 ; // 从头开始排序,其他没有变化,只是将排序次数减少了一次 for (int i = 0; i < arr.length - 1 -1; i++) { if (arr[i] > arr[i + 1]) { temp = arr[i]; arr[i] = arr[i + 1]; arr[i + 1] = temp; } } System.out.println("第 2 趟排序后的数组"); System.out.println(Arrays.toString(arr)); // 第 3 趟排序:将第 3 大的数排在倒数第 3 位 // 总共排序:arr.length - 1 - 2 ; // 从头开始排序,其他没有变化,只是将排序次数减少了 2 次 for (int i = 0; i < arr.length - 1 -2; i++) { if (arr[i] > arr[i + 1]) { temp = arr[i]; arr[i] = arr[i + 1]; arr[i + 1] = temp; } } System.out.println("第 3 趟排序后的数组"); System.out.println(Arrays.toString(arr)); // 第 4 趟排序:将第 4 大的数排在倒数第 4 位 // 总共排序:arr.length - 1 - 3 ; // 从头开始排序,其他没有变化,只是将排序次数减少了 3 次 for (int i = 0; i < arr.length - 1 -3; i++) { if (arr[i] > arr[i + 1]) { temp = arr[i]; arr[i] = arr[i + 1]; arr[i + 1] = temp; } } System.out.println("第 4 趟排序后的数组"); System.out.println(Arrays.toString(arr)); // 第 5 趟没有必要,因为这里有 5 个数字,确定了 4 个数字,剩下的那一个就已经出来了 }
测试输出 。
第 1 趟排序后的数组 [3, -1, 9, -2, 10] 第 2 趟排序后的数组 [-1, 3, -2, 9, 10] 第 3 趟排序后的数组 [-1, -2, 3, 9, 10] 第 4 趟排序后的数组 [-2, -1, 3, 9, 10] 。
从上述的 4 趟排序过程来看,循环体都是一样的,只是每次循环的次数在减少,那么就可以如下简化 。
@Testpublic void processDemo2() { int arr[] = {3, 9, -1, 10, -2}; // 总共排序:arr.length - 1 int temp = 0; // 临时变量,交换的时候使用 for (int j = 0; j < arr.length - 1; j++) { for (int i = 0; i < arr.length - 1 - j; i++) { if (arr[i] > arr[i + 1]) { temp = arr[i]; arr[i] = arr[i + 1]; arr[i + 1] = temp; } } System.out.println("第 " + (j + 1) + " 趟排序后的数组"); System.out.println(Arrays.toString(arr)); }}
测试输出 。
第 1 趟排序后的数组 [3, -1, 9, -2, 10] 第 2 趟排序后的数组 [-1, 3, -2, 9, 10] 第 3 趟排序后的数组 [-1, -2, 3, 9, 10] 第 4 趟排序后的数组 [-2, -1, 3, 9, 10] 。
。
对于优化,减少排序次数 。
@Test public void processDemo3() { int arr[] = {3, 9, -1, 10, 20}; // 总共排序:arr.length - 1 int temp = 0; // 临时变量,交换的时候使用 boolean change = false;// 标识变量,表示是否进行过交换 for (int j = 0; j < arr.length - 1; j++) { for (int i = 0; i < arr.length - 1 - j; i++) { if (arr[i] > arr[i + 1]) { temp = arr[i]; arr[i] = arr[i + 1]; arr[i + 1] = temp; change = true; } } if(!change){ // 如果有 1 轮下来,都没有进行排序,则可以提前退出 break; }else{ change = false; // 重置 change!!!, 进行下次判断 } System.out.println("第 " + (j + 1) + " 趟排序后的数组"); System.out.println(Arrays.toString(arr)); } }
测试输出:
第 1 趟排序后的数组 [3, -1, 9, 10, 20] 第 2 趟排序后的数组 [-1, 3, 9, 10, 20] 。
这里更改了原始数组,因为优化的点,得看你这个数组原来的排序 和 元素组成,算是一种概率问题,并不是在任何情况下都可以被优化 。
。
/** * 把排序算法封装成一个方法,方便被复用 * * @param arr */ public static void bubbleSort(int[] arr) { // 总共排序:arr.length - 1 int temp = 0; // 临时变量,交换的时候使用 boolean change = false; for (int j = 0; j < arr.length - 1; j++) { for (int i = 0; i < arr.length - 1 - j; i++) { if (arr[i] > arr[i + 1]) { temp = arr[i]; arr[i] = arr[i + 1]; arr[i + 1] = temp; change = true; } } if(!change){ // 如果有 1 轮下来,都没有进行排序,则可以提前退出 break; }else{ change = false; // 重置 change!!!, 进行下次判断 } } }
测试调用 。
/** * 测试封装后的算法 */ @Test public void bubbleSortTest() { int[] arr = {3, 9, -1, 10, 20}; System.out.println("排序前:" + Arrays.toString(arr)); bubbleSort(arr); System.out.println("排序后:" + Arrays.toString(arr)); }
测试输出 。
排序前:[3, 9, -1, 10, 20] 排序后:[-1, 3, 9, 10, 20] 。
。
排序随机生成的 8 万个数据 。
/** * 大量数据排序时间测试 */ @Test public void bulkDataSort() { int max = 80000; int[] arr = new int[max]; for (int i = 0; i < max; i++) { arr[i] = (int) (Math.random() * 80000); } Instant startTime = Instant.now(); bubbleSort(arr);// System.out.println(Arrays.toString(arr)); Instant endTime = Instant.now(); System.out.println("共耗时:" + Duration.between(startTime, endTime).toMillis() + " 毫秒"); }
测试输出 。
运行几次,差不多在 13 秒左右 共耗时:14656 毫秒 共耗时:13853 毫秒 。
到此这篇关于java 排序算法之冒泡排序的文章就介绍到这了,更多相关java 冒泡排序内容请搜索我以前的文章或继续浏览下面的相关文章希望大家以后多多支持我! 。
原文链接:https://www.cnblogs.com/ljz111/p/15203778.html 。
最后此篇关于java 排序算法之冒泡排序的文章就讲到这里了,如果你想了解更多关于java 排序算法之冒泡排序的内容请搜索CFSDN的文章或继续浏览相关文章,希望大家以后支持我的博客! 。
滑动窗口限流 滑动窗口限流是一种常用的限流算法,通过维护一个固定大小的窗口,在单位时间内允许通过的请求次数不超过设定的阈值。具体来说,滑动窗口限流算法通常包括以下几个步骤: 初始化:设置窗口
表达式求值:一个只有+,-,*,/的表达式,没有括号 一种神奇的做法:使用数组存储数字和运算符,先把优先级别高的乘法和除法计算出来,再计算加法和减法 int GetVal(string s){
【算法】前缀和 题目 先来看一道题目:(前缀和模板题) 已知一个数组A[],现在想要求出其中一些数字的和。 输入格式: 先是整数N,M,表示一共有N个数字,有M组询问 接下来有N个数,表示A[1]..
1.前序遍历 根-左-右的顺序遍历,可以使用递归 void preOrder(Node *u){ if(u==NULL)return; printf("%d ",u->val);
先看题目 物品不能分隔,必须全部取走或者留下,因此称为01背包 (只有不取和取两种状态) 看第一个样例 我们需要把4个物品装入一个容量为10的背包 我们可以简化问题,从小到大入手分析 weightva
我最近在一次采访中遇到了这个问题: 给出以下矩阵: [[ R R R R R R], [ R B B B R R], [ B R R R B B], [ R B R R R R]] 找出是否有任
我正在尝试通过 C++ 算法从我的 outlook 帐户发送一封电子邮件,该帐户已经打开并记录,但真的不知道从哪里开始(对于 outlook-c++ 集成),谷歌也没有帮我这么多。任何提示将不胜感激。
我发现自己像这样编写了一个手工制作的 while 循环: std::list foo; // In my case, map, but list is simpler auto currentPoin
我有用于检测正方形的 opencv 代码。现在我想在检测正方形后,代码运行另一个命令。 代码如下: #include "cv.h" #include "cxcore.h" #include "high
我正在尝试模拟一个 matlab 函数“imfill”来填充二进制图像(1 和 0 的二维矩阵)。 我想在矩阵中指定一个起点,并像 imfill 的 4 连接版本那样进行洪水填充。 这是否已经存在于
我正在阅读 Robert Sedgewick 的《C++ 算法》。 Basic recurrences section it was mentioned as 这种循环出现在循环输入以消除一个项目的递
我正在思考如何在我的日历中生成代表任务的数据结构(仅供我个人使用)。我有来自 DBMS 的按日期排序的任务记录,如下所示: 买牛奶(18.1.2013) 任务日期 (2013-01-15) 任务标签(
输入一个未排序的整数数组A[1..n]只有 O(d) :(d int) 计算每个元素在单次迭代中出现在列表中的次数。 map 是balanced Binary Search Tree基于确保 O(nl
我遇到了一个问题,但我仍然不知道如何解决。我想出了如何用蛮力的方式来做到这一点,但是当有成千上万的元素时它就不起作用了。 Problem: Say you are given the followin
我有一个列表列表。 L1= [[...][...][.......].......]如果我在展平列表后获取所有元素并从中提取唯一值,那么我会得到一个列表 L2。我有另一个列表 L3,它是 L2 的某个
我们得到二维矩阵数组(假设长度为 i 和宽度为 j)和整数 k我们必须找到包含这个或更大总和的最小矩形的大小F.e k=7 4 1 1 1 1 1 4 4 Anwser是2,因为4+4=8 >= 7,
我实行 3 类倒制,每周换类。顺序为早类 (m)、晚类 (n) 和下午类 (a)。我固定的订单,即它永远不会改变,即使那个星期不工作也是如此。 我创建了一个函数来获取 ISO 周数。当我给它一个日期时
假设我们有一个输入,它是一个元素列表: {a, b, c, d, e, f} 还有不同的集合,可能包含这些元素的任意组合,也可能包含不在输入列表中的其他元素: A:{e,f} B:{d,f,a} C:
我有一个子集算法,可以找到给定集合的所有子集。原始集合的问题在于它是一个不断增长的集合,如果向其中添加元素,我需要再次重新计算它的子集。 有没有一种方法可以优化子集算法,该算法可以从最后一个计算点重新
我有一个包含 100 万个符号及其预期频率的表格。 我想通过为每个符号分配一个唯一(且前缀唯一)的可变长度位串来压缩这些符号的序列,然后将它们连接在一起以表示序列。 我想分配这些位串,以使编码序列的预

我是一名优秀的程序员,十分优秀!