CFSDN坚持开源创造价值，我们致力于搭建一个资源共享平台，让每一个IT人在这里找到属于你的精彩世界.

这篇CFSDN的博客文章FP-growth算法发现频繁项集——构建FP树由作者收集整理，如果你对这篇文章有兴趣，记得点赞哟.

FP代表频繁模式（Frequent Pattern)，算法主要分为两个步骤：FP-tree构建、挖掘频繁项集.

FP树表示法

FP树通过逐个读入事务，并把事务映射到FP树中的一条路径来构造。由于不同的事务可能会有若干个相同的项，因此它们的路径可能部分重叠。路径相互重叠越多，使用FP树结构获得的压缩效果越好；如果FP树足够小，能够存放在内存中，就可以直接从这个内存中的结构提取频繁项集，而不必重复地扫描存放在硬盘上的数据.

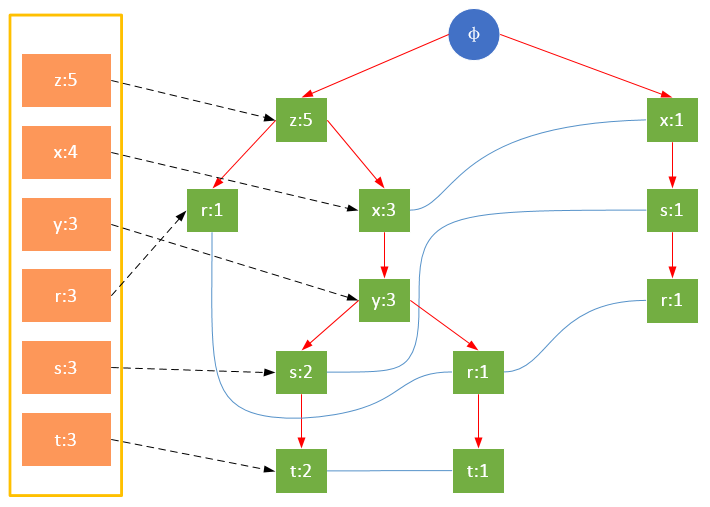
一颗FP树如下图所示:

通常，FP树的大小比未压缩的数据小，因为数据的事务常常共享一些共同项，在最好的情况下，所有的事务都具有相同的项集，FP树只包含一条节点路径；当每个事务都具有唯一项集时，导致最坏情况发生，由于事务不包含任何共同项，FP树的大小实际上与原数据的大小一样.

FP树的根节点用φ表示，其余节点包括一个数据项和该数据项在本路径上的支持度；每条路径都是一条训练数据中满足最小支持度的数据项集；FP树还将所有相同项连接成链表，上图中用蓝色连线表示.

为了快速访问树中的相同项，还需要维护一个连接具有相同项的节点的指针列表（headTable），每个列表元素包括：数据项、该项的全局最小支持度、指向FP树中该项链表的表头的指针.

构建FP树

现在有如下数据:

　　

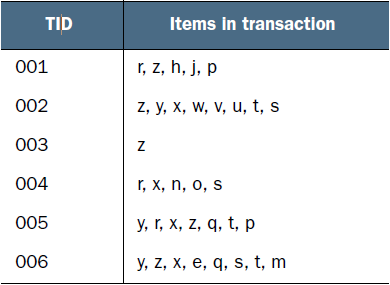
FP-growth算法需要对原始训练集扫描两遍以构建FP树.

第一次扫描，过滤掉所有不满足最小支持度的项；对于满足最小支持度的项，按照全局最小支持度排序，在此基础上，为了处理方便，也可以按照项的关键字再次排序.

第一次扫描的后的结果 。

第二次扫描，构造FP树.

参与扫描的是过滤后的数据，如果某个数据项是第一次遇到，则创建该节点，并在headTable中添加一个指向该节点的指针；否则按路径找到该项对应的节点，修改节点信息。具体过程如下所示:

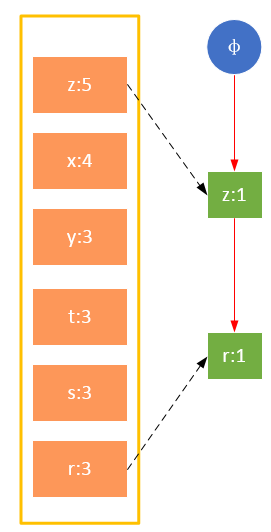
事务001，{z,x} 。

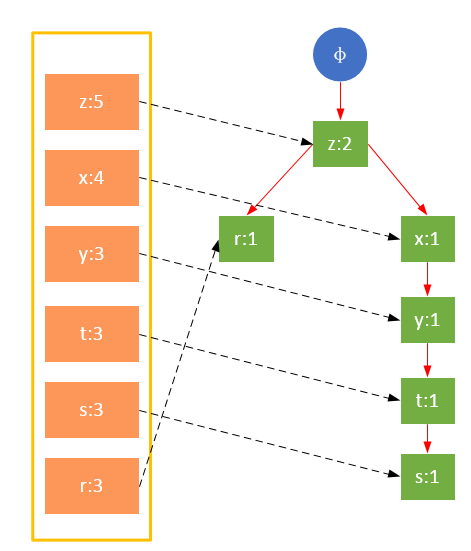
事务002，{z,x,y,t,s} 。

事务003，{z} 。

事务004，{x,s,r} 。

事务005，{z,x,y,t,r} 。

事务006，{z,x,y,t,s} 。

从上面可以看出，headTable并不是随着FPTree一起创建，而是在第一次扫描时就已经创建完毕，在创建FPTree时只需要将指针指向相应节点即可。从事务004开始，需要创建节点间的连接，使不同路径上的相同项连接成链表.

代码如下:

def loadSimpDat():    simpDat = [['r', 'z', 'h', 'j', 'p'],               ['z', 'y', 'x', 'w', 'v', 'u', 't', 's'],               ['z'],               ['r', 'x', 'n', 'o', 's'],               ['y', 'r', 'x', 'z', 'q', 't', 'p'],               ['y', 'z', 'x', 'e', 'q', 's', 't', 'm']]    return simpDatdef createInitSet(dataSet):    retDict = {}    for trans in dataSet:        fset = frozenset(trans)        retDict.setdefault(fset, 0)        retDict[fset] += 1    return retDictclass treeNode:    def __init__(self, nameValue, numOccur, parentNode):        self.name = nameValue        self.count = numOccur        self.nodeLink = None        self.parent = parentNode        self.children = {}    def inc(self, numOccur):        self.count += numOccur    def disp(self, ind=1):        print('   ' * ind, self.name, ' ', self.count)        for child in self.children.values():            child.disp(ind + 1)def createTree(dataSet, minSup=1):    headerTable = {}    #此一次遍历数据集， 记录每个数据项的支持度    for trans in dataSet:        for item in trans:            headerTable[item] = headerTable.get(item, 0) + 1    #根据最小支持度过滤    lessThanMinsup = list(filter(lambda k:headerTable[k] < minSup, headerTable.keys()))    for k in lessThanMinsup: del(headerTable[k])    freqItemSet = set(headerTable.keys())    #如果所有数据都不满足最小支持度，返回None, None    if len(freqItemSet) == 0:        return None, None    for k in headerTable:        headerTable[k] = [headerTable[k], None]    retTree = treeNode('φ', 1, None)    #第二次遍历数据集，构建fp-tree    for tranSet, count in dataSet.items():        #根据最小支持度处理一条训练样本，key:样本中的一个样例，value:该样例的的全局支持度        localD = {}        for item in tranSet:            if item in freqItemSet:                localD[item] = headerTable[item][0]        if len(localD) > 0:            #根据全局频繁项对每个事务中的数据进行排序,等价于 order by p[1] desc, p[0] desc            orderedItems = [v[0] for v in sorted(localD.items(), key=lambda p: (p[1],p[0]), reverse=True)]            updateTree(orderedItems, retTree, headerTable, count)    return retTree, headerTabledef updateTree(items, inTree, headerTable, count):    if items[0] in inTree.children:  # check if orderedItems[0] in retTree.children        inTree.children[items[0]].inc(count)  # incrament count    else:  # add items[0] to inTree.children        inTree.children[items[0]] = treeNode(items[0], count, inTree)        if headerTable[items[0]][1] == None:  # update header table            headerTable[items[0]][1] = inTree.children[items[0]]        else:            updateHeader(headerTable[items[0]][1], inTree.children[items[0]])    if len(items) > 1:  # call updateTree() with remaining ordered items        updateTree(items[1:], inTree.children[items[0]], headerTable, count)def updateHeader(nodeToTest, targetNode):  # this version does not use recursion    while (nodeToTest.nodeLink != None):  # Do not use recursion to traverse a linked list!        nodeToTest = nodeToTest.nodeLink    nodeToTest.nodeLink = targetNodesimpDat = loadSimpDat()dictDat = createInitSet(simpDat)myFPTree,myheader = createTree(dictDat, 3)myFPTree.disp()

上面的代码在第一次扫描后并没有将每条训练数据过滤后的项排序，而是将排序放在了第二次扫描时，这可以简化代码的复杂度.

控制台信息:

项的顺序对FP树的影响

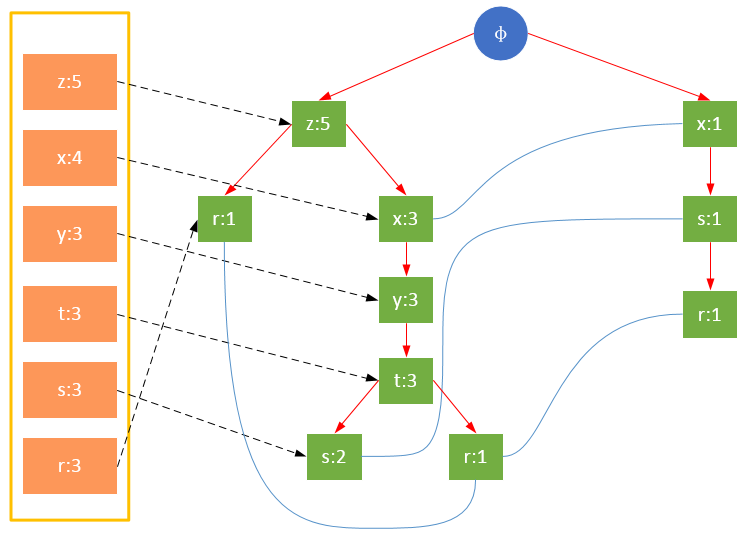
值得注意的是，对项的关键字排序将会影响FP树的结构。下面两图是相同训练集生成的FP树，图1除了按照最小支持度排序外，未对项做任何处理；图2则将项按照关键字进行了降序排序。树的结构也将影响后续发现频繁项的结果.

图1 未对项的关键字排序 。

图2 对项的关键字降序排序 。

总结　　

本篇文章就到这里了，下篇继续，介绍如何发现频繁项集。希望能给你带来帮助，也希望您能够多多关注我的更多内容！ 。

原文链接：https://www.cnblogs.com/bigmonkey/p/7478698.html 。

最后此篇关于FP-growth算法发现频繁项集——构建FP树的文章就讲到这里了,如果你想了解更多关于FP-growth算法发现频繁项集——构建FP树的内容请搜索CFSDN的文章或继续浏览相关文章，希望大家以后支持我的博客！ 。