- ubuntu12.04环境下使用kvm ioctl接口实现最简单的虚拟机
- Ubuntu 通过无线网络安装Ubuntu Server启动系统后连接无线网络的方法
- 在Ubuntu上搭建网桥的方法
- ubuntu 虚拟机上网方式及相关配置详解
CFSDN坚持开源创造价值,我们致力于搭建一个资源共享平台,让每一个IT人在这里找到属于你的精彩世界.
这篇CFSDN的博客文章python 通过可变参数计算n个数的乘积方法由作者收集整理,如果你对这篇文章有兴趣,记得点赞哟.
通过可变参数计算n个数的乘积:
代码如下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
list
=
[]
def
the_input(count
=
eval
(
input
(
"输入乘数的总个数:"
))):
for
i
in
range
(count):
n
=
eval
(
input
(
"依次输入乘数:"
))
list
.append(n)
print
(
"一共有"
,count,
"个要相乘的数"
)
print
(
"把这些乘放在列表里面:"
,
list
)
the_input()
def
get_mul(
*
num):
sum
=
1
for
n
in
num:
sum
=
sum
*
n
return
sum
print
(
"这鞋数相乘的最终结果是:"
,get_mul(
*
list
))
|
运行结果 。
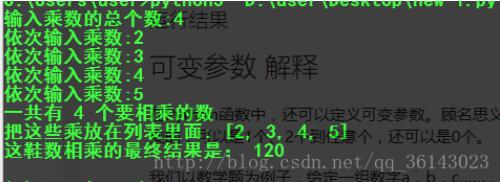
可变参数 解释 。
在python函数中,还可以定义可变参数。顾名思义,可变参数就是传入的参数个数是可变的,可以是1个、2个到任意个,还可以是0个.
我们以数学题为例子,给定一组数字a,b,c……,请计算a2 + b2 + c2 + …….
要定义出这个函数,我们必须确定输入的参数。由于参数个数不确定,我们首先想到可以把a,b,c……作为一个list或tuple传进来,这样,函数可以定义如下:
|
1
2
3
4
5
|
def
calc(numbers):
sum
=
0
for
n
in
numbers:
sum
=
sum
+
n
*
n
return
sum
|
但是调用的时候,需要先组装出一个list或tuple:
|
1
2
3
4
|
calc([
1
,
2
,
3
])
14
calc((
1
,
3
,
5
,
7
))
84
|
如果利用可变参数,调用函数的方式可以简化成这样:
|
1
2
3
4
|
calc(
1
,
2
,
3
)
14
calc(
1
,
3
,
5
,
7
)
84
|
所以,我们把函数的参数改为可变参数:
|
1
2
3
4
5
|
def
calc(
*
numbers):
sum
=
0
for
n
in
numbers:
sum
=
sum
+
n
*
n
return
sum
|
定义可变参数和定义一个list或tuple参数相比,仅仅在参数前面加了一个*号。在函数内部,参数numbers接收到的是一个tuple,因此,函数代码完全不变。但是,调用该函数时,可以传入任意个参数,包括0个参数:
|
1
2
3
4
|
calc(
1
,
2
)
5
calc()
0
|
如果已经有一个list或者tuple,要调用一个可变参数怎么办?可以这样做:
|
1
2
3
|
nums
=
[
1
,
2
,
3
]
calc(nums[
0
], nums[
1
], nums[
2
])
14
|
这种写法当然是可行的,问题是太繁琐,所以python允许你在list或tuple前面加一个*号,把list或tuple的元素变成可变参数传进去:
|
1
2
3
|
nums
=
[
1
,
2
,
3
]
calc(
*
nums)
14
|
*nums表示把nums这个list的所有元素作为可变参数传进去。这种写法相当有用,而且很常见.
以上这篇python 通过可变参数计算n个数的乘积方法就是小编分享给大家的全部内容了,希望能给大家一个参考,也希望大家多多支持我.
原文链接:https://blog.csdn.net/qq_36143023/article/details/78885504 。
最后此篇关于python 通过可变参数计算n个数的乘积方法的文章就讲到这里了,如果你想了解更多关于python 通过可变参数计算n个数的乘积方法的内容请搜索CFSDN的文章或继续浏览相关文章,希望大家以后支持我的博客! 。
我看到以下宏 here . static const char LogTable256[256] = { #define LT(n) n, n, n, n, n, n, n, n, n, n, n,
这个问题不太可能帮助任何 future 的访问者;它只与一个小的地理区域、一个特定的时间点或一个非常狭窄的情况有关,这些情况并不普遍适用于互联网的全局受众。为了帮助使这个问题更广泛地适用,visit
所以我得到了这个算法我需要计算它的时间复杂度 这样的 for i=1 to n do k=i while (k<=n) do FLIP(A[k]) k
n 的 n 次方(即 n^n)是多项式吗? T(n) = 2T(n/2) + n^n 可以用master方法求解吗? 最佳答案 它不仅不是多项式,而且比阶乘还差。 O(n^n) 支配 O(n!)。同样
我正在研究一种算法,它可以在带有变音符号的字符(tilde、circumflex、caret、umlaut、caron)及其“简单”字符之间进行映射。 例如: ń ǹ ň ñ ṅ ņ ṇ
嗯..我从昨天开始学习APL。我正在观看 YouTube 视频,从基础开始学习各种符号,我正在使用 NARS2000。 我想要的是打印斐波那契数列。我知道有好几种代码,但是因为我没有研究过高深的东西,
已关闭。这个问题是 off-topic 。目前不接受答案。 想要改进这个问题吗? Update the question所以它是on-topic用于堆栈溢出。 已关闭12 年前。 Improve th
谁能帮我从 N * N * N → N 中找到一个双射数学函数,它接受三个参数 x、y 和 z 并返回数字 n? 我想知道函数 f 及其反函数 f',如果我有 n,我将能够通过应用 f'(n) 来
场景: 用户可以在字符串格式的方程式中输入任意数量的括号对。但是,我需要检查以确保所有括号 ( 或 ) 都有一个相邻的乘数符号 *。因此 3( 应该是 3*( 和 )3 应该是 )*3。 我需要将所有
在 Java 中,表达式: n+++n 似乎评估为等同于: n++ + n 尽管 +n 是一个有效的一元运算符,其优先级高于 n + n 中的算术 + 运算符。因此编译器似乎假设运算符不能是一元运算符
当我阅读 this 问题我记得有人曾经告诉我(很多年前),从汇编程序的角度来看,这两个操作非常不同: n = 0; n = n - n; 这是真的吗?如果是,为什么会这样? 编辑: 正如一些回复所指出
我正在尝试在reveal.js 中加载外部markdown 文件,该文件已编写为遵守数据分隔符语法: You can write your content as a separate file and
我试图弄清楚如何使用 Javascript 生成一个随机 11 个字符串,该字符串需要特定的字母/数字序列,以及位置。 ----------------------------------------
我最近偶然发现了一个资源,其中 2T(n/2) + n/log n 类型 的递归被 MM 宣布为无法解决。 直到今天,当另一种资源被证明是矛盾的(在某种意义上)时,我才接受它作为引理。 根据资源(下面
关闭。此题需要details or clarity 。目前不接受答案。 想要改进这个问题吗?通过 editing this post 添加详细信息并澄清问题. 已关闭 8 年前。 Improve th
我完成的一个代码遵循这个模式: for (i = 0; i < N; i++){ // O(N) //do some processing... } sort(array, array + N
有没有办法证明 f(n) + g(n) = theta(n^2) 还是不可能?假设 f(n) = theta(n^2) & g(n) = O(n^2) 我尝试了以下方法:f(n) = O(n^2) &
所以我目前正在尝试计算我拥有的一些数据的 Pearson R 和 p 值。这是通过以下代码完成的: import numpy as np from scipy.stats import pearson
ltree 列的默认排序为文本。示例:我的表 id、parentid 和 wbs 中有 3 列。 ltree 列 - wbs 将 1.1.12, 1.1.1, 1.1.2 存储在不同的行中。按 wbs
我的目标是编写一个程序来计算在 python 中表示数字所需的位数,如果我选择 number = -1 或任何负数,程序不会终止,这是我的代码: number = -1 cnt = 0 while(n

我是一名优秀的程序员,十分优秀!