个人中心
gpt4 book ai didi

C++实现LeetCode(149.共线点个数)

转载 作者：qq735679552 更新时间：2022-09-27 22:32:09 30 4
gpt4 key购买 nike

CFSDN坚持开源创造价值，我们致力于搭建一个资源共享平台，让每一个IT人在这里找到属于你的精彩世界.

这篇CFSDN的博客文章C++实现LeetCode(149.共线点个数)由作者收集整理，如果你对这篇文章有兴趣，记得点赞哟.

[LeetCode] 149. Max Points on a Line 共线点个数

Given n points on a 2D plane, find the maximum number of points that lie on the same straight line. 。

Example 1

Input: [[1,1],[2,2],[3,3]] Output: 3 Explanation: ^ | |        o |     o |  o   +-------------> 0  1  2  3  4 。

Example 2

Input: [[1,1],[3,2],[5,3],[4,1],[2,3],[1,4]] Output: 4 Explanation: ^ | |  o |     o        o |        o |  o        o +-------------------> 0  1  2  3  4  5  6 。

这道题给了我们一堆二维点，然后让求最大的共线点的个数，根据初中数学可以知道，两点确定一条直线，而且可以写成 y = ax + b 的形式，所有共线的点都满足这个公式。所以这些给定点两两之间都可以算一个斜率，每个斜率代表一条直线，对每一条直线，带入所有的点看是否共线并计算个数，这是整体的思路。但是还有两点特殊情况需要考虑，一是当两个点重合时，无法确定一条直线，但这也是共线的情况，需要特殊处理。二是斜率不存在的情况，由于两个点 (x1, y1) 和 (x2, y2) 的斜率k表示为 (y2 - y1) / (x2 - x1)，那么当 x1 = x2 时斜率不存在，这种共线情况需要特殊处理。这里需要用到 TreeMap 来记录斜率和共线点个数之间的映射，其中第一种重合点的情况假定其斜率为 INT_MIN，第二种情况假定其斜率为 INT_MAX，这样都可以用 TreeMap 映射了。还需要顶一个变量 duplicate 来记录重合点的个数，最后只需和 TreeMap 中的数字相加即为共线点的总数，但这种方法现在已经无法通过 OJ 了，代码可以参见评论区八楼.

由于通过斜率来判断共线需要用到除法，而用 double 表示的双精度小数在有的系统里不一定准确，为了更加精确无误的计算共线，应当避免除法，从而避免无线不循环小数的出现，那么怎么办呢，这里把除数和被除数都保存下来，不做除法，但是要让这两数分别除以它们的最大公约数，这样例如8和4，4和2，2和1，这三组商相同的数就都会存到一个映射里面，同样也能实现目标，而求 GCD 的函数如果用递归来写那么一行就搞定了，叼不叼，这个方法能很好的避免除法的出现，算是牺牲了空间来保证精度吧，参见代码如下:

C++ 解法一:

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public :
     int maxPoints(vector<vector< int >>& points) {
         int res = 0;
         for ( int i = 0; i < points.size(); ++i) {
             map<pair< int , int >, int > m;
             int duplicate = 1;
             for ( int j = i + 1; j < points.size(); ++j) {
                 if (points[i][0] == points[j][0] && points[i][1] == points[j][1]) {
                     ++duplicate; continue ;
                 }
                 int dx = points[j][0] - points[i][0];
                 int dy = points[j][1] - points[i][1];
                 int d = gcd(dx, dy);
                 ++m[{dx / d, dy / d}];
             }
             res = max(res, duplicate);
             for (auto it = m.begin(); it != m.end(); ++it) {
                 res = max(res, it->second + duplicate);
             }
         }
         return res;
     }
     int gcd( int a, int b) {
         return (b == 0) ? a : gcd(b, a % b);
     }
};

Java 解法一:

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
     public int maxPoints( int [][] points) {
         int res = 0 ;
         for ( int i = 0 ; i < points.length; ++i) {
             Map<Map<Integer, Integer>, Integer> m = new HashMap<>();
             int duplicate = 1 ;
             for ( int j = i + 1 ; j < points.length; ++j) {
                 if (points[i][ 0 ] == points[j][ 0 ] && points[i][ 1 ] == points[j][ 1 ]) {
                     ++duplicate; continue ;
                 }
                 int dx = points[j][ 0 ] - points[i][ 0 ];
                 int dy = points[j][ 1 ] - points[i][ 1 ];
                 int d = gcd(dx, dy);
                 Map<Integer, Integer> t = new HashMap<>();
                 t.put(dx / d, dy / d);
                 m.put(t, m.getOrDefault(t, 0 ) + 1 );
             }
             res = Math.max(res, duplicate);
             for (Map.Entry<Map<Integer, Integer>, Integer> e : m.entrySet()) {
                 res = Math.max(res, e.getValue() + duplicate);
             }
         }
         return res;
     }
     public int gcd( int a, int b) {
         return (b == 0 ) ? a : gcd(b, a % b);
     }
}

令博主惊奇的是，这道题的 OJ 居然容忍 brute force 的方法通过，博主认为下面这种 O(n3) 的解法之所以能通过 OJ，可能还有一个原因就是用了比较高效的判断三点共线的方法。一般来说判断三点共线有三种方法，斜率法，周长法，面积法 。而其中通过判断叉积为零的面积法是坠好的。比如说有三个点 A(x1, y1)、B(x2, y2)、C(x3, y3)，那么判断三点共线就是判断下面这个等式是否成立:

C++实现LeetCode(149.共线点个数)

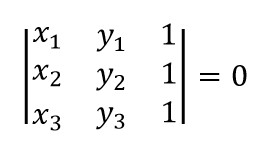
行列式的求法不用多说吧，不会的话回去翻线性代数，当初少打点刀塔不就好啦~ 。

C++ 解法二:

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public :
     int maxPoints(vector<vector< int >>& points) {
         int res = 0;
         for ( int i = 0; i < points.size(); ++i) {
             int duplicate = 1;
             for ( int j = i + 1; j < points.size(); ++j) {
                 int cnt = 0;
                 long long x1 = points[i][0], y1 = points[i][1];
                 long long x2 = points[j][0], y2 = points[j][1];
                 if (x1 == x2 && y1 == y2) {++duplicate; continue ;}
                 for ( int k = 0; k < points.size(); ++k) {
                     int x3 = points[k][0], y3 = points[k][1];
                     if (x1 * y2 + x2 * y3 + x3 * y1 - x3 * y2 - x2 * y1 - x1 * y3 == 0) {
                         ++cnt;
                     }
                 }
                 res = max(res, cnt);
             }
             res = max(res, duplicate);
         }
         return res;
     }
};

Java 解法二:

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
     public int maxPoints( int [][] points) {
         int res = 0 , n = points.length;
         for ( int i = 0 ; i < n; ++i) {
             int duplicate = 1 ;
             for ( int j = i + 1 ; j < n; ++j) {
                 int cnt = 0 ;
                 long x1 = points[i][ 0 ], y1 = points[i][ 1 ];
                 long x2 = points[j][ 0 ], y2 = points[j][ 1 ];
                 if (x1 == x2 && y1 == y2) {++duplicate; continue ;}
                 for ( int k = 0 ; k < n; ++k) {
                     int x3 = points[k][ 0 ], y3 = points[k][ 1 ];
                     if (x1*y2 + x2*y3 + x3*y1 - x3*y2 - x2*y1 - x1 * y3 == 0 ) {
                         ++cnt;
                     }
                 }
                 res = Math.max(res, cnt);
             }
             res = Math.max(res, duplicate);
         }
         return res;
     }
}

Github 同步地址:

https://github.com/grandyang/leetcode/issues/149 。

类似题目:

Line Reflection 。

参考资料:

https://leetcode.com/problems/max-points-on-a-line/ 。

https://leetcode.com/problems/max-points-on-a-line/discuss/221044/ 。

https://leetcode.com/problems/max-points-on-a-line/discuss/47113/A-java-solution-with-notes 。

https://leetcode.com/problems/max-points-on-a-line/discuss/47117/Sharing-my-simple-solution-with-explanation 。

到此这篇关于C++实现LeetCode(149.共线点个数)的文章就介绍到这了,更多相关C++实现共线点个数内容请搜索我以前的文章或继续浏览下面的相关文章希望大家以后多多支持我！ 。

原文链接：https://www.cnblogs.com/grandyang/p/4579693.html 。

最后此篇关于C++实现LeetCode(149.共线点个数)的文章就讲到这里了,如果你想了解更多关于C++实现LeetCode(149.共线点个数)的内容请搜索CFSDN的文章或继续浏览相关文章，希望大家以后支持我的博客！ 。

30 4 0
文章推荐： C++实现LeetCode(150.计算逆波兰表达式)
文章推荐： 详解VS2019 dumpbin查看DLL的导出函数
文章推荐： 深入理解Java定时调度(Timer)机制
文章推荐： Qt在vs2019中使用及设置方法
qq735679552
个人简介

我是一名优秀的程序员,十分优秀！

滴滴打车优惠券免费领取
滴滴打车优惠券
Copyright 2021 - 2024 cfsdn All Rights Reserved 蜀ICP备2022000587号
广告合作:1813099741@qq.com 6ren.com