- ubuntu12.04环境下使用kvm ioctl接口实现最简单的虚拟机
- Ubuntu 通过无线网络安装Ubuntu Server启动系统后连接无线网络的方法
- 在Ubuntu上搭建网桥的方法
- ubuntu 虚拟机上网方式及相关配置详解
CFSDN坚持开源创造价值,我们致力于搭建一个资源共享平台,让每一个IT人在这里找到属于你的精彩世界.
这篇CFSDN的博客文章浅谈Python数学建模之固定费用问题由作者收集整理,如果你对这篇文章有兴趣,记得点赞哟.
。
。
固定费用问题,是指求解生产成本最小问题时,总成本包括固定成本和变动成本,而选择不同生产方式会有不同的固定成本,因此总成本与选择的生产方式有关.
固定费用问题,实际上是互斥的目标函数问题,对于不同的生产方式具有多个互斥的目标函数,但只有一个起作用。固定费用问题不能用一般的线性规划模型求解.
一般地,设有 m 种生产方式可供选择,采用第 j 种方式时的固定成本为 (K_j)、变动成本为 (c_j)、产量为 (x_j),则采用各种生产方式的总成本分别为:
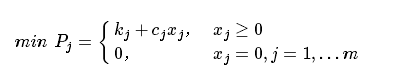
该类问题的建模方法,为了构造统一的目标函数,可以引入 m 个 0-1 变量 y_j 表示是否采用第 j 种生产方式:

于是可以构造新的目标函数和约束条件:
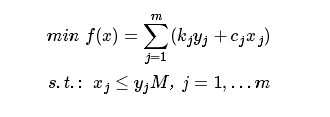
M 是一个充分大的常数.
。
例题 1:
某服装厂可以生产 A、B、C 三种服装,生产不同种类服装需要租用不同设备,设备租金、生产成本、销售价格等指标如下表所示.
| 服装种类 | 设备租金 | 材料成本 | 销售价格 | 人工工时 | 设备工时 | 设备可用工时 |
|---|---|---|---|---|---|---|
| 单位 | (元) | (元/件) | (元/件) | (小时/件) | (小时/件) | (小时) |
| A | 5000 | 280 | 400 | 5 | 3 | 300 |
| B | 2000 | 30 | 40 | 1 | 0.5 | 300 |
| C | 2000 | 200 | 300 | 4 | 2 | 300 |
如果各类服装的市场需求都足够大,服装厂每月可用人工时为 2000h,那么应该如何安排生产计划使利润最大?
。
首先要理解生产某种服装就会发生设备租金,租金只与是否生产该产品有关,而与生产数量无关,这就是固定成本。因此本题属于固定费用问题.
有些同学下意识地认为是从 3 种产品中选择一种,但题目中并没有限定必须或只能生产一种产品,因此决策结果可以是都不生产、选择 1 种或 2 种产品、3 种都生产.
决策结果会是什么都不生产吗?有可能的.
每种产品的利润:(销售价格 - 材料成本)× 生产数量 - 设备租金 。
本题中如果设备租金很高,决策结果就可能是什么都不做时利润最大,这是利润为 0,至少不亏.
现在可以用固定费用问题的数学模型来描述问题了:

。
编程求解建立的数学模型,用标准模型的优化算法对模型求解,得到优化结果.
模型求解的编程步骤与之前的线性规划、整数规划问题并没有什么区别,这就是 PuLP工具包的优势.
(0)导入 PuLP库函数 。
import pulp
(1)定义一个规划问题 。
FixedCostP1 = pulp.LpProblem("Fixed_cost_problem", sense=pulp.LpMaximize) # 定义问题,求最大值
pulp.LpProblem 用来定义问题的构造函数。"FixedCostP1"是用户定义的问题名。 参数 sense 指定问题求目标函数的最小值/最大值 。本例求最大值,选择 “pulp.LpMaximize” .
(2)定义决策变量 。
x1 = pulp.LpVariable("A", cat="Binary") # 定义 x1,0-1变量,是否生产 A 产品x2 = pulp.LpVariable("B", cat="Binary") # 定义 x2,0-1变量,是否生产 B 产品x3 = pulp.LpVariable("C", cat="Binary") # 定义 x3,0-1变量,是否生产 C 产品y1 = pulp.LpVariable("yieldA", lowBound=0, upBound=100, cat="Integer") # 定义 y1,整型变量y2 = pulp.LpVariable("yieldB", lowBound=0, upBound=600, cat="Integer") # 定义 y2,整型变量y3 = pulp.LpVariable("youCans", lowBound=0, upBound=150, cat="Integer") # 定义 y3,整型变量
pulp.LpVariable 用来定义决策变量的函数。参数 cat 用来设定变量类型," Binary " 表示0/1变量(用于0/1规划问题)," Integer " 表示整数变量。"lowBound"、"upBound" 分别表示变量取值范围的下限和上限.
(3)添加目标函数 。
FixedCostP1 += pulp.lpSum(-5000*x1-2000*x2-2000*x3+120*y1+10*y2+100*y3) # 设置目标函数 f(x)
(4)添加约束条件 。
FixedCostP1 += (5*y1 + y2 + 4*y3 <= 2000) # 不等式约束FixedCostP1 += (3*y1 - 300*x1 <= 0) # 不等式约束FixedCostP1 += (0.5*y2 - 300*x2 <= 0) # 不等式约束FixedCostP1 += (2*y3 - 300*x3 <= 0) # 不等式约束
添加约束条件使用 "问题名 += 约束条件表达式" 格式。 约束条件可以是等式约束或不等式约束,不等式约束可以是 小于等于 或 大于等于,分别使用关键字">="、"<="和"==".
(5)求解 。
FixedCostP1.solve()
solve() 是求解函数,可以对求解器、求解精度进行设置.
。
import pulp # 导入 pulp 库# 主程序def main(): # 固定费用问题(Fixed cost problem) print("固定费用问题(Fixed cost problem)") # 问题建模: """ 决策变量: y(i) = 0, 不生产第 i 种产品 y(i) = 1, 生产第 i 种产品 x(i), 生产第 i 种产品的数量, i>=0 整数 i=1,2,3 目标函数: min profit = 120x1 + 10x2+ 100x3 - 5000y1 - 2000y2 - 2000y3 约束条件: 5x1 + x2 + 4x3 <= 2000 3x1 <= 300y1 0.5x2 <= 300y2 2x3 <= 300y3 变量取值范围:Youcans XUPT 0<=x1<=100, 0<=x2<=600, 0<=x3<=150, 整数变量 y1, y2 ,y3 为 0/1 变量 """ # 1. 固定费用问题(Fixed cost problem), 使用 PuLP 工具包求解 # (1) 建立优化问题 FixedCostP1: 求最大值(LpMaximize) FixedCostP1 = pulp.LpProblem("Fixed_cost_problem_1", sense=pulp.LpMaximize) # 定义问题,求最大值 # (2) 建立变量 x1 = pulp.LpVariable("A", cat="Binary") # 定义 x1,0-1变量,是否生产 A 产品 x2 = pulp.LpVariable("B", cat="Binary") # 定义 x2,0-1变量,是否生产 B 产品 x3 = pulp.LpVariable("C", cat="Binary") # 定义 x3,0-1变量,是否生产 C 产品 y1 = pulp.LpVariable("yieldA", lowBound=0, upBound=100, cat="Integer") # 定义 y1,整型变量 y2 = pulp.LpVariable("yieldB", lowBound=0, upBound=600, cat="Integer") # 定义 y2,整型变量 y3 = pulp.LpVariable("yieldC", lowBound=0, upBound=150, cat="Integer") # 定义 y3,整型变量 # (3) 设置目标函数 FixedCostP1 += pulp.lpSum(-5000*x1-2000*x2-2000*x3+120*y1+10*y2+100*y3) # 设置目标函数 f(x) # (4) 设置约束条件 FixedCostP1 += (5*y1 + y2 + 4*y3 <= 2000) # 不等式约束 FixedCostP1 += (3*y1 - 300*x1 <= 0) # 不等式约束 FixedCostP1 += (0.5*y2 - 300*x2 <= 0) # 不等式约束 FixedCostP1 += (2*y3 - 300*x3 <= 0) # 不等式约束 # (5) 求解 youcans FixedCostP1.solve() # (6) 打印结果 print(FixedCostP1.name) if pulp.LpStatus[FixedCostP1.status] == "Optimal": # 获得最优解 for v in FixedCostP1.variables(): # youcans print(v.name, "=", v.varValue) # 输出每个变量的最优值 print("Youcans F(x) = ", pulp.value(FixedCostP1.objective)) # 输出最优解的目标函数值 returnif __name__ == "__main__": # Copyright 2021 YouCans, XUPT main()
。
Welcome to the CBC MILP Solver 。
Version: 2.9.0 。
Build Date: Feb 12 2015 。
。
Result - Optimal solution found 。
。
Fixed_cost_problem_1 。
A = 1.0 。
B = 1.0 。
C = 1.0 。
yieldA = 100.0 。
yieldB = 600.0 。
yieldC = 150.0 。
Max F(x) = 24000.0 。
从固定费用问题模型的求解结果可知,A、B、C 三种服装都生产,产量分别为 A/100、B/600、C/150 时获得最大利润为:24000.
。
。
通过从线性规划、整数规划、0-1规划到上例中的混合0-1规划问题,我们已经充分体会到 PuLP 使用相同的步骤和参数处理不同问题所带来的便利.
但是,如果问题非常复杂,例如变量数量很多,约束条件复杂,逐个定义变量、逐项编写目标函数与约束条件的表达式,不仅显得重复冗长,不方便修改对变量和参数的定义,而且在输入过程中容易发生错误。因此,我们希望用字典、列表、循环等快捷方法来进行变量定义、目标函数和约束条件设置.
PuLP 提供了快捷建模的编程方案,下面我们仍以上节中的固定费用问题为例进行介绍。本例中的问题、条件和参数都与上节完全相同,以便读者进行对照比较快捷方法的具体内容.
(0)导入 PuLP 库函数 。
import pulp
(1)定义一个规划问题 。
FixedCostP2 = pulp.LpProblem("Fixed_cost_problem", sense=pulp.LpMaximize) # 定义问题,求最大值
(2)定义决策变量 。
types = ["A", "B", "C"] # 定义产品种类status = pulp.LpVariable.dicts("生产决策", types, cat="Binary") # 定义 0/1 变量,是否生产该产品yields = pulp.LpVariable.dicts("生产数量", types, lowBound=0, upBound=600, cat="Integer") # 定义整型变量
本例中的快捷方法使用列表 types 定义 0/1 变量 status 和 整型变量 yields,不论产品的品种有多少,都只有以上几句,从而使程序大为简化.
(3)添加目标函数 。
fixedCost = {"A":5000, "B":2000, "C":2000} # 各产品的 固定费用unitProfit = {"A":120, "B":10, "C":100} # 各产品的 单位利润FixedCostP2 += pulp.lpSum([(yields[i]*unitProfit[i]- status[i]*fixedCost[i]) for i in types])
虽然看起来本例中定义目标函数的程序语句较长,但由于使用字典定义参数、使用 for 循环定义目标函数,因此程序更加清晰、简明、便于修改参数、不容易输入错误.
(4)添加约束条件 。
humanHours = {"A":5, "B":1, "C":4} # 各产品的 单位人工工时machineHours = {"A":3.0, "B":0.5, "C":2.0} # 各产品的 单位设备工时maxHours = {"A":300, "B":300, "C":300} # 各产品的 最大设备工时FixedCostP2 += pulp.lpSum([humanHours[i] * yields[i] for i in types]) <= 2000 # 不等式约束for i in types: FixedCostP2 += (yields[i]*machineHours[i] - status[i]*maxHours[i] <= 0) # 不等式约束
快捷方法对于约束条件的定义与对目标函数的定义相似,使用字典定义参数,使用循环定义约束条件,使程序简单、结构清楚.
注意本例使用了两种不同的循环表达方式:语句内使用 for 循环遍历列表实现所有变量的线性组合,标准的 for 循环结构实现多组具有相似结构的约束条件。读者可以对照数学模型及上例的例程,理解这两种定义约束条件的快捷方法.
(5)求解和结果的输出 。
# (5) 求解FixedCostP2.solve()# (6) 打印结果print(FixedCostP2.name)temple = "品种 %(type)s 的决策是:%(status)s,生产数量为:%(yields)d"if pulp.LpStatus[FixedCostP2.status] == "Optimal": # 获得最优解 for i in types: output = {"type": i, "status": "同意" if status[i].varValue else "否决", "yields": yields[i].varValue} print(temple % output) # youcans@qq.com print("最大利润 = ", pulp.value(FixedCostP2.objective)) # 输出最优解的目标函数值
由于快捷方法使用列表或字典定义变量,对求解的优化结果也便于实现结构化的输出.
。
import pulp # 导入 pulp 库# 主程序def main(): # 2. 问题同上,PuLP 快捷方法示例 # (1) 建立优化问题 FixedCostP2: 求最大值(LpMaximize) FixedCostP2 = pulp.LpProblem("Fixed_cost_problem_2", sense=pulp.LpMaximize) # 定义问题,求最大值 # (2) 建立变量 types = ["A", "B", "C"] # 定义产品种类 status = pulp.LpVariable.dicts("生产决策", types, cat="Binary") # 定义 0/1 变量,是否生产该产品 yields = pulp.LpVariable.dicts("生产数量", types, lowBound=0, upBound=600, cat="Integer") # 定义整型变量 # (3) 设置目标函数 fixedCost = {"A":5000, "B":2000, "C":2000} # 各产品的 固定费用 unitProfit = {"A":120, "B":10, "C":100} # 各产品的 单位利润 FixedCostP2 += pulp.lpSum([(yields[i]*unitProfit[i]- status[i]*fixedCost[i]) for i in types]) # (4) 设置约束条件 humanHours = {"A":5, "B":1, "C":4} # 各产品的 单位人工工时 machineHours = {"A":3.0, "B":0.5, "C":2.0} # 各产品的 单位设备工时 maxHours = {"A":300, "B":300, "C":300} # 各产品的 最大设备工时 FixedCostP2 += pulp.lpSum([humanHours[i] * yields[i] for i in types]) <= 2000 # 不等式约束 for i in types: FixedCostP2 += (yields[i]*machineHours[i] - status[i]*maxHours[i] <= 0) # 不等式约束 # (5) 求解 youcans FixedCostP2.solve() # (6) 打印结果 print(FixedCostP2.name) temple = "品种 %(type)s 的决策是:%(status)s,生产数量为:%(yields)d" if pulp.LpStatus[FixedCostP2.status] == "Optimal": # 获得最优解 for i in types: output = {"type": i, "status": "同意" if status[i].varValue else "否决", "yields": yields[i].varValue} print(temple % output) print("最大利润 = ", pulp.value(FixedCostP2.objective)) # 输出最优解的目标函数值 returnif __name__ == "__main__": # Copyright 2021 YouCans, XUPT main()
。
Welcome to the CBC MILP Solver 。
Version: 2.9.0 。
Build Date: Feb 12 2015 。
。
Result - Optimal solution found 。
。
Fixed_cost_problem_2 。
品种 A 的决策是:同意,生产数量为:100 。
品种 B 的决策是:同意,生产数量为:600 。
品种 C 的决策是:同意,生产数量为:150 。
最大利润 = 24000.0 。
本例的问题、条件和参数都与上节完全相同,只是采用 PuLP 提供的快捷建模的编程方案,优化结果也与 PuLP 标准方法完全相同,但本例使用了结构化的输出显示,使输出结果更为直观.
以上就是浅谈Python数学建模之固定费用问题的详细内容,更多关于Python 数学建模 固定费用的资料请关注我其它相关文章! 。
原文链接:https://www.cnblogs.com/youcans/p/14872211.html 。
最后此篇关于浅谈Python数学建模之固定费用问题的文章就讲到这里了,如果你想了解更多关于浅谈Python数学建模之固定费用问题的内容请搜索CFSDN的文章或继续浏览相关文章,希望大家以后支持我的博客! 。
我正在尝试实现 3 列固定-流体-固定布局。此外,布局的高度必须占据整个屏幕,使其看起来像从上到下的 3 个实心列。 总结: Left-column: fixed-width Center-col
我在网上搜索过,似乎找不到一个干净、简单、所有浏览器都友好的 3 列布局。 我希望有 3 列布局,左列固定为 200px,右列固定为 200px,中间列为剩余宽度,但最小宽度为 600px。所以整体最
关闭。这个问题需要更多focused .它目前不接受答案。 想改进这个问题吗? 更新问题,使其只关注一个问题 editing this post . 关闭 8 年前。 Improve this q
我正在使用一些音频指纹技术来标记长录音中的歌曲。例如,在广播节目中的记录。指纹机制工作正常,但我在归一化(或下采样)方面遇到问题。 在这里您可以看到两首相同的歌曲,但波形不同。我知道我应该进行一些直流
为什么使用cout调用setprecision和fixed以及其他iomanip函数不像例如name.find('')plz这样的字符串函数 最佳答案 它们允许您以以下方式链接操作: cout <<
我正在尝试创建一个侧边栏,当用户向下滚动页面时,该侧边栏会跟随用户,并且我设法使用以下代码实现了效果: 标记 Javas
我正在尝试设置一些性能分析以及影响缓冲策略的运行时决策。我的应用程序收到一个指向由库(CUDA 或 OpenCL)分配的缓冲区的指针。 如何测试内存区域是否被页面锁定? 据我所知,POSIX 给了我们
我正在用 C# 编写一个 B+ 树实现,我为我的应用程序选择的树实现有一个非常特定的结构,它是缓存敏感的。为了实现这些属性,它对树节点有严格的布局策略。 我想要的只是使用 C# 的 fixed 来表达
我试图通过将 fragment 注入(inject)容器来在每个屏幕的底部放置一个广告 View 。通过使用 LinearLayout,我可以将 adview 置于操作栏下方的顶部。我已经尝试了 Re
我正在尝试创建一个导航稍微复杂的网站。我已经让导航看起来像我想要的初始加载,但现在我试图让它粘性导航到滚动顶部。我已经能够在导航栏到达顶部时创建一个类,但无法使其粘滞。每次我添加一个位置时,它都会跳回
首先,我正在寻找一个纯 CSS 解决方案。我可以使用 JavaScript 非常轻松地做到这一点,所以不要费心给我提示如何在 JS 中做到这一点。 我有一个包含 3 个容器的网页。其中 2 个是固定的
我猜这里有一种 super 特例。 我正在处理许多包含。现在我正在一个包含的内容文件中编码。我需要一个灯箱,它有一个 20% 的黑色背景覆盖整个页面,包括本身固定的标题,并在先前的 PHP 文件中设置
我正在尝试制作一个包含两个“固定”侧边栏图像和一个“固定”标题图像的页面。由于标题是固定的(距顶部 0 到 10%)。我不希望页眉图像与页面上的任何文本重叠。我尝试将段落标记定位为“相对”,并将其设置
我遇到了一个(水平)居中固定位置元素的解决方案,如下所示: element { width: 200px; position: fixed; left: 0; righ
我试图让我的网站主体具有固定的高度(我想!)。 无论如何,站点正文只是白色,边框大小为 1。基本上,正文的大小取决于其中的内容,例如,随着添加更多内容,它会自动调整大小。 我想要的是垂直滚动条,这样主
是否可以在 css 中创建 master-detail-states 布局? 我需要 3 个占位符: +---------------+-------+ | A | B
我的问题是,我是否必须在每个 Get/Post 请求之前单独请求检查 SSL Pinning OkHttpClient client = new OkHttpClient.Builder().cert
假设我有一个具有 N 个节点的常量(一旦构建就不会改变)平衡树,每个内部节点都有 p 个子节点。显然,访问节点的最坏情况是 logp(N)。但是访问 r 个节点的摊销成本呢?如果我们按升序访问它们(有
我知道会话固定是用php破解网站的方法。 会话固定是一种允许攻击者劫持有效用户会话的攻击 session fixation 但我不知道这可以防止我的项目中出现此问题。 是描述解决方案的方式或样本。 最
我在 jquery 砖石布局内有一个导航元素,我想将其修复到特定位置,比如右上角。是否可以这样做,以便所有其他元素都位于它周围? 诸如前置导航之类的东西.. 这是我的代码:http://jsfiddl

我是一名优秀的程序员,十分优秀!