个人中心
gpt4 book ai didi

c语言数据结构之并查集 总结

转载 作者：qq735679552 更新时间：2022-09-28 22:32:09 29 4
gpt4 key购买 nike

CFSDN坚持开源创造价值，我们致力于搭建一个资源共享平台，让每一个IT人在这里找到属于你的精彩世界.

这篇CFSDN的博客文章c语言数据结构之并查集 总结由作者收集整理，如果你对这篇文章有兴趣，记得点赞哟.

并查集(Union-Find Set):

一种用于管理分组的数据结构。它具备两个操作：(1)查询元素a和元素b是否为同一组 (2) 将元素a和b合并为同一组.

注意：并查集不能将在同一组的元素拆分为两组.

并查集的实现:

用树来实现.

c语言数据结构之并查集 总结

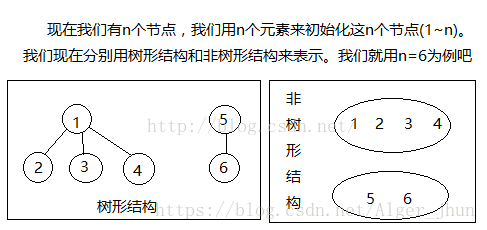
使用树形结构来表示以后，每一组都对应一棵树，然而我们就可以将这个问题转化为树的问题了，我们看两个元素是否为一组我们只要看这两个元素的根是否一致。显然，使用树形结构将问题简单化了。合并时是我们只需要将一组的根与另一组的根相连即可.

并查集的核心在于，一棵树的所有节点根节点都为一个节点。使用Find函数查询时，也是查询到这个节点的根节点.

一行并查集:

?
1
2
3
4
int find( int x)
{
  return p[x]==x? x:find(p[x]); //x的父节点保存在p[x]中，如果没有父节点则p[x]=x。
}

实现:

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
int node[i]; //每个节点
 
//初始化n个节点
void Init( int n){
  for ( int i = 0; i < n; i++){
  node[i] = i;
  }
}
//查找当前元素所在树的根节点(代表元素)
int find( int x){
  if (x == node[x])
  return x;
  return find(node[x]);
}
//合并元素x， y所处的集合
void Unite( int x, int y){
  //查找到x，y的根节点
  x = find(x);
  y = find(y);
  if (x == y)
  return ;
  //将x的根节点与y的根节点相连
  node[x] = y;
}
//判断x，y是属于同一个集合
bool same( int x, int y){
  return find(x) == find(y)

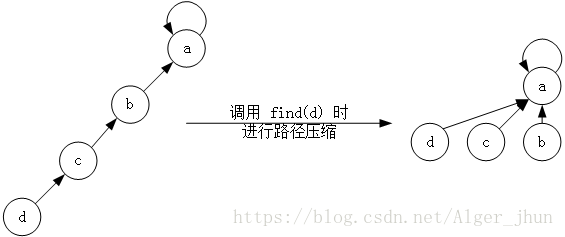
并查集的路径压缩:

在特殊情况下，这棵树是一条长长的树链，设链的最后一个结点为x，则每次执行find(x)都会遍历整条链。效率十分的地下。 改进方法很简单，只要把遍历过的结点都改成根的子结点，后面的查询就会变的快很多.

c语言数据结构之并查集 总结

并查集的复杂度 。

加入这两个优化之后，并查集的效率就非常高。对n个元素的并查集操作一次的复杂度是： O(α(n))。这里，α(n)是阿克曼(Ackermann)函数的反函数。效率要高于O(log n).

不过这里O(α(n))是平均复杂度。也就是说，多次操作之后平均复杂度为O(α(n))，换而言之，并不是每一次操作都满足O(α(n)).

路径压缩后的优化代码:

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
int node[i]; //每个节点
int rank[i]; //树的高度
 
//初始化n个节点
void Init( int n){
for ( int i = 0; i < n; i++){
  node[i] = i;
  rank[i] = 0;
}
}
//查找当前元素所在树的根节点(代表元素)
int find( int x){
if (x == node[x])
  return x;
return node[x] = find(node[x]); //在第一次查找时，将节点直连到根节点
}
//合并元素x， y所处的集合
void Unite( int x, int y){
//查找到x，y的根节点
x = find(x);
y = find(y);
if (x == y)
  return ;
//判断两棵树的高度，然后在决定谁为子树
if (rank[x] < rank[y]){
  node[x] = y;
} else {
  node[y] = x;
  if (rank[x] == rank[y]) rank[x]++:
}
}
//判断x，y是属于同一个集合
bool same( int x, int y){
return find(x) == find(y);
}

实例分析:

题目：部落 。

在一个社区里，每个人都有自己的小圈子，还可能同时属于很多不同的朋友圈。我们认为朋友的朋友都算在一个部落里，于是要请你统计一下，在一个给定社区中，到底有多少个互不相交的部落？并且检查任意两个人是否属于同一个部落.

输入格式:

输入在第一行给出一个正整数N（<= 104），是已知小圈子的个数。随后N行，每行按下列格式给出一个小圈子里的人:

K P[1] P[2] ... P[K] 。

其中K是小圈子里的人数，P[i]（i=1, .., K）是小圈子里每个人的编号。这里所有人的编号从1开始连续编号，最大编号不会超过104.

之后一行给出一个非负整数Q（<= 104），是查询次数。随后Q行，每行给出一对被查询的人的编号.

输出格式:

首先在一行中输出这个社区的总人数、以及互不相交的部落的个数。随后对每一次查询，如果他们属于同一个部落，则在一行中输出“Y”，否则输出“N”.

输入样例： 4 3 10 1 2 2 3 4 4 1 5 7 8 3 9 6 4 2 10 5 3 7 。

输出样例:

10 2 Y N 。

分析：典型并查集问题.

一个部落对应一个集合。 根节点数量等于部落数量。 并查集把每个部落的人连起来，记录哪些人出现过，枚举标号10000，找出有多少人和部落，查询并查集维护.

源码分析:

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;
int pre[10005];
int f[10005];
 
void init() { //初始化父集合pre[10005]，以及出现的标志数组f[10005]
     for ( int i=0; i<10004; i++)
         pre[i]=i, f[i]=0;
}
 
int find( int x) { //并查集查找根节点的 递归程序
     return pre[x]==x? x : pre[x]=find(pre[x]);
}
 
int main()
{
     init();
     int n,q,k,a,b;
     cin>>n;
     for ( int i=0; i<n; i++) {
         cin>>k>>a;
         f[a]=1;
         for ( int j=1; j<k; j++) {
             cin>>b;
             f[b]=1;
             int x=find(a);
             int y=find(b);
             if (x!=y) pre[x]=y;
         }
     }
     int cnt=0,tot=0; //cnt为所有人数 tot为部落数量
     for ( int i=0; i<10004; i++) {
         if (f[i] == 1) { //如果标志为1 则说明出现过，cnt加一
             cnt++;
             if (pre[i]==i) tot++; //如果下标为本身 说明其为根节点 根节点数量为部落的数量
         }
     }
     cout<<cnt<< " " <<tot<<endl;
     cin>>q;
     for ( int i=0; i<q; i++) {
         cin>>a>>b;
         if (find(a) == find(b)) //若两参数 有同一根节点 说明为一个部落。
             cout<< "Y" <<endl;
         else cout<< "N" <<endl;
     }
     return 0;
}

好了，这篇文章就介绍到这了.

原文链接：https://blog.csdn.net/Alger_jhun/article/details/79730169 。

最后此篇关于c语言数据结构之并查集 总结的文章就讲到这里了,如果你想了解更多关于c语言数据结构之并查集 总结的内容请搜索CFSDN的文章或继续浏览相关文章，希望大家以后支持我的博客！ 。

29 4 0
文章推荐： 霸气十足的男生昵称很简短 洒脱很帅的男生昵称合集
文章推荐： vue 修改 data 数据问题并实时显示操作
文章推荐： nginx部署多个vue项目的方法示例
文章推荐： js实现简单的无缝轮播效果
qq735679552
个人简介

我是一名优秀的程序员,十分优秀！

滴滴打车优惠券免费领取
滴滴打车优惠券
Copyright 2021 - 2024 cfsdn All Rights Reserved 蜀ICP备2022000587号
广告合作:1813099741@qq.com 6ren.com