- ubuntu12.04环境下使用kvm ioctl接口实现最简单的虚拟机
- Ubuntu 通过无线网络安装Ubuntu Server启动系统后连接无线网络的方法
- 在Ubuntu上搭建网桥的方法
- ubuntu 虚拟机上网方式及相关配置详解
CFSDN坚持开源创造价值,我们致力于搭建一个资源共享平台,让每一个IT人在这里找到属于你的精彩世界.
这篇CFSDN的博客文章golang 实现菜单树的生成方式由作者收集整理,如果你对这篇文章有兴趣,记得点赞哟.
golang 实现菜单树的生成,包括菜单节点的选中状态、半选中状态,菜单的搜索.
1 该包提供两个方法根接口。
1.1 GenerateTree(nodes, selectedNodes []INode) (trees []Tree) 。
GenerateTree 自定义的结构体实现 INode 接口后调用此方法生成树结构.
1.2 FindRelationNode(nodes, allNodes []INode) (respNodes []INode)FindRelationNode 在 allTree 中查询 nodes 中节点的所有父子节点 返回 respNodes(包含 nodes , 跟其所有父子节点) 。
1.3 接口 INode|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
// ConvertToINodeArray 其他的结构体想要生成菜单树,直接实现这个接口
type INode interface {
// GetTitle 获取显示名字
GetTitle() string
// GetId获取id
GetId() int
// GetFatherId 获取父id
GetFatherId() int
// GetData 获取附加数据
GetData() interface{}
// IsRoot 判断当前节点是否是顶层根节点
IsRoot() bool
}
|
。
|
1
|
go get github.com/azhengyongqin/golang-tree-menu
|
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
|
// 定义我们自己的菜单对象
type SystemMenu struct {
Id int `json:"id"` //id
FatherId int `json:"father_id"` //上级菜单id
Name string `json:"name"` //菜单名
Route string `json:"route"` //页面路径
Icon string `json:"icon"` //图标路径
}
func (s SystemMenu) GetTitle() string {
return s.Name
}
func (s SystemMenu) GetId() int {
return s.Id
}
func (s SystemMenu) GetFatherId() int {
return s.FatherId
}
func (s SystemMenu) GetData() interface{} {
return s
}
func (s SystemMenu) IsRoot() bool {
// 这里通过FatherId等于0 或者 FatherId等于自身Id表示顶层根节点
return s.FatherId == 0 || s.FatherId == s.Id
}
|
|
1
2
3
4
5
6
7
8
|
type SystemMenus []SystemMenu
// ConvertToINodeArray 将当前数组转换成父类 INode 接口 数组
func (s SystemMenus) ConvertToINodeArray() (nodes []INode) {
for _, v := range s {
nodes = append(nodes, v)
}
return
}
|
。
3.1 添加测试数据|
1
2
3
4
5
6
7
8
9
10
11
|
// 模拟获取数据库中所有菜单,在其它所有的查询中,也是首先将数据库中所有数据查询出来放到数组中,
// 后面的遍历递归,都在这个 allMenu中进行,而不是在数据库中进行递归查询,减小数据库压力。
allMenu := []SystemMenu{
{Id: 1, FatherId: 0, Name: "系统总览", Route: "/systemOverview", Icon: "icon-system"},
{Id: 2, FatherId: 0, Name: "系统配置", Route: "/systemConfig", Icon: "icon-config"},
{Id: 3, FatherId: 1, Name: "资产", Route: "/asset", Icon: "icon-asset"},
{Id: 4, FatherId: 1, Name: "动环", Route: "/pe", Icon: "icon-pe"},
{Id: 5, FatherId: 2, Name: "菜单配置", Route: "/menuConfig", Icon: "icon-menu-config"},
{Id: 6, FatherId: 3, Name: "设备", Route: "/device", Icon: "icon-device"},
{Id: 7, FatherId: 3, Name: "机柜", Route: "/device", Icon: "icon-device"},
}
|
|
1
2
3
4
|
// 生成完全树
resp := GenerateTree(SystemMenus.ConvertToINodeArray(allMenu), nil)
bytes, _ := json.MarshalIndent(resp, "", "\t")
fmt.Println(string(bytes))
|
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
|
[
{
"title": "系统总览",
"leaf": false,
"checked": false,
"partial_selected": false,
"children": [
{
"title": "资产",
"leaf": false,
"checked": false,
"partial_selected": false,
"children": [
{
"title": "设备",
"leaf": true,
"checked": false,
"partial_selected": false,
"children": null
},
{
"title": "机柜",
"leaf": true,
"checked": false,
"partial_selected": false,
"children": null
}
]
},
{
"title": "动环",
"leaf": true,
"checked": false,
"partial_selected": false,
"children": null
}
]
},
{
"title": "系统配置",
"leaf": false,
"checked": false,
"partial_selected": false,
"children": [
{
"title": "菜单配置",
"leaf": true,
"checked": false,
"partial_selected": false,
"children": null
}
]
}
]
|

|
1
2
3
4
5
|
// 模拟选中 '资产' 菜单
selectedNode := []SystemMenu{allMenu[2]}
resp = GenerateTree(SystemMenus.ConvertToINodeArray(allMenu), SystemMenus.ConvertToINodeArray(selectedNode))
bytes, _ = json.Marshal(resp)
fmt.Println(string(pretty.Color(pretty.PrettyOptions(bytes, pretty.DefaultOptions), nil)))
|

|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
|
[
{
"title": "系统总览",
"leaf": false,
"checked": false,
"partial_selected": true,
"children": [
{
"title": "资产",
"leaf": false,
"checked": true,
"partial_selected": false,
"children": [
{
"title": "设备",
"leaf": true,
"checked": true,
"partial_selected": false,
"children": null
},
{
"title": "机柜",
"leaf": true,
"checked": true,
"partial_selected": false,
"children": null
}
]
},
{
"title": "动环",
"leaf": true,
"checked": false,
"partial_selected": false,
"children": null
}
]
},
{
"title": "系统配置",
"leaf": false,
"checked": false,
"partial_selected": false,
"children": [
{
"title": "菜单配置",
"leaf": true,
"checked": false,
"partial_selected": false,
"children": null
}
]
}
]
|
|
1
2
3
4
5
6
7
|
// 模拟从数据库中查询出 '设备'
device := []SystemMenu{allMenu[5]}
// 查询 `设备` 的所有父节点
respNodes := FindRelationNode(SystemMenus.ConvertToINodeArray(device), SystemMenus.ConvertToINodeArray(allMenu))
resp = GenerateTree(respNodes, nil)
bytes, _ = json.Marshal(resp)
fmt.Println(string(pretty.Color(pretty.PrettyOptions(bytes, pretty.DefaultOptions), nil)))
|

|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
[
{
"title": "系统总览",
"leaf": false,
"checked": false,
"partial_selected": false,
"children": [
{
"title": "资产",
"leaf": false,
"checked": false,
"partial_selected": false,
"children": [
{
"title": "设备",
"leaf": true,
"checked": false,
"partial_selected": false,
"children": null
}
]
}
]
}
]
|
源码地址:https://github.com/azhengyongqin/golang-tree-menu 。
补充:golang实现prim算法,计算最小生成树 。
。
给定一个n个点m条边的无向图,图中可能存在重边和自环,边权可能为负数.
求最小生成树的树边权重之和,如果最小生成树不存在则输出impossible.
给定一张边带权的无向图G=(V, E),其中V表示图中点的集合,E表示图中边的集合,n=|V|,m=|E|.
由V中的全部n个顶点和E中n-1条边构成的无向连通子图被称为G的一棵生成树,其中边的权值之和最小的生成树被称为无向图G的最小生成树.
输入格式 。
第一行包含两个整数n和m.
接下来m行,每行包含三个整数u,v,w,表示点u和点v之间存在一条权值为w的边.
输出格式 。
共一行,若存在最小生成树,则输出一个整数,表示最小生成树的树边权重之和,如果最小生成树不存在则输出impossible.
。
数据范围 。
1≤n≤500.
1≤m≤105.
图中涉及边的边权的绝对值均不超过10000.
输入样例:
4 5 。
1 2 1 。
1 3 2 。
1 4 3 。
2 3 2 。
3 4 4 。
输出样例:
6 。
数据图 。
1、初始所有点的距离为正无穷,就是代码中的0x3f3f3f3f等于1061109567 。
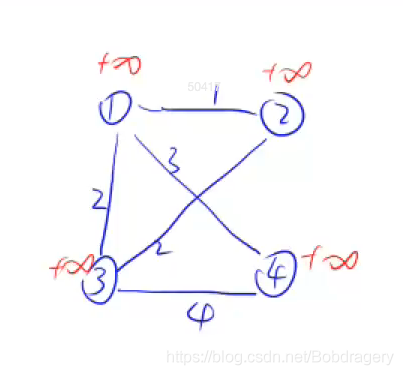
2、以第一个点为最初点,绿色表示选中,进入到最小生成树中 。
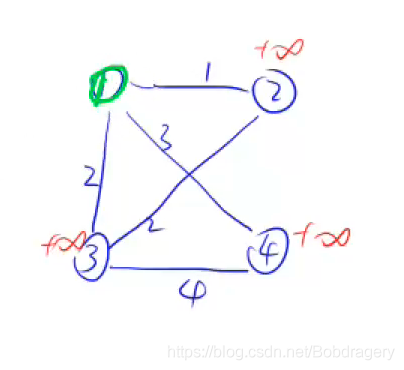
3、以第一个更新其他与之连通的点的距离 。
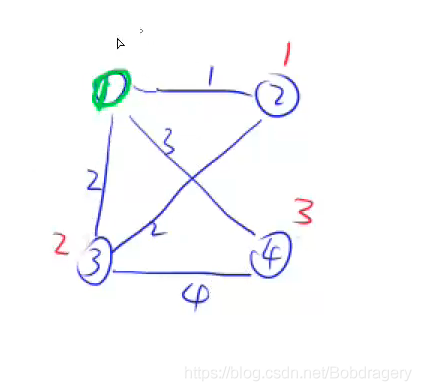
4、依次迭代 。
5、最后的最小生成树 。
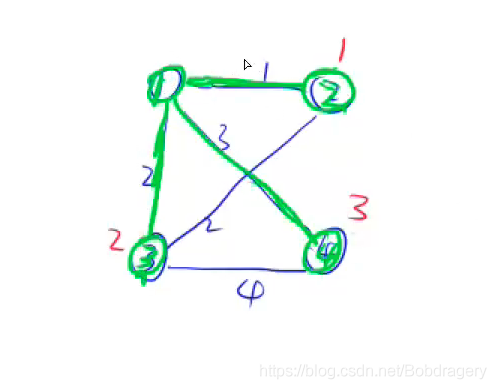
。
1、先初始化所有点距离为正无穷 。
2、迭代n次,依次用到集合的最小点更新剩余点距离 。
3、将已经确定的点加入到st集合中,st数组为一个bool类型 。
。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
|
/*
该图是稠密图,使用邻接矩阵
*/
package main
import (
"bufio"
"fmt"
"os"
"strconv"
"strings"
)
const (
N = 510
INF = 0x3f3f3f3f
)
var (
n, m int
dist [N]int
g [N][N]int
st [N]bool
)
func readLine(r *bufio.Reader) []int {
s, _ := r.ReadString('\n')
ss := strings.Fields(s)
res := make([]int, len(ss))
for i, v := range ss {
res[i], _ = strconv.Atoi(v)
}
return res
}
func prim() int {
// 初始化距离集合 dist
for i := 0; i < N; i++ {
dist[i] = 0x3f3f3f3f
}
// 迭代n次
res := 0 //res 存储最小生成树的大小即边的长度总和
for i := 0; i < n; i++ {
// 找到集合外距离最短的点
t := -1
for j := 1; j <= n; j++ {
if !st[j] && (t == -1 || dist[t] > dist[j]) {
t = j
}
}
// 迭代结束,此时的t就是距离最小点
// 情况一:图上的点不连通,不能组成最小生成树
if i > 0 && dist[t] == INF {
return INF
} // 如果不是第一个点并且最小店的距离是正无穷,则表示图是不连通的
if i > 0 {
res += dist[t]
} // 如果不是第一个点,这个t就表示当前点到集合某一个点的最小距离
// 用最小距离点更新其他跟 "现阶段形成的生成树" 的最短距离,
//注意更新的顺序,自环是不应该被加到最小生成树,所以,为了避免自环加入最小生成树,提前更新res
for j := 1; j <= n; j++ {
dist[j] = min(dist[j], g[t][j]) // 此步骤注意是dijkstra的区别,
}
st[t] = true
}
return res
}
func min(a, b int) int {
if a >= b {
return b
} else {
return a
}
}
func main() {
r := bufio.NewReader(os.Stdin)
input := readLine(r)
n, m = input[0], input[1]
//fmt.Scanf("%d%d\n", &n, &m)
// 初始化距离
for i := 0; i < N; i++ {
for j := 0; j < N; j++ {
if i == j {
g[i][j] = 0
} else {
g[i][j] = 0x3f3f3f3f
}
}
}
//
for m > 0 {
m--
in := readLine(r)
a, b, c := in[0], in[1], in[2] //输入
g[a][b] = min(g[a][b], c)
g[b][a] = g[a][b] // 无向图
}
t := prim()
if t == INF {
fmt.Println("impossible")
} else {
fmt.Println(t)
}
}
|
以上为个人经验,希望能给大家一个参考,也希望大家多多支持我。如有错误或未考虑完全的地方,望不吝赐教.
原文链接:https://blog.csdn.net/qq_23179075/article/details/102488447 。
最后此篇关于golang 实现菜单树的生成方式的文章就讲到这里了,如果你想了解更多关于golang 实现菜单树的生成方式的内容请搜索CFSDN的文章或继续浏览相关文章,希望大家以后支持我的博客! 。
背景: 我最近一直在使用 JPA,我为相当大的关系数据库项目生成持久层的轻松程度给我留下了深刻的印象。 我们公司使用大量非 SQL 数据库,特别是面向列的数据库。我对可能对这些数据库使用 JPA 有一
我已经在我的 maven pom 中添加了这些构建配置,因为我希望将 Apache Solr 依赖项与 Jar 捆绑在一起。否则我得到了 SolarServerException: ClassNotF
interface ITurtle { void Fight(); void EatPizza(); } interface ILeonardo : ITurtle {
我希望可用于 Java 的对象/关系映射 (ORM) 工具之一能够满足这些要求: 使用 JPA 或 native SQL 查询获取大量行并将其作为实体对象返回。 允许在行(实体)中进行迭代,并在对当前
好像没有,因为我有实现From for 的代码, 我可以转换 A到 B与 .into() , 但同样的事情不适用于 Vec .into()一个Vec . 要么我搞砸了阻止实现派生的事情,要么这不应该发
在 C# 中,如果 A 实现 IX 并且 B 继承自 A ,是否必然遵循 B 实现 IX?如果是,是因为 LSP 吗?之间有什么区别吗: 1. Interface IX; Class A : IX;
就目前而言,这个问题不适合我们的问答形式。我们希望答案得到事实、引用资料或专业知识的支持,但这个问题可能会引发辩论、争论、投票或扩展讨论。如果您觉得这个问题可以改进并可能重新打开,visit the
我正在阅读标准haskell库的(^)的实现代码: (^) :: (Num a, Integral b) => a -> b -> a x0 ^ y0 | y0 a -> b ->a expo x0
我将把国际象棋游戏表示为 C++ 结构。我认为,最好的选择是树结构(因为在每个深度我们都有几个可能的移动)。 这是一个好的方法吗? struct TreeElement{ SomeMoveType
我正在为用户名数据库实现字符串匹配算法。我的方法采用现有的用户名数据库和用户想要的新用户名,然后检查用户名是否已被占用。如果采用该方法,则该方法应该返回带有数据库中未采用的数字的用户名。 例子: “贾
我正在尝试实现 Breadth-first search algorithm , 为了找到两个顶点之间的最短距离。我开发了一个 Queue 对象来保存和检索对象,并且我有一个二维数组来保存两个给定顶点
我目前正在 ika 中开发我的 Python 游戏,它使用 python 2.5 我决定为 AI 使用 A* 寻路。然而,我发现它对我的需要来说太慢了(3-4 个敌人可能会落后于游戏,但我想供应 4-
我正在寻找 Kademlia 的开源实现C/C++ 中的分布式哈希表。它必须是轻量级和跨平台的(win/linux/mac)。 它必须能够将信息发布到 DHT 并检索它。 最佳答案 OpenDHT是
我在一本书中读到这一行:-“当我们要求 C++ 实现运行程序时,它会通过调用此函数来实现。” 而且我想知道“C++ 实现”是什么意思或具体是什么。帮忙!? 最佳答案 “C++ 实现”是指编译器加上链接
我正在尝试使用分支定界的 C++ 实现这个背包问题。此网站上有一个 Java 版本:Implementing branch and bound for knapsack 我试图让我的 C++ 版本打印
在很多情况下,我需要在 C# 中访问合适的哈希算法,从重写 GetHashCode 到对数据执行快速比较/查找。 我发现 FNV 哈希是一种非常简单/好/快速的哈希算法。但是,我从未见过 C# 实现的
目录 LRU缓存替换策略 核心思想 不适用场景 算法基本实现 算法优化
1. 绪论 在前面文章中提到 空间直角坐标系相互转换 ,测绘坐标转换时,一般涉及到的情况是:两个直角坐标系的小角度转换。这个就是我们经常在测绘数据处理中,WGS-84坐标系、54北京坐标系
在软件开发过程中,有时候我们需要定时地检查数据库中的数据,并在发现新增数据时触发一个动作。为了实现这个需求,我们在 .Net 7 下进行一次简单的演示. PeriodicTimer .
二分查找 二分查找算法,说白了就是在有序的数组里面给予一个存在数组里面的值key,然后将其先和数组中间的比较,如果key大于中间值,进行下一次mid后面的比较,直到找到相等的,就可以得到它的位置。

我是一名优秀的程序员,十分优秀!