个人中心
文章发布
退出
作者热门文章
- ubuntu12.04环境下使用kvm ioctl接口实现最简单的虚拟机
- Ubuntu 通过无线网络安装Ubuntu Server启动系统后连接无线网络的方法
- 在Ubuntu上搭建网桥的方法
- ubuntu 虚拟机上网方式及相关配置详解
24
4
CFSDN坚持开源创造价值，我们致力于搭建一个资源共享平台，让每一个IT人在这里找到属于你的精彩世界.
这篇CFSDN的博客文章Python多项式回归的实现方法由作者收集整理，如果你对这篇文章有兴趣，记得点赞哟.
多项式回归是一种线性回归形式，其中自变量x和因变量y之间的关系被建模为n次多项式。多项式回归拟合x的值与y的相应条件均值之间的非线性关系，表示为e（y | x） 。
为什么多项式回归:
多项式回归的使用:
这些基本上用于定义或描述非线性现象，例如:
回归分析的基本目标是根据自变量x的值来模拟因变量y的期望值。在简单回归中，我们使用以下等式 y = a + bx + e 。
这里y是因变量，a是y截距，b是斜率，e是误差率.
在许多情况下，这种线性模型将无法解决。例如，如果我们在这种情况下根据合成温度分析化学合成的产生，我们使用二次模型y = a + b1x + b2 ^ 2 + e 。
这里y是x的因变量，a是y截距，e是误差率.
通常，我们可以将其建模为第n个值。y = a + b1x + b2x ^ 2 + .... + bnx ^ n 。
由于回归函数在未知变量方面是线性的，因此这些模型从估计的角度来看是线性的.
因此，通过最小二乘技术，让我们计算y的响应值.
python中的多项式回归
要获得用于分析多项式回归的数据集，请单击此处.
步骤1：导入库和数据集 。
导入重要的库和我们用于执行多项式回归的数据集.
|
1
2
3
4
5
6
7
8
|
# importing the libraries
import
numpy as np
import
matplotlib.pyplot as plt
import
pandas as pd
# importing the dataset
datas
=
pd.read_csv(
'data.csv'
)
datas
|
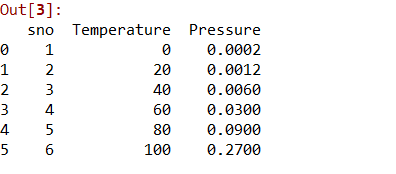
第2步：将数据集分为2个组件 。
将数据集划分为两个组件，即x和yx将包含1到2之间的列.y将包含2列.
|
1
2
|
x
=
datas.iloc[:,
1
:
2
].values
y
=
datas.iloc[:,
2
].values
|
第3步：将线性回归拟合到数据集 。
拟合线性回归模型在两个组件上.
|
1
2
3
4
5
|
# fitting linear regression to the dataset
from
sklearn.linear_model
import
linearregression
lin
=
linearregression()
lin.fit(x, y)
|
第4步：将多项式回归拟合到数据集 。
将多项式回归模型拟合到两个分量x和y上.
|
1
2
3
4
5
6
7
8
9
|
# fitting polynomial regression to the dataset
from
sklearn.preprocessing
import
polynomialfeatures
poly
=
polynomialfeatures(degree
=
4
)
x_poly
=
poly.fit_transform(x)
poly.fit(x_poly, y)
lin2
=
linearregression()
lin2.fit(x_poly, y)
|
步骤5：在此步骤中，我们使用散点图可视化线性回归结果.
|
1
2
3
4
5
6
7
8
9
|
# visualising the linear regression results
plt.scatter(x, y, color
=
'blue'
)
plt.plot(x, lin.predict(x), color
=
'red'
)
plt.title(
'linear regression'
)
plt.xlabel(
'temperature'
)
plt.ylabel(
'pressure'
)
plt.show()
|
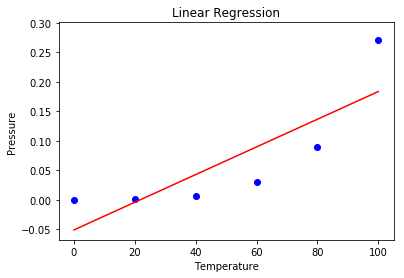
步骤6：使用散点图可视化多项式回归结果.
|
1
2
3
4
5
6
7
8
9
|
# visualising the polynomial regression results
plt.scatter(x, y, color
=
'blue'
)
plt.plot(x, lin2.predict(poly.fit_transform(x)), color
=
'red'
)
plt.title(
'polynomial regression'
)
plt.xlabel(
'temperature'
)
plt.ylabel(
'pressure'
)
plt.show()
|
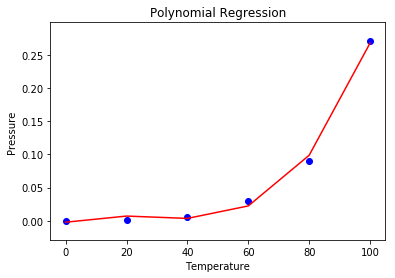
步骤7：使用线性和多项式回归预测新结果.
|
1
2
|
# predicting a new result with linear regression
lin.predict(
110.0
)
|
|
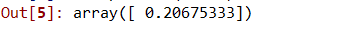
1
2
|
# predicting a new result with polynomial regression
lin2.predict(poly.fit_transform(
110.0
))
|
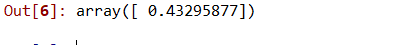
使用多项式回归的优点:
使用多项式回归的缺点 。
以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持我.
原文链接：https://www.cnblogs.com/python01/p/10329383.html 。
最后此篇关于Python多项式回归的实现方法的文章就讲到这里了,如果你想了解更多关于Python多项式回归的实现方法的内容请搜索CFSDN的文章或继续浏览相关文章，希望大家以后支持我的博客！ 。
24
4
0
所以我想创建一个程序，当用户输入值 c 且 a = 1 时，打印出可因式分解的二次方程。程序应确定 b 的所有可能的整数值，以便三项式以 x^2 + bx + c 的形式打印出来 一个例子是，如果用户
我有自己定义的多项式类，它是系数列表的形式。 有点像 axˆ2 + bx + c is equals to [c, b, a] (for ax + b == [b, a] similarly, for
我必须制作一个对多项式执行运算的 GUI，但我不断收到无法摆脱的 NullPointerExceptions。在输出上它没有显示任何内容。我尝试调试我的程序，据我所知，我从键盘插入的多项式在某种程度上
numpy.lib.polynomial.polyval 允许您使用另一个多项式评估多项式: numpy.polyval(poly1d([1, 2, 3]), 2) Out[832]: 11 nump
如果我想计算多项式，如何在 C 中定义具有可变数量参数的函数？我的函数必须有这个参数:第一个参数:float x，第二个:int n，其余的 float (系数)。非常感谢! 最佳答案 用 varia
我正在尝试求多项式的不定积分，但是我的数学和编码都不是很好。我的代码可以编译，但我相信我的公式有误: Polynomial Polynomial :: indefiniteIntegral() co
我有 3 个数据集。 2 表示多项式本身(我们称它们为 x 和 y)，1 表示函数值(它将是 z)。 多项式看起来像这样(假设两个维度的幂都是 3): z = a00 + a01*x + a02*x^
如何在 python 中计算最佳拟合线，然后将其绘制在 matplotlib 中的散点图上？ 我使用普通最小二乘回归计算线性最佳拟合线如下: from sklearn import linear_mo
我正在尝试分解 bool 多项式以获得逻辑网络的最小形式。我的变量是 a1、a2、a3 ... 以及负对应项 na1、na2、na3 ... 如果需要一个函数 f = a1*a2*b2*nb1 + a
长话短说 如何使用系数数组构建表达式并将其转换为 Func ？有没有比表达式树更好的方法？ 我有一个使用 Func formula 构造的不可变序列类型用于为序列 A 生成术语 An。我开始构建一个辅
我在我的 Mac OS Sierra 上运行 Spark 2.1.1(这应该有帮助)。我尝试在网上找到的测试数据集上拟合多项式逻辑回归，我在此处报告前几行(我不知道如何在此处附加文件): 1,0,24
我必须构建一个从类 lista(列表)继承的类多项式(polinom)。我必须从多项式类中加、减、乘、除 2 个对象。我有这段代码。我不明白为什么我的析构函数不工作。我还必须重载运算符:+、-、> 但
我有一个 Polynomial类，我正在尝试定义 operator++ ，递增前和递增后，以及尝试定义递减前和递减后，即 operator-- .这是我的代码片段: class Polynomial
我是编程新手(Python 是我的第一语言)，但我喜欢设计算法。我目前正在研究方程组(整数)，但找不到任何解决我的特定问题的引用。 让我解释一下。 我有一个等式(一个测试，如果你愿意的话): raw_
我正在尝试使用 scipy.stats (python) 中的 multinominal.pmf 函数。 当我在输入中所有概率都大于零的情况下使用此函数时，它工作正常。问题是当我想在其中一个概率为零时
我想用 0xA001 多项式计算字节数组的 CRC-16 校验和。但我真的不知道如何在 Java 中做到这一点，以及如何使用给定的多项式。它是某种特殊值(0xA001)吗？你能告诉我一个可以为我计算校
由于我的分类器在测试数据上产生了大约 99% 的准确率，我有点怀疑并想深入了解我的 NB 分类器最有用的特征，看看它正在学习什么样的特征。以下主题非常有用:How to get most inform
如 McFadden (1978)表明，如果多项 logit 模型中的备选方案数量大到无法计算，则通过对备选方案进行随机子集来获得一致估计仍然是可行的，因此每个个体的估计概率基于所选备选方案和 C其他
我现在有一些离散点，我使用 scipy.interpolate.splprep () 函数(B 样条插值)对其进行插值，以获得令人满意的平滑曲线。这是代码(借鉴另一个问题的答案)和我得到的结果。 im
我在 IPython notebook 中有一些多项式 x: import numpy as np x = np.polynomial.polynomial.Polynomial([1,2,3]) x
我是一名优秀的程序员,十分优秀！