CFSDN坚持开源创造价值，我们致力于搭建一个资源共享平台，让每一个IT人在这里找到属于你的精彩世界.

这篇CFSDN的博客文章Python 内部是如何实现整数相加不溢出的？由作者收集整理，如果你对这篇文章有兴趣，记得点赞哟.

 1、如何表示一个整数

要想了解这个，那就需要看 Python 的源代码[1]，Python中的整数底层对应的结构体是PyLongObject，它位于 longobject.h[2] 中.

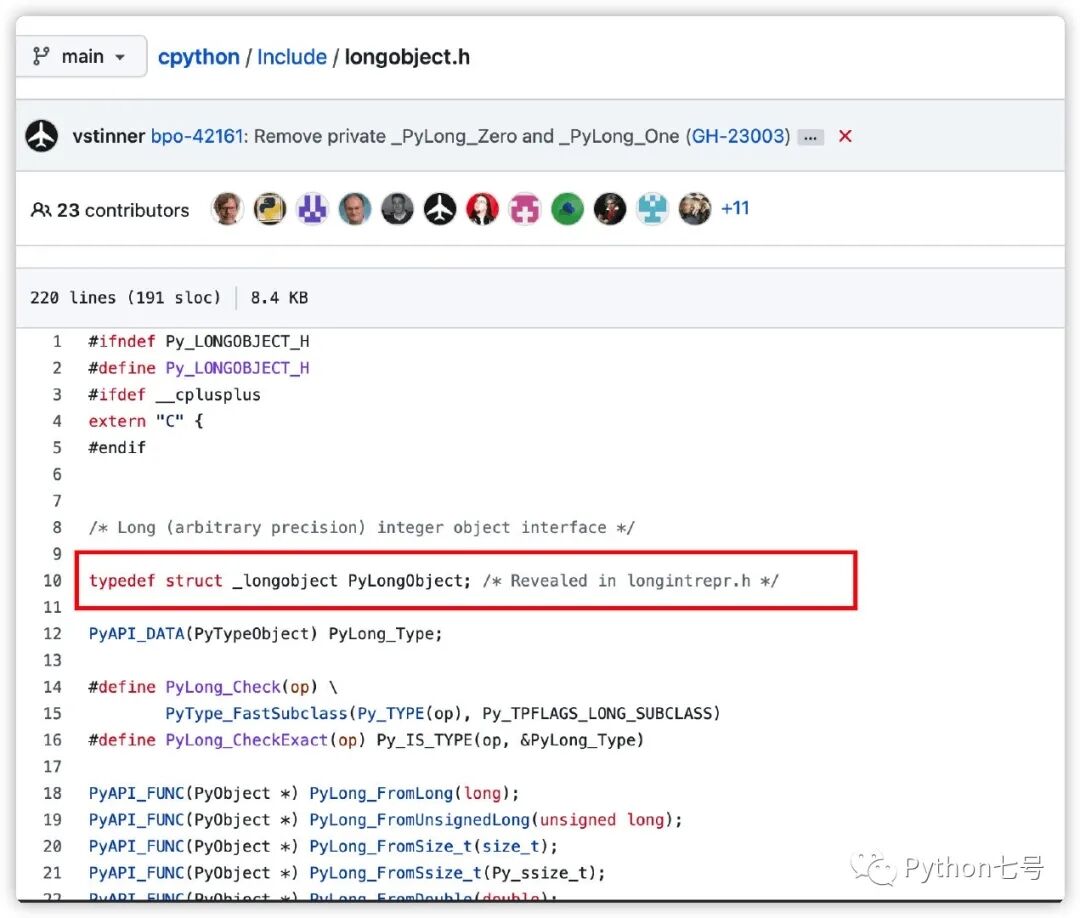
逐步展开如下:

1. //longobject.h 
2. typedef struct _longobject PyLongObject; /* Revealed in longintrepr.h */ 
3.   
4. //longintrepr.h 
5. struct _longobject { 
6.     PyObject_VAR_HEAD 
7.     digit ob_digit[1]; 
8. }; 
9.   
10. //合起来可以看成 
11. typedef struct { 
12.     PyObject_VAR_HEAD 
13.     digit ob_digit[1]; 
14. } PyLongObject; 

再把宏定义 PyObject_VAR_HEAD 展开:

1. typedef struct { 
2.     PyObject_HEAD 
3.     int ob_size; 
4.     digit ob_digit[1]; 
5. } PyLongObject; 

再把宏定义 PyObject_HEAD 展开，结构体中的变量我已经作了注释:

1. typedef struct { 
2.     int ob_refcnt;    //引用计数 
3.     struct _typeobject *ob_type; //变量类型 
4.     int ob_size;       //用来指明变长对象中一共容纳了多少个元素 
5.     digit ob_digit[1]; //digit类型的数组,长度为1 
6. } PyLongObject; 

这里面的 ob_size 用来指明变长对象中一共容纳了多少个元素，也就是 ob_digit 数组的长度，而这个 ob_digit 数组显然只能是用来维护具体的值.

到这里已经很明显了，Python 将大整数切割后存在 ob_digit，这个数组的长度是可变的，数据越大，数组越长，只要内存够用，存多大的数都可以.

那么下面的重点就在这个 ob_digit 数组了，我们看看 Python 中整数对应的值，比如 256，是怎么放在这个数组里面的。不过首先我们要看看这个digit 是个什么类型，它同样定义在 longintrepr.h 中 。

1. #if PYLONG_BITS_IN_DIGIT == 30 
2. typedef uint32_t digit; 
3. // ... 
4. #elif PYLONG_BITS_IN_DIGIT == 15 
5. typedef unsigned short digit; 
6. // ... 
7. #endif 

PYLONG_BITS_IN_DIGIT 是一个宏，如果你的机器是 64 位的，那么它会被定义为 30，32 位机器则会被定义为 15.

而我们的机器现在基本上都是 64 位的，所以 PYLONG_BITS_IN_DIGIT会等于 30，因为 digit 等价于 uint32_t(unsigned int)，所以它是一个无符号 32 位整型.

所以 ob_digit 这个数组是一个无符号 32 位整型数组，长度为 1。当然这个数组具体多长则取决于你要存储的 Python 整数有多大，因为 C 中数组的长度不属于类型信息，你可以看成是长度 n，而这个 n 是多少要取决于你的整数大小。显然整数越大，这个数组就越长，那么占用空间就越大.

为了说明 256 是如何存放在 ob_digit 里的，我们来简化下，这里假如 ob_digit 这个数组是一个无符号 8 位整型数组，8 位二进制，最大只能表示 255，我们要表示 256，那就只能再申请一个 8 位，也许你认为再申请一个 8 位来表示 1，其实不是的，是使用一个新的 8 位整数来模拟更高的位，如下所示:

1. 255 = [255] 
2. 256 = [1,1] 

256 = [1,1] 的形式也不是真实情况，为了你理解，先这样写，它表达的意思就是 256 = 1 + 1 * (2^8 - 1) = 1 + 1 * 255 = 256.

也就是说 ob_digit 表示 x 进制数，ob_digit[0] 是低位，ob_digit[1] 是高位，具体 x 是多少，取决于 ob_digit 的类型，这里 8 位，就是 255 进制.

刚才提到 256 = [1,1] 的形式也不是真实情况，因为 PyLongObject 不仅仅是为了存储大整数，也需要参与运算，具体怎么运算呢，那就是 ob_digit 逐位相加即可.

既然是相加，即又可能溢出，比如 [255 , 1] + [255, 1] = [510,2] 。

这里的 510 就超出了 8 位，为了简化处理，只要我们不用满 8 位，就不会溢出，也就是说，比如说只用 7 位，那最大也就是 [127,...] + [127,...] = [254,...] 也就不会溢出了.

到这里，你会明白，为什么 digit 虽然是无符号 32 位整数，却只使用 30 位了吧:

1. #if PYLONG_BITS_IN_DIGIT == 30 
2. typedef uint32_t digit; 
3. // ... 
4. #elif PYLONG_BITS_IN_DIGIT == 15 
5. typedef unsigned short digit; 
6. // ... 
7. #endif 

聪明的你，可能会问，31 位就可以保证不溢出，为啥牺牲两位，用 30 位，答案我也不知道，可能是因为 64 是 32 的两倍， 30 也是 15 的两倍，这样看起来更舒服吧.

那如何表示负数呢，其实负数的话，就是 ob_size 变成了负的，其他没变。整数的正负号是通过这里的 ob_size 决定的。ob_digit 存储的其实是绝对值，无论 n 取多少，-n 和 n 对应的 ob_digit 是完全一致的，但是ob_size 则互为相反数。所以 ob_size 除了表示数组的长度之外，还可以表示对应整数的正负.

所以 Python 在比较两个整型的大小时，会先比较 ob_size，如果 ob_size 不一样则可以直接比较出大小来.

总结一下，就是当 PYLONG_BITS_IN_DIGIT == 30 的时候，整数 = ob_digit[0] + ob_digit[1] * 2 ** 30 + ob_digit[2] * 2 ** 60 + ... 。

2、整数占用内存大小

理解了这一点，我们再看一下这个结构体:

1. typedef struct { 
2.     int ob_refcnt;    //引用计数 
3.     struct _typeobject *ob_type; //变量类型 
4.     int ob_size;       //用来指明变长对象中一共容纳了多少个元素 
5.     digit ob_digit[1]; //digit类型的数组,长度为1 
6. } PyLongObject; 

一个整数占用多少个字节，取决于 PyLongObject 这个结构体占用多少字节，ob_refcnt、ob_type、ob_size 这三个是整数所必备的，它们都是 8 字节，加起来 24 字节。所以任何一个整数所占内存都至少 24 字节，至于具体占多少，则取决于 ob_digit 里面的元素都多少个.

现在的你不难理解以下结果:

3、整数池

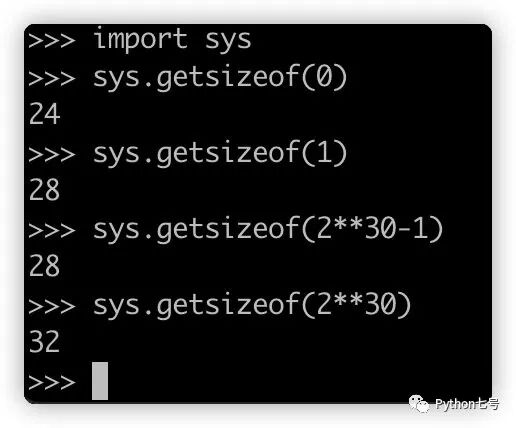
此外 Python 中的整数属于不可变对象，运算之后会创建新的对象

1. >>> a = 300 
2. >>> id(a) 
3. 140220663619152 
4. >>> a += 1 
5. >>> id(a) 
6. 140220663619408 
7. >>> 

这样就势必会有性能缺陷，因为程序运行时会有对象的创建和销毁，就是涉及内存的申请和垃圾回收，一个常用的手段就是使用对象池，将频率高的整数预先创建好，而且都是单例模式，需要使用时直接返回.

小整数对象池的实现位于 pycore_interp.h[3] 中:

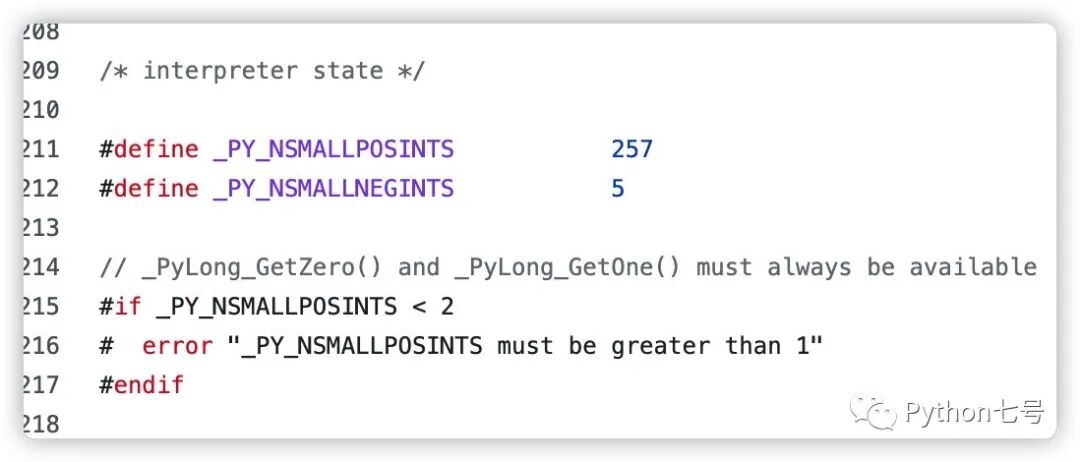
验证一下:

1. >>> a = -6 
2. >>> b = -6 
3. >>> a is b 
4. False 
5. >>> a = -5 
6. >>> b = -5 
7. >>> a is b 
8. True 
9. >>> a = 256 
10. >>> b = 256 
11. >>> a is b 
12. True 
13. >>> a = 257 
14. >>> b = 257 
15. >>> a is b 
16. False 
17. >>> 

不同的版本可能会不同，我这里 Python3.8，区间为 [-5,257).

4、整数加减法

有了前面的铺垫，现在我们来看下 Python 中大整数是如何相加的，源代码 longobject.c : long_add 函数[4] 。

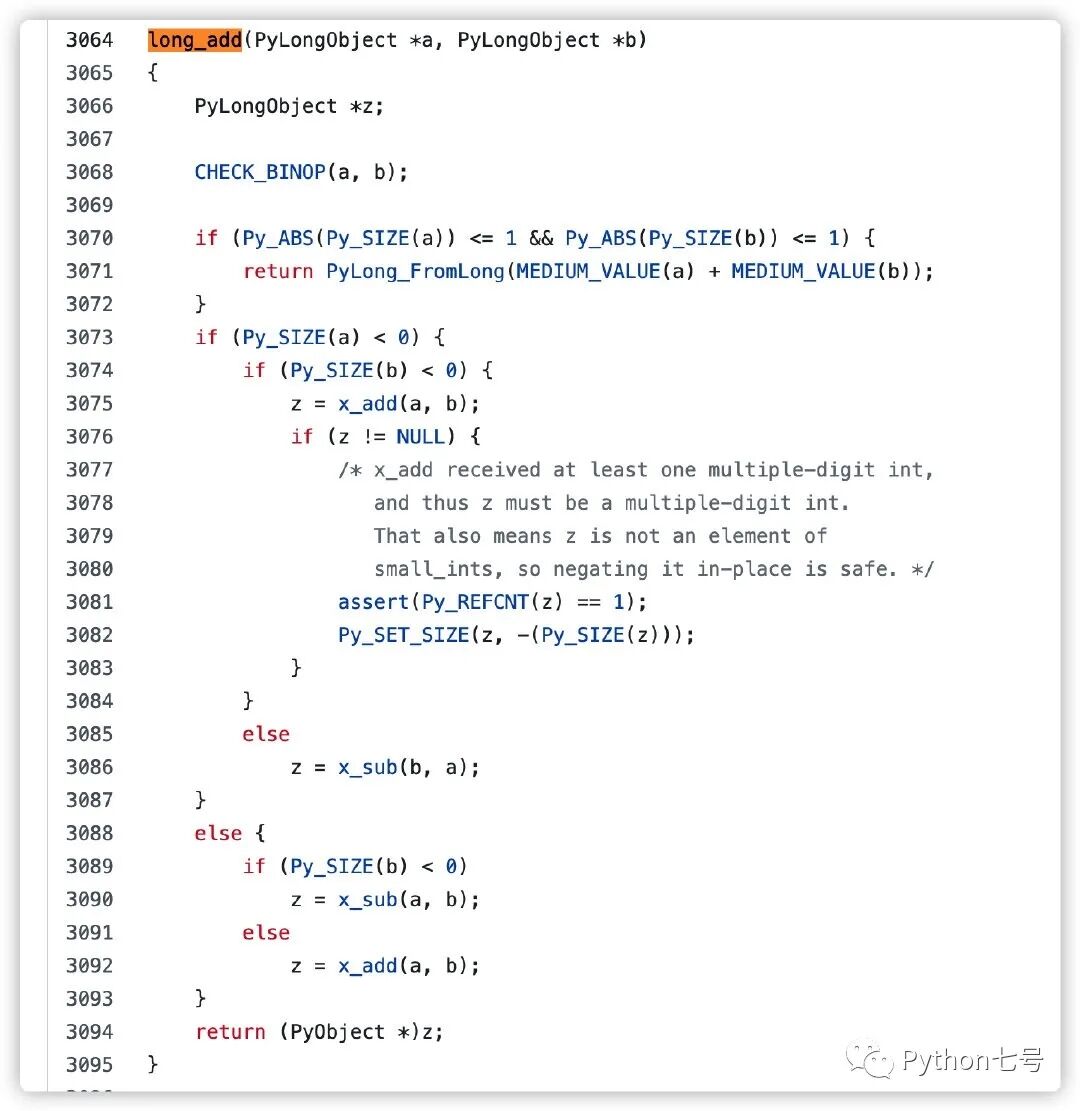
可以看到 long_add 根据 ob_size 的正或负来调用 x_add 或 x_sub.

现在看一下 x_add 的源代码:

可以看到，Python 大整数的相加就是底层数组的相加，当然还会涉及到进位等操作:

1. for (i = 0; i < size_b; ++i) { 
2.  carry += a->ob_digit[i] + b->ob_digit[i]; 
3.  z->ob_digit[i] = carry & PyLong_MASK; 
4.  carry >>= PyLong_SHIFT; 
5. } 

x_sub 的源代码:

4、整数乘法

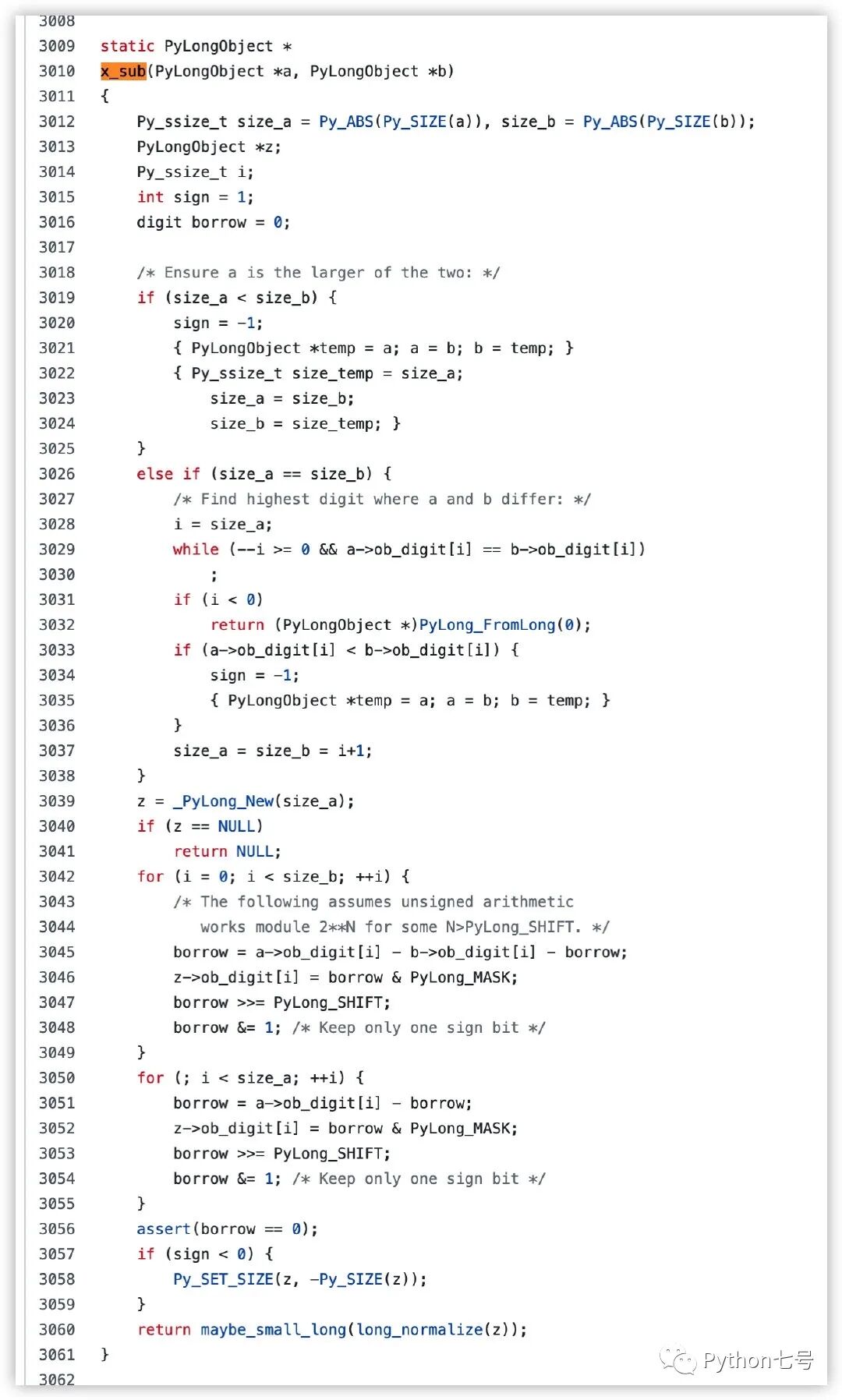
Python 整数乘法使用的是 Karatsuba multiplication[5] 算法进行的大数乘法，感兴趣的可以研究一下.

最后的话

源码之下无秘密，看源码会比较辛苦，却可以学到精髓和本质，本文通过源码逐层展开，带你了解了下 Python 整数对象的实现、整数内存大小的计算，整数池，整数加减法源码，相信你已经知道了 Python 是如何实现整数想加而不溢出的。如果有收获，还请点在、点赞、转发，感谢一路的支持和陪伴.

原文链接：https://mp.weixin.qq.com/s?__biz=MzU0OTg3NzU2NA==&mid=2247487960&idx=1&sn=9be99d54fb47fdd2f6fc6f8b9c37e3f7&chksm=fba8738bccdffa9dafbcc0055c0079fe1b1a50622d0607fee183fc00d1a68abb99e1db4e943f&mpshare=1& 。

最后此篇关于Python 内部是如何实现整数相加不溢出的？的文章就讲到这里了,如果你想了解更多关于Python 内部是如何实现整数相加不溢出的？的内容请搜索CFSDN的文章或继续浏览相关文章，希望大家以后支持我的博客！ 。