CFSDN坚持开源创造价值，我们致力于搭建一个资源共享平台，让每一个IT人在这里找到属于你的精彩世界.

这篇CFSDN的博客文章详解C++实现匈牙利算法由作者收集整理，如果你对这篇文章有兴趣，记得点赞哟.

1、匈牙利算法介绍

匈牙利算法（hungarian algorithm）主要用于解决一些与二分图匹配有关的问题，所以我们先来了解一下二分图.

二分图（bipartite graph）是一类特殊的图，它可以被划分为两个部分，每个部分内的点互不相连。下图是典型的二分图.

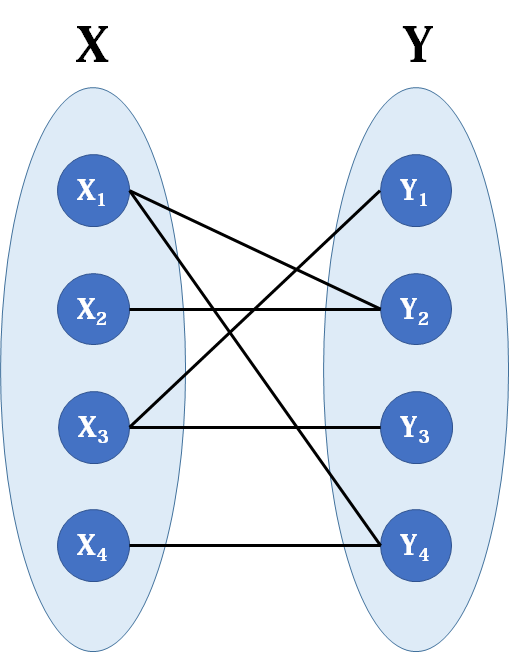
可以看到，在上面的二分图中，每条边的端点都分别处于点集x和y中。匈牙利算法主要用来解决两个问题：求二分图的最大匹配数和最小点覆盖数.

这么说起来过于抽象了，我们现在从实际问题出发.

2、最大匹配问题

看完上面讲的，相信读者会觉得云里雾里的：这是啥？这有啥用？所以我们把这张二分图稍微做点手脚，变成下面这样:

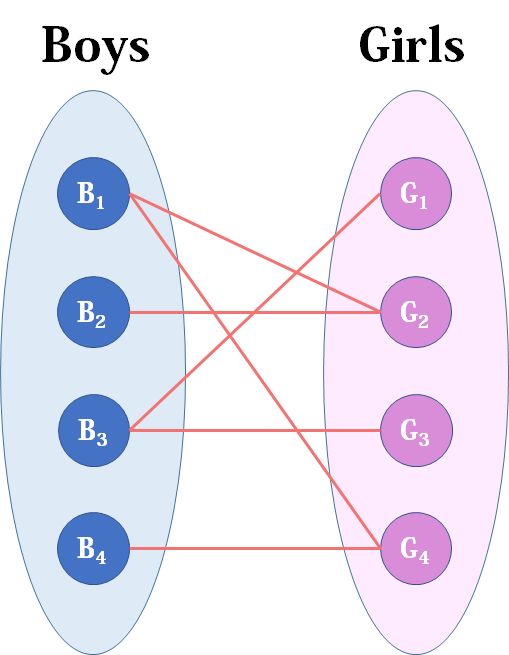
现在boys和girls分别是两个点集，里面的点分别是男生和女生，边表示他们之间存在“暧昧关系"。最大匹配问题相当于，假如你是红娘，可以撮合任何一对有暧昧关系的男女，那么你最多能成全多少对情侣？（数学表述：在二分图中最多能找到多少条没有公共端点的边） 。

现在我们来看看匈牙利算法是怎么运作的:

我们从b1看起（男女平等，从女生这边看起也是可以的），他与g2有暧昧，那我们就先暂时把他与g2连接（注意这时只是你作为一个红娘在纸上构想，你没有真正行动，此时的安排都是暂时的）.

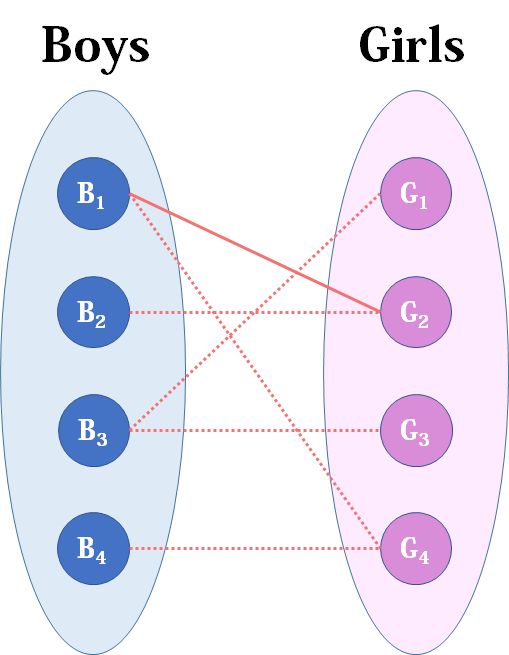
来看b2，b2也喜欢g2，这时g2已经“名花有主”了（虽然只是我们设想的），那怎么办呢？我们倒回去看g2目前被安排的男友，是b1，b1有没有别的选项呢？有，g4，g4还没有被安排，那我们就给b1安排上g4.

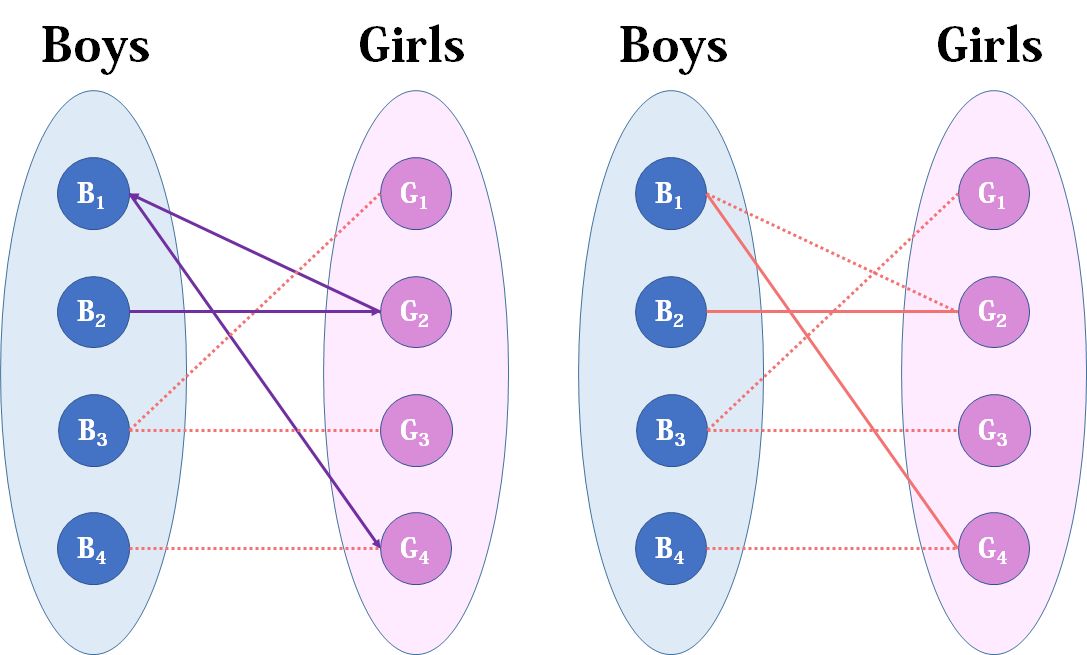
然后b3，b3直接配上g1就好了，这没什么问题。至于b4，他只钟情于g4，g4目前配的是b1。b1除了g4还可以选g2，但是呢，如果b1选了g2，g2的原配b2就没得选了。我们绕了一大圈，发现b4只能注定单身了，可怜。（其实从来没被考虑过的g3更可怜） 。

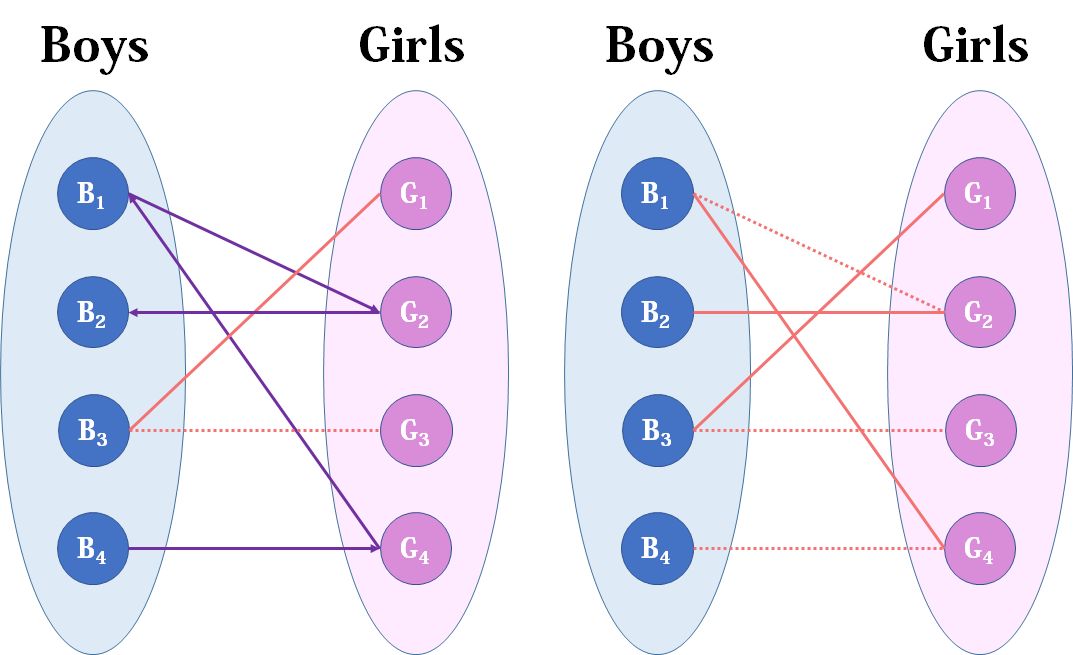
这就是匈牙利算法的流程，至于具体实现，我们来看看代码:

其实流程跟我们上面描述的是一致的。注意这里使用了一个递归的技巧，我们不断往下递归，尝试寻找合适的匹配.

3、最小点覆盖问题

另外一个关于二分图的问题是求最小点覆盖：我们想找到最少的一些点，使二分图所有的边都至少有一个端点在这些点之中。倒过来说就是，删除包含这些点的边，可以删掉所有边.

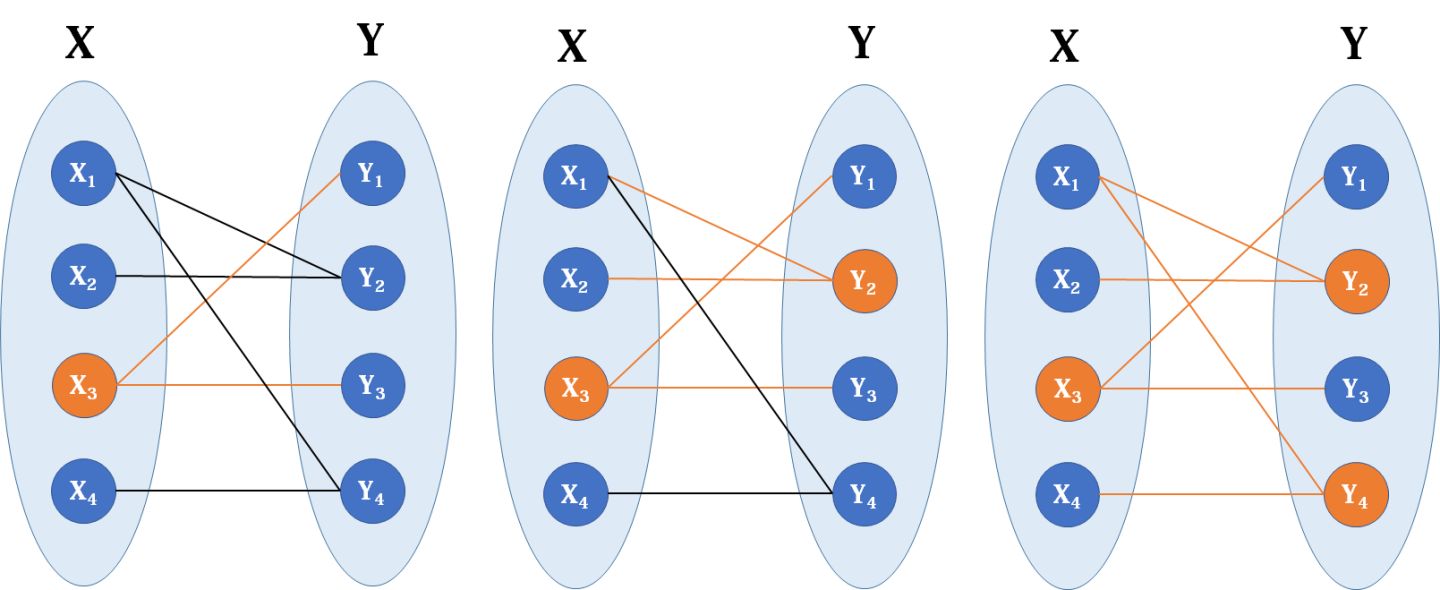
这为什么用匈牙利算法可以解决呢？你如果以为我要长篇大论很久就错了，我们只需要一个定理:

（könig定理） 。

一个二分图中的最大匹配数等于这个图中的最小点覆盖数.

好了，本节可以结束了，我们不是搞数学的，不需要证明。但是提供一个直观地找最小覆盖点集的方法：看题图，从左侧一个未匹配成功的点出发，走一趟匈牙利算法的流程（即紫色的箭头），所有左侧未经过的点，和右侧经过的点，即组成最小点覆盖。（即图中的b3、g2、g4） 。

对于每个左部节点，寻找增广路最多遍历整张二分图一次，因此，该算法时间复杂度为o(mn) 。

4、匈牙利算法的应用

一些题目，乍一看与上面这个男女配对的问题没有任何相似点，其实都可以用匈牙利算法。例如:

4.1、（洛谷p1129） [zjoi2007]矩阵游戏

题目描述 。

小q是一个非常聪明的孩子，除了国际象棋，他还很喜欢玩一个电脑益智游戏――矩阵游戏。矩阵游戏在一个$ n× n $ 黑白方阵进行（如同国际象棋一般，只是颜色是随意的）。每次可以对该矩阵进行两种操作： 行交换操作：选择矩阵的任意两行，交换这两行（即交换对应格子的颜色） 列交换操作：选择矩阵的任意两列，交换这两列（即交换对应格子的颜色） 游戏的目标，即通过若干次操作，使得方阵的主对角线(左上角到右下角的连线)上的格子均为黑色。 对于某些关卡，小q百思不得其解，以致他开始怀疑这些关卡是不是根本就是无解的！于是小q决定写一个程序来判断这些关卡是否有解。 输入格式 第一行包含一个整数t，表示数据的组数。 接下来包含t组数据，每组数据第一行为一个整数n，表示方阵的大小；接下来n行为一个 $ n× n $的01矩阵（0表示白色，1表示黑色）。 输出格式 包含t行。对于每一组数据，如果该关卡有解，输出一行yes；否则输出一行no.

我们把矩阵转化为二分图（左侧集合代表各行，右侧集合代表各列，某位置为1则该行和该列之间有边）。我们想进行一系列交换操作，使得x1连上y1，x2连上y2，…… 。

大家可以想象，所谓的交换，是不是可以等价为重命名？我们可以在保持当前二分图结构不变的情况下，把右侧点的编号进行改变，这与交换的效果是一样的.

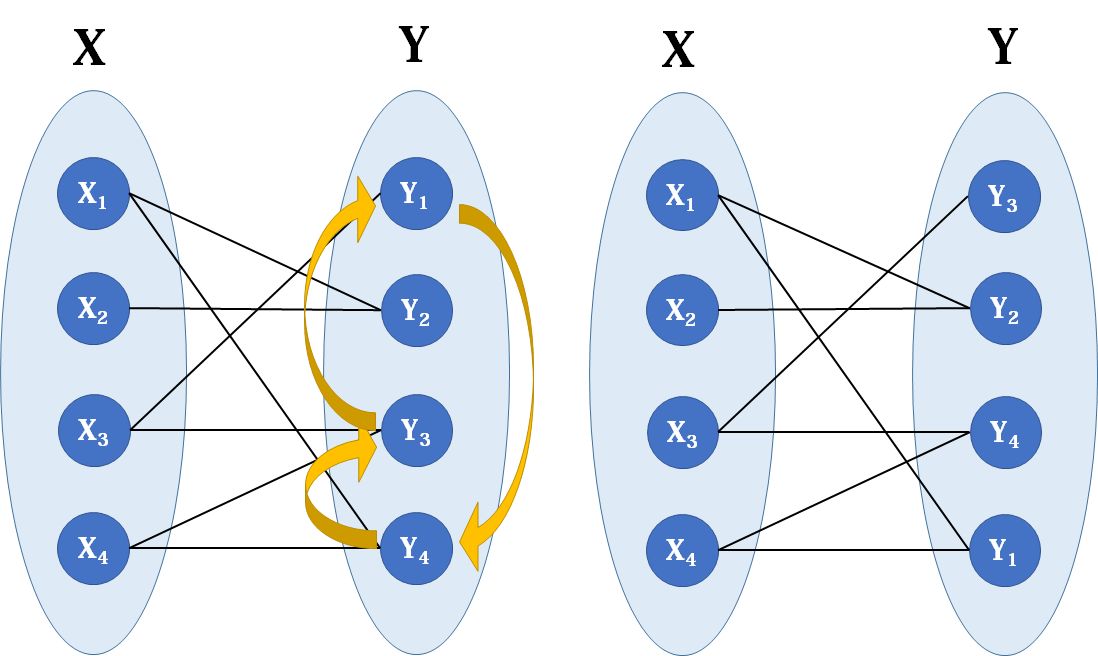
所以想让x1、x2...与y1、y2...一一对应，其实只需要原图最大匹配数为4就行了。（这与组合数学中相异代表系的概念相合）。代码如下:

4.2、（vijos1204） covh之柯南开锁

面对oibh组织的嚣张气焰, 柯南决定深入牛棚, 一探虚实. 他经过深思熟虑, 决定从oibh组织大门进入........... oibh组织的大门有一个很神奇的锁. 锁是由m*n个格子组成, 其中某些格子凸起(灰色的格子). 每一次操作可以把某一行或某一列的格子给按下去. 。

如果柯南能在组织限定的次数内将所有格子都按下去, 那么他就能够进入总部. 但是oibh组织不是吃素的, 他们的限定次数恰是最少次数. 。

请您帮助柯南计算出开给定的锁所需的最少次数. 。

读入/input:

第一行 两个不超过100的正整数n, m表示矩阵的长和宽 以下n行 每行m个数 非0即1 1为凸起方格 。

输出/output:

一个整数 所需最少次数 。

如果我们把样例的矩阵，转化为二分图的形式，是这样的:

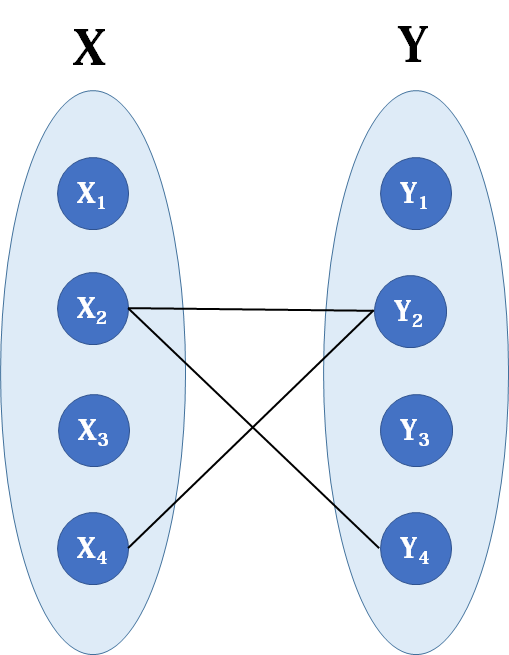
按下一行或一列，其实就是删掉与某个点相连的所有边。现在要求最少的操作次数，想想看，这不就是求最小点覆盖数吗？所以直接套匈牙利算法即可。代码略.

4.3、（tyvj p1035） 棋盘覆盖

描述 description 给出一张nn(n<=100)的国际象棋棋盘，其中被删除了一些点，问可以使用多少12的多米诺骨牌进行掩盖。 输入格式 input format 第一行为n，m（表示有m个删除的格子） 第二行到m+1行为x,y，分别表示删除格子所在的位置 x为第x行 y为第y列 输出格式 output format 一个数，即最大覆盖格数 。

经典的多米诺覆盖问题大家都很熟悉，我们把棋盘染色，每个多米诺骨牌恰好覆盖一个白格和一个黑格（这里为了美观染成了其他颜色，下面仍将其称作黑格）.

我们删除了一些格子:

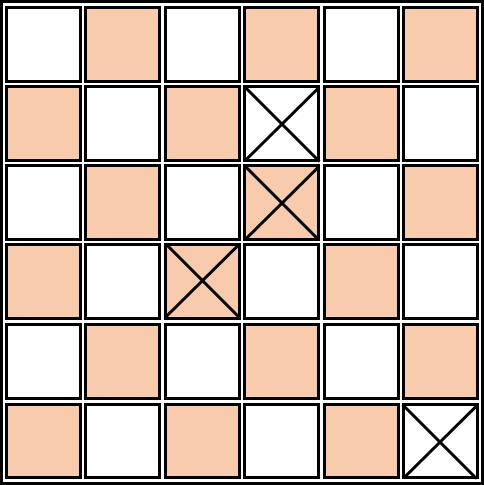
现在要求多米诺骨牌最大覆盖数.

你可能已经看出来了，我们在染色之后，黑格和白格可以构成一个二分图，每个白格都只和黑格相连，每个黑格也只和白格相连。在给所有黑格和白格编号后，我们把每个未删除的格子都与它上下左右紧邻的未删除的格子相连。很显然，这张二分图的最大匹配数，就是我们能放下最多的多米诺骨牌数。注意因为数据范围较大，要用邻接表存图.

以上就是详解c++实现匈牙利算法的详细内容，更多关于c++匈牙利算法的资料请关注我其它相关文章！ 。

原文链接：https://www.cnblogs.com/RioTian/p/13473634.html 。

最后此篇关于详解C++实现匈牙利算法的文章就讲到这里了,如果你想了解更多关于详解C++实现匈牙利算法的内容请搜索CFSDN的文章或继续浏览相关文章，希望大家以后支持我的博客！ 。