- ubuntu12.04环境下使用kvm ioctl接口实现最简单的虚拟机
- Ubuntu 通过无线网络安装Ubuntu Server启动系统后连接无线网络的方法
- 在Ubuntu上搭建网桥的方法
- ubuntu 虚拟机上网方式及相关配置详解
CFSDN坚持开源创造价值,我们致力于搭建一个资源共享平台,让每一个IT人在这里找到属于你的精彩世界.
这篇CFSDN的博客文章python scipy 稀疏矩阵的使用说明由作者收集整理,如果你对这篇文章有兴趣,记得点赞哟.
是最简单的稀疏矩阵存储方式,采用三元组(row, col, data)(或称为ijv format)的形式来存储矩阵中非零元素的信息.
在实际使用中,一般coo_matrix用来创建矩阵,因为coo_matrix无法对矩阵的元素进行增删改操作;创建成功之后可以转化成其他格式的稀疏矩阵(如csr_matrix、csc_matrix)进行转置、矩阵乘法等操作.
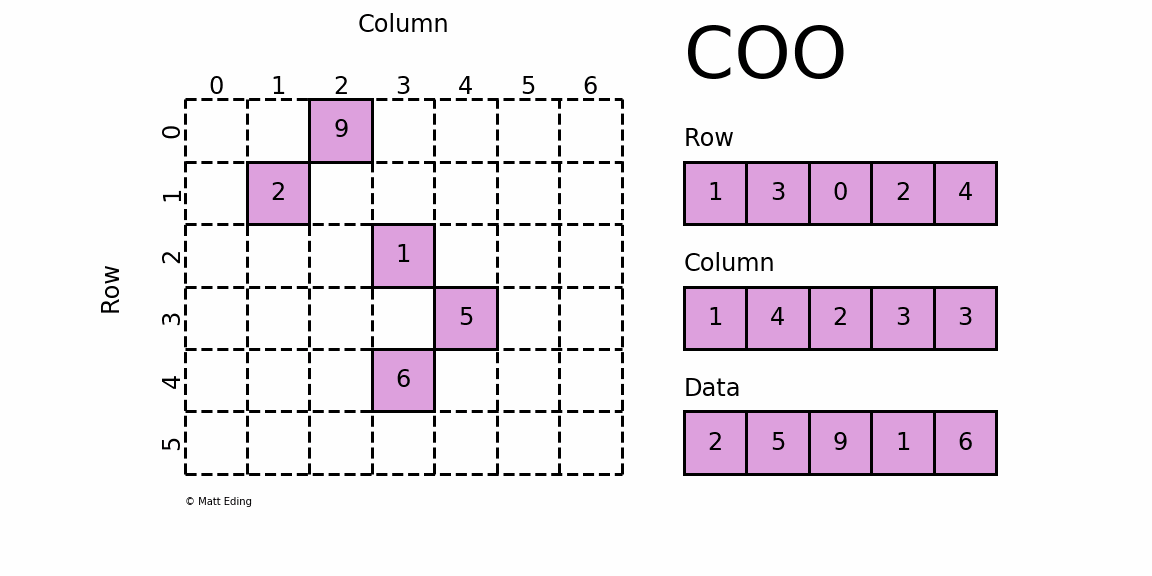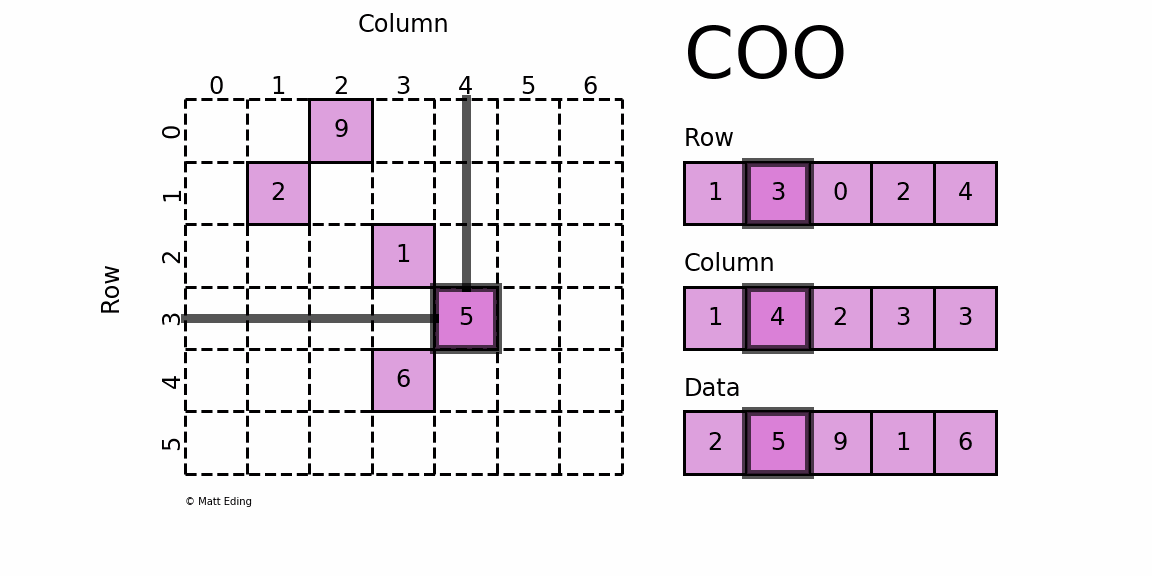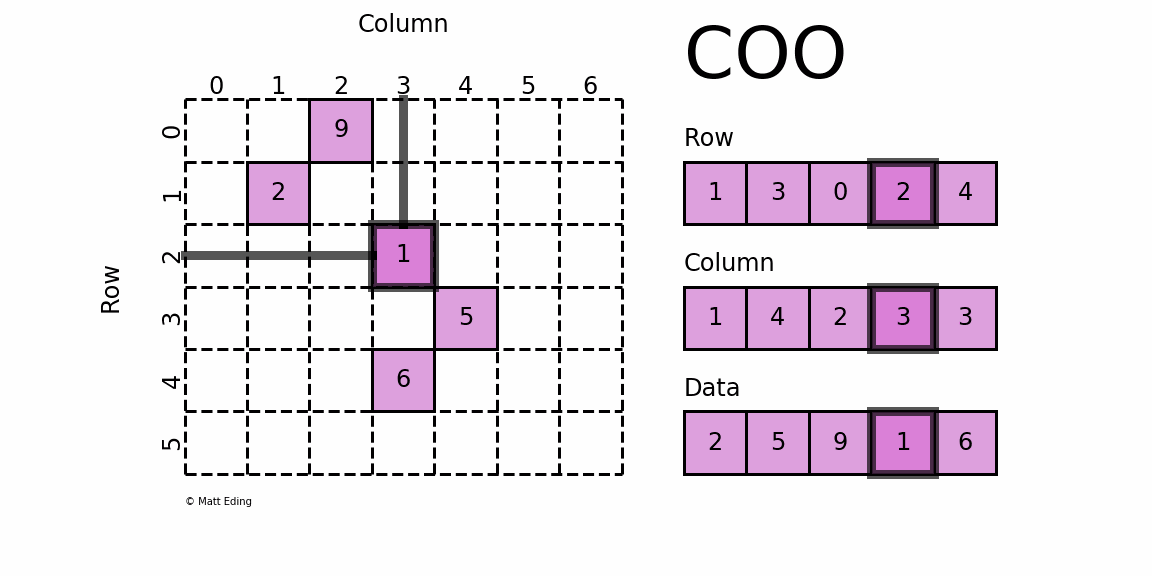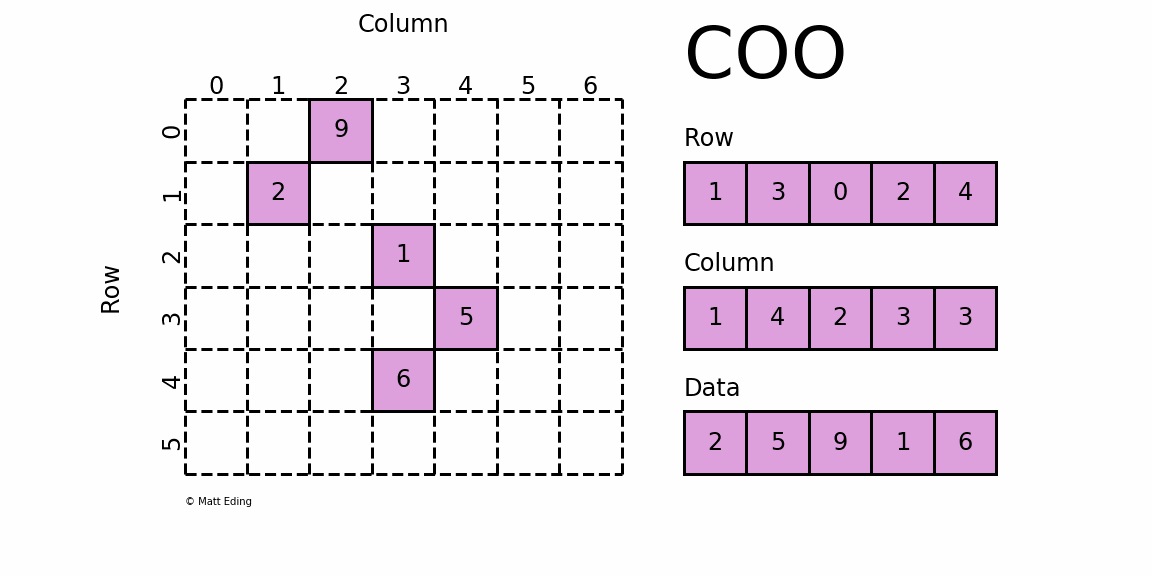
coo_matrix可以通过四种方式实例化,除了可以通过coo_matrix(D), D代表密集矩阵;coo_matrix(S), S代表其他类型稀疏矩阵或者coo_matrix((M, N), [dtype])构建一个shape为M*N的空矩阵,默认数据类型是d,还可以通过(row, col, data)三元组初始化:
>>> import numpy as np>>> from scipy.sparse import coo_matrix>>> _row = np.array([0, 3, 1, 0])>>> _col = np.array([0, 3, 1, 2])>>> _data = np.array([4, 5, 7, 9])>>> coo = coo_matrix((_data, (_row, _col)), shape=(4, 4), dtype=np.int)>>> coo.todense() # 通过toarray方法转化成密集矩阵(numpy.matrix)>>> coo.toarray() # 通过toarray方法转化成密集矩阵(numpy.ndarray)array([[4, 0, 9, 0], [0, 7, 0, 0], [0, 0, 0, 0], [0, 0, 0, 5]])
上面通过triplet format的形式构建了一个coo_matrix对象,我们可以看到坐标点(0,0)对应值为4,坐标点(1,1)对应值为7等等,这就是coo_matrix。coo_matrix对象有很多方法,大多数是elementwise的操作函数;coo_matrix对象有以下属性:
dtype dtype 。
矩阵中元素的数据类型 。
shape 2-tuple 。
获取矩阵的shape 。
ndim int 。
获取矩阵的维度,当然值是2咯 。
nnz 。
存储值的个数,包括显示声明的零元素(注意) 。
data 。
稀疏矩阵存储的值,是一个一维数组,即上面例子中的_data 。
row 。
与data同等长度的一维数组,表征data中每个元素的行号 。
col 。
与data同等长度的一维数组,表征data中每个元素的列号 。
在实际应用中,coo_matrix矩阵文件通常存成以下形式,表示稀疏矩阵是coo_matrix(coordinate),由13885行1列组成,共有949个元素值为非零,数据类型为整形.
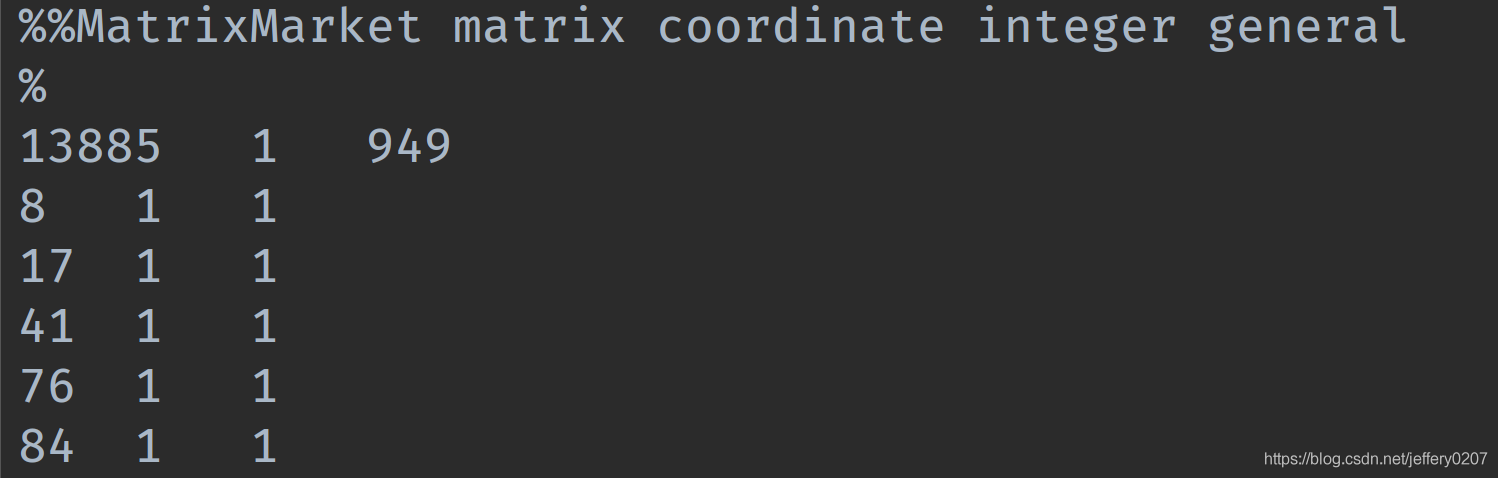
下面给出coo_matrix矩阵文件读写示例代码,mmread()用于读取稀疏矩阵,mmwrite()用于写入稀疏矩阵,mminfo()用于查看稀疏矩阵文件元信息。(这三个函数的操作不仅仅限于coo_matrix) 。
from scipy.io import mmread, mmwrite, mminfoHERE = dirname(__file__)coo_mtx_path = join(HERE, "data/matrix.mtx")coo_mtx = mmread(coo_mtx_path)print(mminfo(coo_mtx_path))# (13885, 1, 949, "coordinate", "integer", "general")# (rows, cols, entries, format, field, symmetry)mmwrite(join(HERE, "data/saved_mtx.mtx"), coo_mtx)
coo_matrix的优点:
有利于稀疏格式之间的快速转换(tobsr()、tocsr()、to_csc()、to_dia()、to_dok()、to_lil()) 。
允许又重复项(格式转换的时候自动相加) 。
能与CSR / CSC格式的快速转换 。
coo_matrix的缺点:
不能直接进行算术运算 。
csr_matrix,全称Compressed Sparse Row matrix,即按行压缩的稀疏矩阵存储方式,由三个一维数组indptr, indices, data组成.
这种格式要求矩阵元按行顺序存储,每一行中的元素可以乱序存储.
那么对于每一行就只需要用一个指针表示该行元素的起始位置即可.
indptr存储每一行数据元素的起始位置,indices这是存储每行中数据的列号,与data中的元素一一对应.
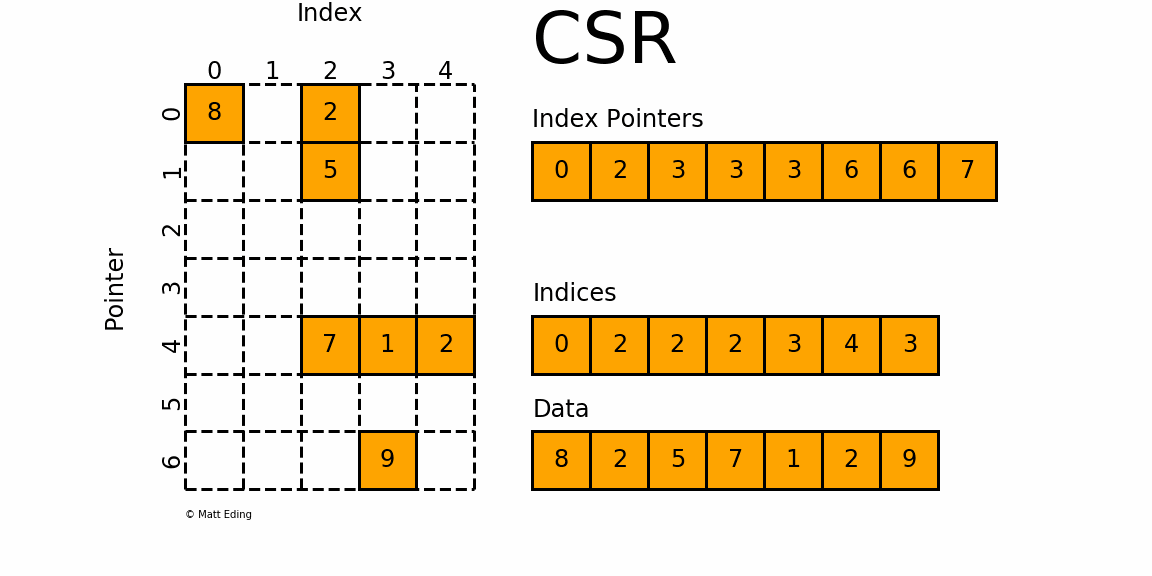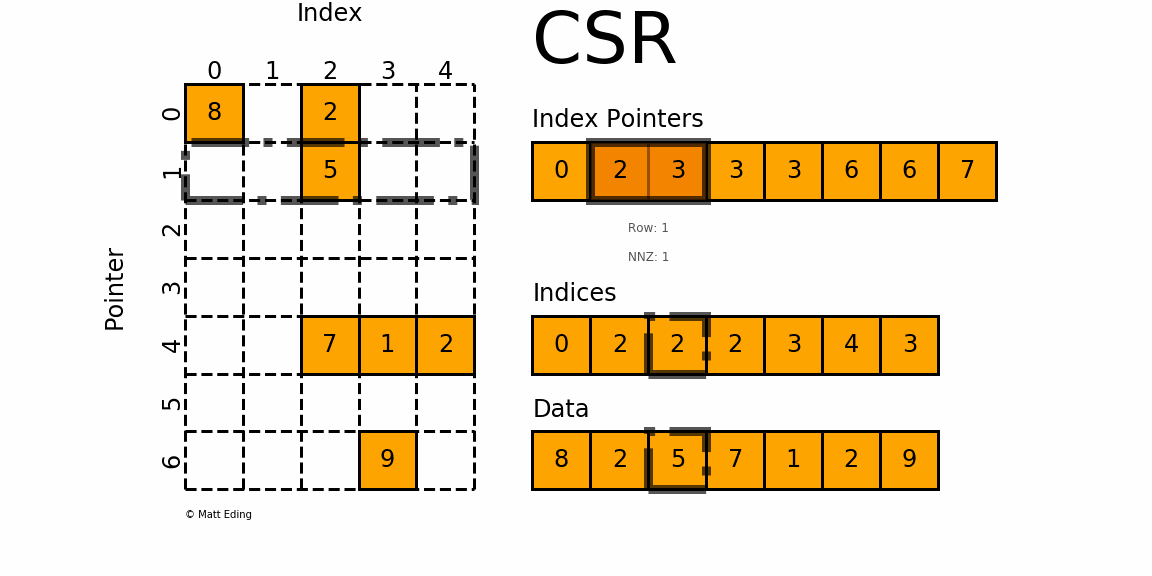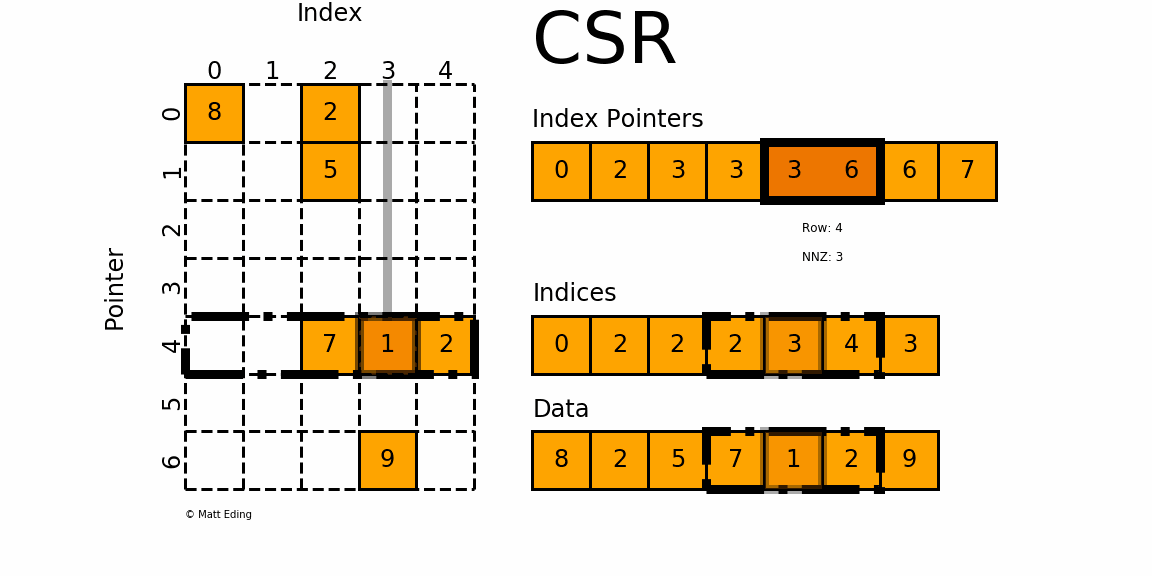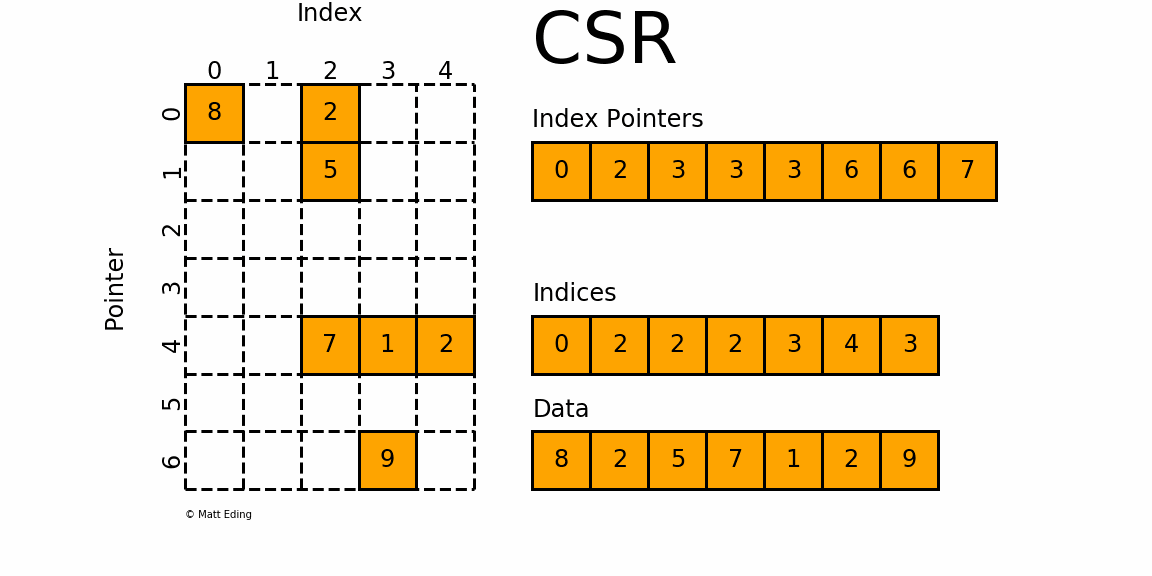
。
csr_matrix可用于各种算术运算:它支持加法,减法,乘法,除法和矩阵幂等操作.
其有五种实例化方法,其中前四种初始化方法类似coo_matrix,即通过密集矩阵构建、通过其他类型稀疏矩阵转化、构建一定shape的空矩阵、通过(row, col, data)构建矩阵.
其第五种初始化方式这是直接体现csr_matrix的存储特征:csr_matrix((data, indices, indptr), [shape=(M, N)]),意思是,矩阵中第i行非零元素的列号为indices[indptr[i]:indptr[i+1]],相应的值为data[indptr[i]:indptr[i+1]] 。
举个例子:
>>> import numpy as np>>> from scipy.sparse import csr_matrix>>> indptr = np.array([0, 2, 3, 6])>>> indices = np.array([0, 2, 2, 0, 1, 2])>>> data = np.array([1, 2, 3, 4, 5, 6])>>> csr = csr_matrix((data, indices, indptr), shape=(3, 3)).toarray()array([[1, 0, 2], [0, 0, 3], [4, 5, 6]])
csr_matrix同样有很多方法,其中tobytes(),tolist(), tofile(),tostring()值得注意,其他具体参考官方文档,csr_matrix对象属性前五个同coo_matrix,另外还有属性如下:
indices 。
与属性data一一对应,元素值代表在某一行的列号 。
indptr 。
csr_matrix各行的起始值,length(csr_object.indptr) == csr_object.shape[0] + 1 。
has_sorted_indices 。
判断每一行的indices是否是有序的,返回bool值 。
csr_matrix的优点:
高效的算术运算CSR + CSR,CSR * CSR等高效的行切片快速矩阵运算 。
csr_matrix的缺点:
列切片操作比较慢(考虑csc_matrix)稀疏结构的转换比较慢(考虑lil_matrix或doc_matrix) 。
csc_matrix和csr_matrix正好相反,即按列压缩的稀疏矩阵存储方式,同样由三个一维数组indptr, indices, data组成,如下图所示:
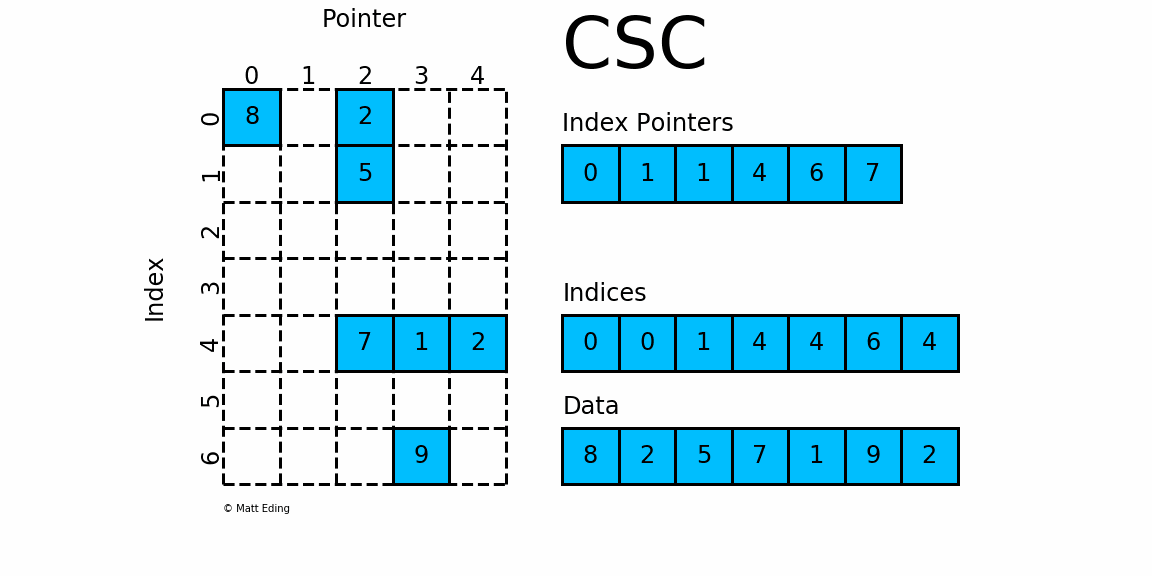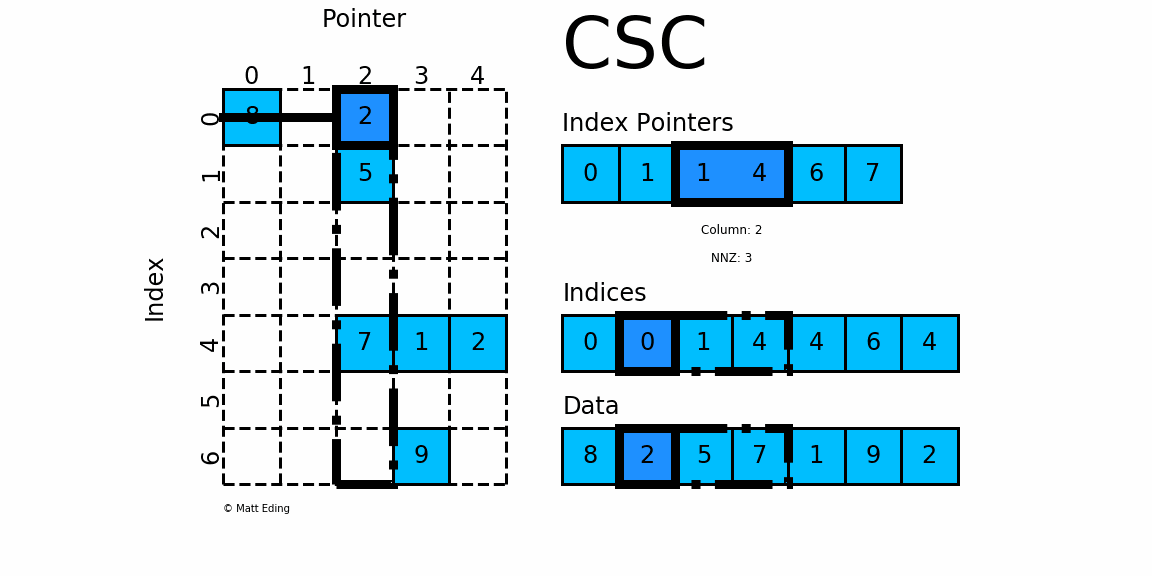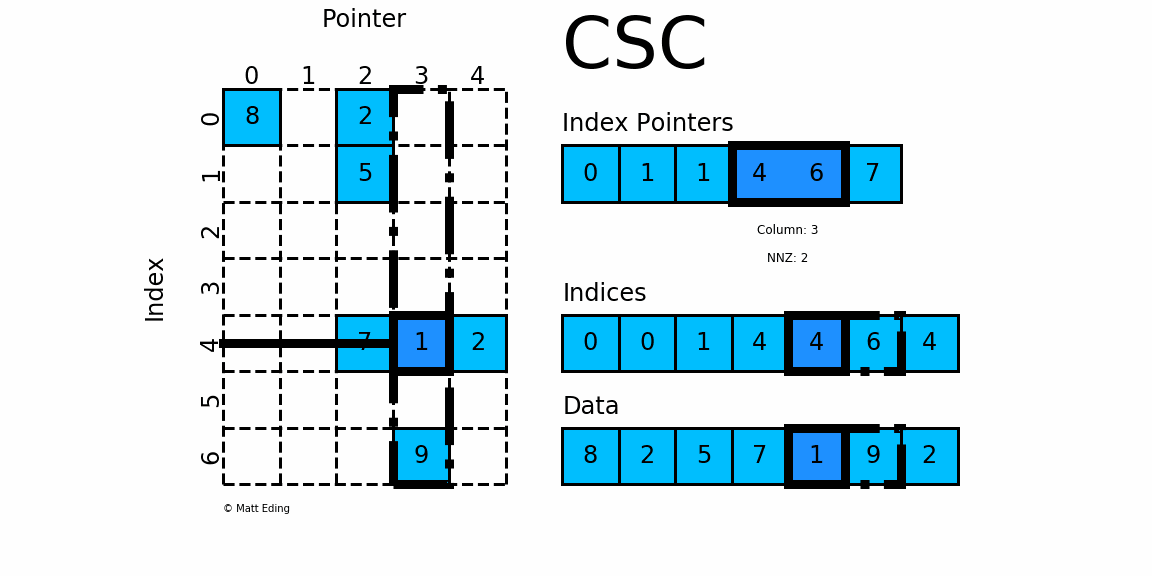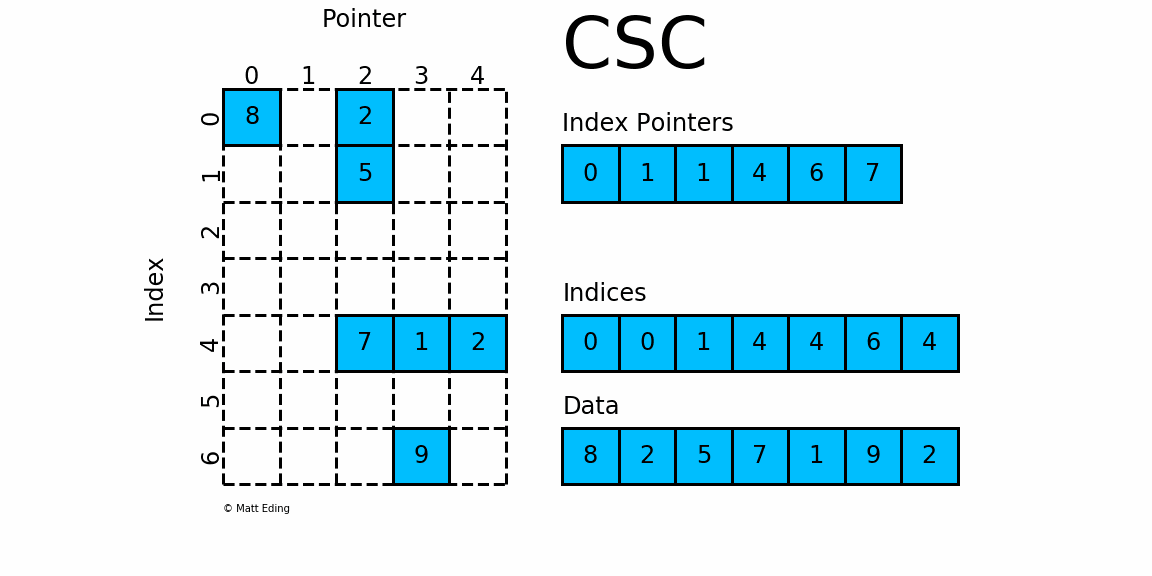
其实例化方式、属性、方法、优缺点和csr_matrix基本一致,这里不再赘述,它们之间唯一的区别就是按行或按列压缩进行存储.
而这一区别决定了csr_matrix擅长行操作;csc_matrix擅长列操作,进行运算时需要进行合理存储结构的选择.
lil_matrix,即List of Lists format,又称为Row-based linked list sparse matrix。它使用两个嵌套列表存储稀疏矩阵:data保存每行中的非零元素的值,rows保存每行非零元素所在的列号(列号是顺序排序的).
这种格式很适合逐个添加元素,并且能快速获取行相关的数据.
其初始化方式同coo_matrix初始化的前三种方式:通过密集矩阵构建、通过其他矩阵转化以及构建一个一定shape的空矩阵.

lil_matrix可用于算术运算:支持加法,减法,乘法,除法和矩阵幂。其属性前五个同coo_matrix,另外还有rows属性,是一个嵌套List,表示矩阵每行中非零元素的列号.
LIL matrix本身的设计是用来方便快捷构建稀疏矩阵实例,而算术运算、矩阵运算则转化成CSC、CSR格式再进行,构建大型的稀疏矩阵还是推荐使用COO格式.
LIL format优点 。
支持灵活的切片操作行切片操作效率高,列切片效率低 。
稀疏矩阵格式之间的转化很高效(tobsr()、tocsr()、to_csc()、to_dia()、to_dok()、to_lil()) 。
LIL format缺点 。
加法操作效率低 (consider CSR or CSC) 。
列切片效率低(consider CSC) 。
矩阵乘法效率低 (consider CSR or CSC) 。
dok_matrix,即Dictionary Of Keys based sparse matrix,是一种类似于coo matrix但又基于字典的稀疏矩阵存储方式,key由非零元素的的坐标值tuple(row, column)组成,value则代表数据值.
dok matrix非常适合于增量构建稀疏矩阵,并一旦构建,就可以快速地转换为coo_matrix.
其属性和coo_matrix前四项同;其初始化方式同coo_matrix初始化的前三种:通过密集矩阵构建、通过其他矩阵转化以及构建一个一定shape的空矩阵.
对于dok matrix,可用于算术运算:它支持加法,减法,乘法,除法和矩阵幂;允许对单个元素进行快速访问( O(1) ); 不允许重复.
>>> import numpy as np>>> from scipy.sparse import dok_matrix>>> np.random.seed(10)>>> matrix = random(3, 3, format="dok", density=0.4)>>> matrix[1, 1] = 33>>> matrix[2, 1] = 10>>> matrix.toarray()array([[ 0. , 0. , 0. ], [ 0. , 33. , 0. ], [ 0.19806286, 10. , 0.22479665]])>>> dict(matrix){(2, 0): 0.19806286475962398, (2, 1): 10.0, (2, 2): 0.22479664553084766, (1, 1): 33.0}>>> isinstance(matrix, dict)True
在上面代码最后可以看到,实际上dok_matrix实例也是dict实例,在实现上继承了dict类.
dia_matrix,全称Sparse matrix with DIAgonal storage,是一种对角线的存储方式.
如下图中,将稀疏矩阵使用offsets和data两个矩阵来表示。offsets表示data中每一行数据在原始稀疏矩阵中的对角线位置k(k>0, 对角线往右上角移动;k<0, 对角线往左下方移动;k=0,主对角线).
该格式的稀疏矩阵可用于算术运算:它们支持加法,减法,乘法,除法和矩阵幂.
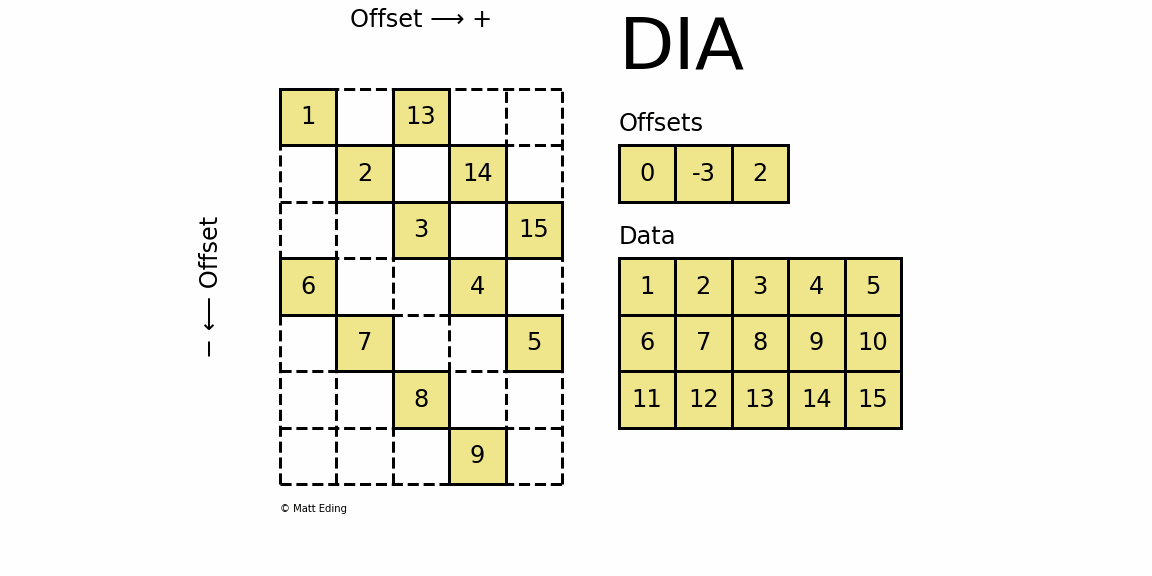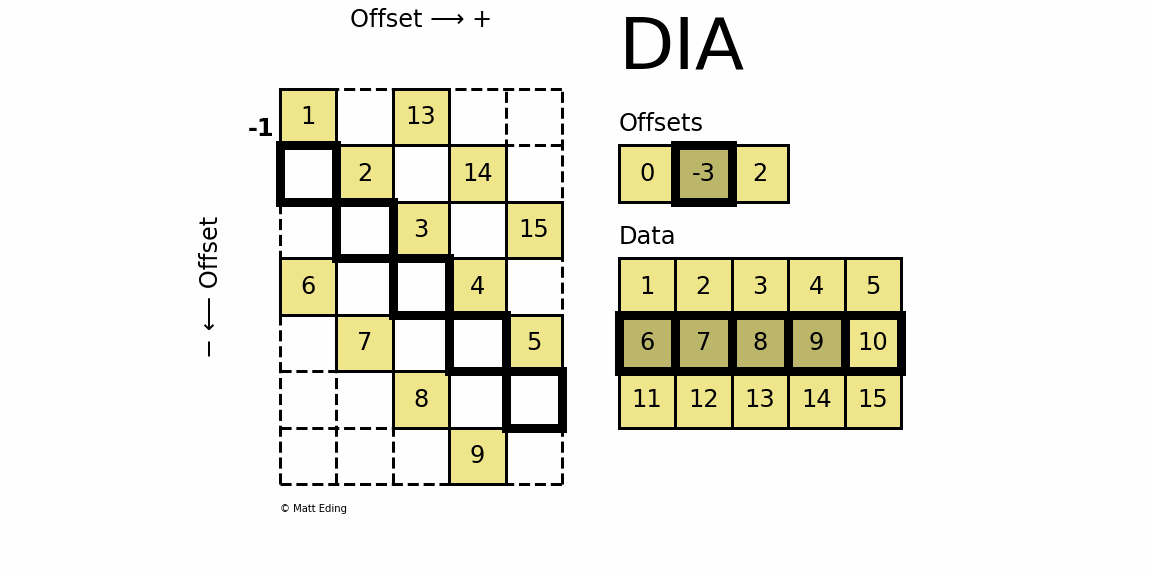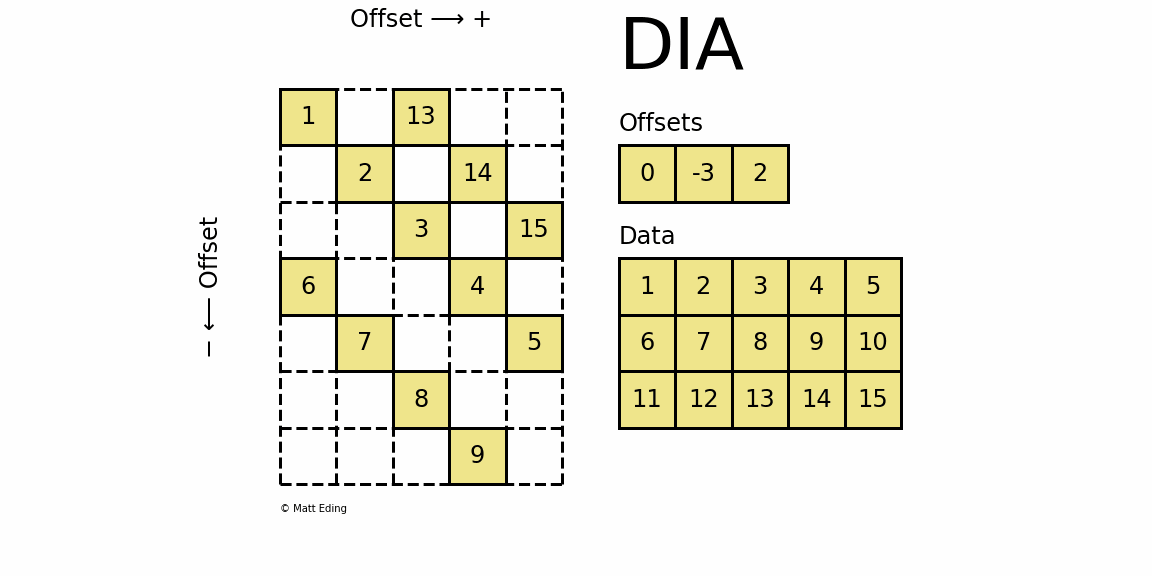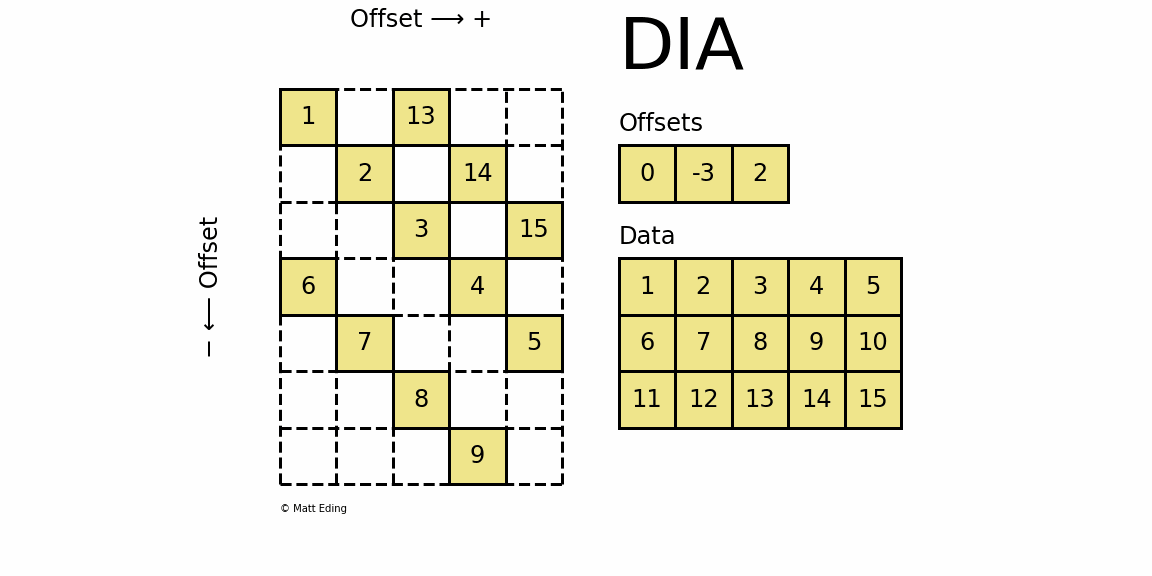
dia_matrix五个属性同coo matrix, 另外还有属性offsets;dia_matrix有四种初始化方式,其中前三种初始化方式同coo_matrix前三种初始化方式,即:通过密集矩阵构建、通过其他矩阵转化以及构建一个一定shape的空矩阵.
第四种初始化方式如下:
dia_matrix((data, offsets), shape=(M, N)) ,
其中,data[k,:]存储着稀疏矩阵offsets[k]对角线上的值 。
>>> data = np.arange(15).reshape(3, -1) + 1>>> offsets = np.array([0, -3, 2])>>> dia = sparse.dia_matrix((data, offsets), shape=(7, 5))>>> dia.toarray()array([[ 1, 0, 13, 0, 0], [ 0, 2, 0, 14, 0], [ 0, 0, 3, 0, 15], [ 6, 0, 0, 4, 0], [ 0, 7, 0, 0, 5], [ 0, 0, 8, 0, 0], [ 0, 0, 0, 9, 0]])
不是很常用,了解即可 。
bsr_matrix,全称Block Sparse Row matrix,这种压缩方式极其类似CSR格式,但使用分块的思想对稀疏矩阵进行按行压缩。所以,BSR适用于具有dense子矩阵的稀疏矩阵。该种矩阵有五种初始化方式,分别如下:
bsr_matrix(D, [blocksize=(R,C)])
D是一个M*N的二维dense矩阵;blocksize需要满足条件:M % R = 0和N % C = 0,若不给定该参数,内部将会应用启发式的算法自动决定一个合适的blocksize. 。
bsr_matrix(S, [blocksize=(R,C)])
S是指其他类型的稀疏矩阵 。
bsr_matrix((M, N), [blocksize=(R,C), dtype])
构建一个shape为M*N的空矩阵 。
bsr_matrix((data, ij), [blocksize=(R,C), shape=(M, N)])
data 和ij 满足条件: a[ij[0, k], ij[1, k]] = data[k] 。
bsr_matrix((data, indices, indptr), [shape=(M, N)])
data.shape一般是k*R*C,其中R、C分别代表block的行和列长,k代表有几个小block矩阵;第i行的块列索引存储在indices[indptr[i]:indptr[i+1]],其值是data[ indptr[i]: indptr[i+1] ].
bsr_matrix可用于算术运算:支持加法,减法,乘法,除法和矩阵幂。如下面的例子,对于许多稀疏算术运算,BSR比CSR和CSC更有效:
>>> from scipy.sparse import bsr_matrix>>> import numpy>>> indptr = np.array([0, 2, 3, 6])>>> indices = np.array([0, 2, 2, 0, 1, 2])>>> data = np.array([1, 2, 3, 4, 5, 6]).repeat(4).reshape(6, 2, 2)>>> bsr_matrix((data,indices,indptr), shape=(6, 6)).toarray()array([[1, 1, 0, 0, 2, 2], [1, 1, 0, 0, 2, 2], [0, 0, 0, 0, 3, 3], [0, 0, 0, 0, 3, 3], [4, 4, 5, 5, 6, 6], [4, 4, 5, 5, 6, 6]])
可以通过热图观察矩阵有没有明显分块模式再决定使不使用该方式 。
bsr matrix对象拥有9个属性,前四个属性与coo matrix相同,另外还有以下属性(注意csr matrix和bsr matrix之间的区别与联系):
data 。
即稀疏矩阵的数组,data.shape一般是k*R*C 。
indices 。
与属性data中的k个二维矩阵一一对应,元素值代表在某一行的列号 。
indptr 。
bsr各行起始起始值 。
blocksize 。
即tuple(R,C) 。
has_sorted_indices 。
判断每一行的indices是否是有序的,返回bool值 。
scipy.sparse模块还包含一些便捷函数,用于快速构建单位矩阵、对角矩阵等,下面做一个简单的汇总:
| 方法 | 用途 |
|---|---|
| identity(n[, dtype, format]) | 生成稀疏单位矩阵 |
| kron(A, B[, format]) | sparse matrices A 和 B的克罗内克积 |
| kronsum(A, B[, format]) | sparse matrices A 和 B的克罗内克和 |
| diags(diagonals[, offsets, shape, format, dtype]) | 构建稀疏对角阵 |
| spdiags(data, diags, m, n[, format]) | 构建稀疏对角阵,同上,但不可指定shape |
| block_diag(mats[, format, dtype]) | mats为iterable, 包含多个矩阵,根据mats构建块对角稀疏矩阵。 |
| tril(A[, k, format]) | 以稀疏格式返回矩阵的下三角部分 |
| triu(A[, k, format]) | 以稀疏格式返回矩阵的上三角部分 |
| bmat(blocks[, format, dtype]) | 从稀疏子块构建稀疏矩阵 |
| hstack(blocks[, format, dtype]) | 水平堆叠稀疏矩阵(column wise) |
| vstack(blocks[, format, dtype]) | 垂直堆叠稀疏矩阵 (row wise) |
| rand(m, n[, density, format, dtype, …]) | 使用均匀分布的值生成给定形状和密度的稀疏矩阵 |
| random(m, n[, density, format, dtype, …]) | 使用随机分布的值生成给定形状和密度的稀疏矩阵 |
| eye(m[, n, k, dtype, format]) | 生成稀疏单位对角阵(默认DIAgonal format) |
scipy.sparse.bmat举例:
In [1]: A = np.arange(8).reshape(2, 4)In [2]: T = np.tri(5, 4)In [3]: L = [[8] * 4] * 2In [4]: I = sparse.identity(4)In [5]: Z = sparse.coo_matrix((2, 3))In [6]: sp.bmat([[ A, Z, L], ...: [None, None, I], ...: [ T, None, None]], dtype=int)Out[7]:<11x11 sparse matrix of type "<class "numpy.int64">" with 33 stored elements in COOrdinate format>In [8]: _.toarray() # ipython previous outputOut[9]:array([[0, 1, 2, 3, 0, 0, 0, 8, 8, 8, 8], [4, 5, 6, 7, 0, 0, 0, 8, 8, 8, 8], [0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0], [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1], [1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0], [1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0]])
scipy.sparse模块还包含一些判断稀疏矩阵类型的函数,这里需要注意的是,issparse() 和 isspmatrix() 是相同的函数,也许是由于历史原因保留下来了两个.
isspars(x)isspmatrix(x)isspmatrix_csc(x)isspmatrix_csr(x)isspmatrix_bsr(x)isspmatrix_lil(x)isspmatrix_dok(x)isspmatrix_coo(x)isspmatrix_dia(x)
load_npz(file) 从.npz文件中读取稀疏矩阵 。
save_npz(file, matrix[,compressed]) 将稀疏矩阵写入.npz文件中 。
其他 。
find(A) 返回稀疏矩阵中非零元素的索引以及值 。
要有效地构造矩阵,请使用dok_matrix或lil_matrix 。
lil_matrix类支持基本切片和花式索引,其语法与NumPy Array类似;lil_matrix形式是基于row的,因此能够很高效的转为csr,但是转为csc效率相对较低.
强烈建议不要直接使用NumPy函数运算稀疏矩阵 。
如果你想将NumPy函数应用于这些矩阵,首先要检查SciPy是否有自己的给定稀疏矩阵类的实现,或者首先将稀疏矩阵转换为NumPy数组(使用类的toarray()方法).
要执行乘法或转置等操作,首先将矩阵转换为CSC或CSR格式,效率高 。
CSR格式特别适用于快速矩阵矢量产品 。
CSR,CSC和COO格式之间的所有转换都是线性复杂度.
以上为个人经验,希望能给大家一个参考,也希望大家多多支持我.
原文链接:https://blog.csdn.net/jeffery0207/article/details/100064602 。
最后此篇关于python scipy 稀疏矩阵的使用说明的文章就讲到这里了,如果你想了解更多关于python scipy 稀疏矩阵的使用说明的内容请搜索CFSDN的文章或继续浏览相关文章,希望大家以后支持我的博客! 。
我在网上搜索但没有找到任何合适的文章解释如何使用 javascript 使用 WCF 服务,尤其是 WebScriptEndpoint。 任何人都可以对此给出任何指导吗? 谢谢 最佳答案 这是一篇关于
我正在编写一个将运行 Linux 命令的 C 程序,例如: cat/etc/passwd | grep 列表 |剪切-c 1-5 我没有任何结果 *这里 parent 等待第一个 child (chi
所以我正在尝试处理文件上传,然后将该文件作为二进制文件存储到数据库中。在我存储它之后,我尝试在给定的 URL 上提供文件。我似乎找不到适合这里的方法。我需要使用数据库,因为我使用 Google 应用引
我正在尝试制作一个宏,将下面的公式添加到单元格中,然后将其拖到整个列中并在 H 列中复制相同的公式 我想在 F 和 H 列中输入公式的数据 Range("F1").formula = "=IF(ISE
问题类似于this one ,但我想使用 OperatorPrecedenceParser 解析带有函数应用程序的表达式在 FParsec . 这是我的 AST: type Expression =
我想通过使用 sequelize 和 node.js 将这个查询更改为代码取决于在哪里 select COUNT(gender) as genderCount from customers where
我正在使用GNU bash,版本5.0.3(1)-发行版(x86_64-pc-linux-gnu),我想知道为什么简单的赋值语句会出现语法错误: #/bin/bash var1=/tmp
这里,为什么我的代码在 IE 中不起作用。我的代码适用于所有浏览器。没有问题。但是当我在 IE 上运行我的项目时,它发现错误。 而且我的 jquery 类和 insertadjacentHTMl 也不
我正在尝试更改标签的innerHTML。我无权访问该表单,因此无法编辑 HTML。标签具有的唯一标识符是“for”属性。 这是输入和标签的结构:
我有一个页面,我可以在其中返回用户帖子,可以使用一些 jquery 代码对这些帖子进行即时评论,在发布新评论后,我在帖子下插入新评论以及删除 按钮。问题是 Delete 按钮在新插入的元素上不起作用,
我有一个大约有 20 列的“管道分隔”文件。我只想使用 sha1sum 散列第一列,它是一个数字,如帐号,并按原样返回其余列。 使用 awk 或 sed 执行此操作的最佳方法是什么? Accounti
我需要将以下内容插入到我的表中...我的用户表有五列 id、用户名、密码、名称、条目。 (我还没有提交任何东西到条目中,我稍后会使用 php 来做)但由于某种原因我不断收到这个错误:#1054 - U
所以我试图有一个输入字段,我可以在其中输入任何字符,但然后将输入的值小写,删除任何非字母数字字符,留下“。”而不是空格。 例如,如果我输入: 地球的 70% 是水,-!*#$^^ & 30% 土地 输
我正在尝试做一些我认为非常简单的事情,但出于某种原因我没有得到想要的结果?我是 javascript 的新手,但对 java 有经验,所以我相信我没有使用某种正确的规则。 这是一个获取输入值、检查选择
我想使用 angularjs 从 mysql 数据库加载数据。 这就是应用程序的工作原理;用户登录,他们的用户名存储在 cookie 中。该用户名显示在主页上 我想获取这个值并通过 angularjs
我正在使用 autoLayout,我想在 UITableViewCell 上放置一个 UIlabel,它应该始终位于单元格的右侧和右侧的中心。 这就是我想要实现的目标 所以在这里你可以看到我正在谈论的
我需要与 MySql 等效的 elasticsearch 查询。我的 sql 查询: SELECT DISTINCT t.product_id AS id FROM tbl_sup_price t
我正在实现代码以使用 JSON。 func setup() { if let flickrURL = NSURL(string: "https://api.flickr.com/
我尝试使用for循环声明变量,然后测试cols和rols是否相同。如果是,它将运行递归函数。但是,我在 javascript 中执行 do 时遇到问题。有人可以帮忙吗? 现在,在比较 col.1 和
我举了一个我正在处理的问题的简短示例。 HTML代码: 1 2 3 CSS 代码: .BB a:hover{ color: #000; } .BB > li:after {

我是一名优秀的程序员,十分优秀!