个人中心
文章发布
退出
作者热门文章
- ubuntu12.04环境下使用kvm ioctl接口实现最简单的虚拟机
- Ubuntu 通过无线网络安装Ubuntu Server启动系统后连接无线网络的方法
- 在Ubuntu上搭建网桥的方法
- ubuntu 虚拟机上网方式及相关配置详解
27
4
CFSDN坚持开源创造价值，我们致力于搭建一个资源共享平台，让每一个IT人在这里找到属于你的精彩世界.
这篇CFSDN的博客文章numpy基础教程之np.linalg由作者收集整理，如果你对这篇文章有兴趣，记得点赞哟.
前言 。
numpy.linalg模块包含线性代数的函数。使用这个模块，可以计算逆矩阵、求特征值、解线性方程组以及求解行列式等。本文讲给大家介绍关于numpy基础之 np.linalg的相关内容，下面话不多说了，来一起看看详细的介绍吧 。
（1）np.linalg.inv()：矩阵求逆 。
（2）np.linalg.det()：矩阵求行列式（标量） 。
np.linalg.norm 。
顾名思义，linalg=linear+algebra linalg=linear+algebra\mathrm{linalg=linear + algebra}，norm norm\mathrm{norm}则表示范数，首先需要注意的是范数是对向量（或者矩阵）的度量，是一个标量（scalar）:
首先help(np.linalg.norm)查看其文档:
norm(x, ord=none, axis=none, keepdims=false)1 。
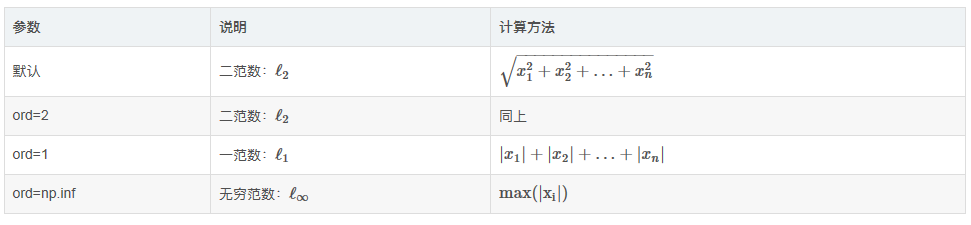
这里我们只对常用设置进行说明，x x\mathrm{x}表示要度量的向量，ord ord\mathrm{ord}表示范数的种类， 。
|
1
2
3
4
5
6
7
8
9
|
>>> x
=
np.array([
3
,
4
])
>>> np.linalg.norm(x)
5.
>>> np.linalg.norm(x,
ord
=
2
)
5.
>>> np.linalg.norm(x,
ord
=
1
)
7.
>>> np.linalg.norm(x,
ord
=
np.inf)
4123456789
|
范数理论的一个小推论告诉我们：ℓ 1 ≥ℓ 2 ≥ℓ ∞ ℓ1≥ℓ2≥ℓ∞ 。
总结 。
以上就是这篇文章的全部内容了，希望本文的内容对大家的学习或者工作具有一定的参考学习价值，如果有疑问大家可以留言交流，谢谢大家对我的支持.
原文链接：https://blog.csdn.net/lanchunhui/article/details/51004387 。
最后此篇关于numpy基础教程之np.linalg的文章就讲到这里了,如果你想了解更多关于numpy基础教程之np.linalg的内容请搜索CFSDN的文章或继续浏览相关文章，希望大家以后支持我的博客！ 。
27
4
0
vue3 快速入门系列 - 基础 前面我们已经用 vue2 和 react 做过开发了。 从 vue2 升级到 vue3 成本较大，特别是较大的项目。所以许多公司对旧项目继续使用vue2，新项目则
C# 基础 C#项目创建 这里注意win10虚拟机需要更新下补丁，不然直接下载visual studio 2022会显示版本不支持 HelloWorld C#的类文件都是以.cs结尾，入口方法为sta
关于 iPhone 内存管理的非常基本的问题: 假设我有一个 viewController，其中有几个 subview 也由 viewController 控制。当我删除顶部 viewControll
我仍在努力适应指针。不是概念——我理解内存位置、匹配可变长度的指针增量等——这是语法。这是一个我认为是我感到困惑/无法直观把握的原因之一: int a = 42; 在一个int大小的内存空间中分配并放
1. 简介 Kafka（Apache Kafka） 是一种分布式流数据平台，最初由LinkedIn开发，并于后来捐赠给Apache软件基金会，成为了一个Apache顶级项目。它被设计用于处理大规
1.想要在命令提示符下操作mysql服务器，添加系统变量。（计算机-系统属性——环境变量——path） 2.查询数据表中的数据； select selection_lis
MySQL表的增删改查(基础) 1. CRUD 注释：在SQL中可以使用“–空格+描述”来表示注释说明 CRUD 即增加(Create)、查询(Retrieve)、更新(Update)、删除(Dele
我有一个网页，可以在加载时打开显示模式，在这个模式中，我有一个可以打开第二个模式的链接。当第二个模式关闭时(通过单击关闭按钮或单击模式外部)，我想重新打开第一个模式。 对于关闭按钮，我可以通过向具有
使用 Core Data Fetched Properties，我如何执行这个简单的请求: 我希望获取的属性 ( myFetchProp ) 存储 StoreA ，它应该这样做: [myFetchPr
关闭。这个问题是opinion-based .它目前不接受答案。 想改进这个问题？更新问题，以便 editing this post 可以用事实和引用来回答它. 8年前关闭。 Improve this
最近，我得到了一个现有的Drupal项目，并被要求改进前端(HTML，JavaScript，CSS)。我在Django，PHP，Ruby等方面具有大量的前端和后端开发经验，但是我没有任何Drupal经
我试图让我的用户通过使用扫描仪类来决定要做什么，但我有一个问题，代码一旦运行就不会激活，并且它不会让我跳过任何行。我的代码如下所示: Scanner input = new Scanner(S
对模糊的标题表示歉意，因为我想不出这个名字是什么。 基本上创建一个计算学生财务付款的小程序。当我运行它时，它计算对象限额没有问题。然而，无论我尝试什么，对象“助学金”似乎除了 0 之外什么也没有提出。
这是我的代码 - main() { double x; double y = pow(((1/3 + sin(x/2))(pow(x, 3) + 3)), 1/3); prin
如果我的术语在这个问题上有误，我们深表歉意。 采取以下功能: i = 1; v = i * 2; for (j = 0; j < 4; j++ ) { console.log(v);
我的应用程序中有不同的类文件。我有 5 个类，其中 2 个是 Activity ，1 个是运行的服务。其他 2 个只是类。这两个类中变量的生命周期是多少。我知道一个 Activity 可以被操作系统杀
例如，一个方法返回一个 List 类型的对象。 public List bojangles () ... 一些代码调用方法FooBar.bojangles.iterator(); 我是 Java 的新
我遇到了一个奇怪的问题，网格的大小不适合我的屏幕。当我使用 12 列大时，它只占据屏幕的 1/3 的中间，请参见图像。我不确定是什么导致了这个问题。我没有任何会导致这种情况发生的奇怪 CSS。我不会在
我尝试使用头文件和源文件，但遇到了问题。因此，我对我正在尝试做的事情做了一个简化版本，我在 CodeBlocks 中遇到了同样的错误(undefined reference to add(double
我正在为我的网格系统使用基础，但这在任何网格系统中都可能是一个问题。我基本上用一个容器包裹了 3 个单元格，但其中一个单元格应该长到页面边框(留在我的 Sampe-Image 中)但这也可能在右侧)。
我是一名优秀的程序员,十分优秀！