CFSDN坚持开源创造价值，我们致力于搭建一个资源共享平台，让每一个IT人在这里找到属于你的精彩世界.

这篇CFSDN的博客文章我们一起学习RSA-PSS 算法由作者收集整理，如果你对这篇文章有兴趣，记得点赞哟.

  。

AS(5)：RSA-PSS 算法简介 。

2018年发布的 TLS v1.3(TLS：Transport Layer Security，传输安全层协议，TLS v1.3 对应 RFC 8446)中，其支持的数字签名算法有：RSASSA-PKCS1-v1_5、RSASSA-PSS、ECDSA(Elliptic Curve Digital Signature Algorithm，椭圆曲线签名算法)、EdDSA(Edwards-Curve Digital Signature Algorithm，爱德华曲线签名算法).

这些算法已经是标准(或者是事实上的标准)，不过从某种意义上说，这些算法也代表着美国签名算法流派.

除美国外，俄罗斯在1994年发布数字签名算法标准 GOST R 34.10-94，并在2001年发布椭圆曲线数字签名算法标准GOST R34.10- 2001。GOST R34.10-2001在2012年更新为 GOST R34.10-2012。韩国在1998年发表韩国基于证书的数字签名算法 KCDSA 和 EC- KCDA，对应标准发布于[88,89]。德国在 2005 年发布德国椭圆曲线数字签名算法标准 EC- GDSA。中国在 2012 年发布 SM2 椭圆曲线数字签名算法标准，在 2016 年发布 SM9 标识密码数字签名算法标准.

作为重要的国际标准化组织，ISO/IEC 同样也发布了一系列的数字签名算法标准：ISO/IEC 9796、ISO/ IEC 14888、ISO/IEC 20008、ISO/IEC 18370、ISO/IEC 23264 等等.

弱水三千，只取一瓢。由于文章主题和篇幅的关系，本文只介绍 RSASA-PSS 算法.

PSS (Probabilistic Signature Scheme，概率签名方案)是私钥签名的一种填充方式。RSASA(RSA Signature Algorithm，RSA 数字签名算法)目前支持两种算法：RSASSA-PKCS1-v1_5、RSASSA-PSS。由于安全的原因，RSASSA-PKCS1-v1_5 现在的使用场景仅仅是为了兼容(可以参考《童话里都是骗人的》、《梦被批得离离散散》、《蜀道难，难于上青天》)，当前主流推荐使用 RSASSA-PSS 算法.

PSS 方案首先由 Bellare和Rogaway 首先提出，PSS 与 OAEP(Optimal Asymmetric Encryption Padding，最优非对称加密填充)非常相像，当然 OAEP也是由这两位大神提出的(OAEP 请参见《蜀道难，难于上青天》).

Mihir Bellare是加州大学圣地亚哥分校(UCSD，University of California, San Diego)计算机科学与工程系的教授。Bellare 于1986年在加州理工学院获得学士学位，1991年在麻省理工学院获得博士学位。1991年至1995年，Bellare 在IBM担任研究员 Bellare 是HMAC、RSA-OAEP、RSA-PSS和OCB的联合开发者。Bellare 是 ACM 和 IACR 的研究员。他曾获得 ACM 巴黎Kanellakis 理论与实践奖，RSA 会议数学奖，David 和 Lucille Packard基金会科学与工程奖学金，以及NSF职业奖( He has received an ACM Paris Kanellakis Theory and Practice Award, an RSA Conference Award in Mathematics, a David and Lucille Packard Foundation Fellowship in Science and Engineering, and an NSF Career award).

Phillip Rogaway 是美国加州大学戴维斯分校(UCD，University of California, Davis)计算机科学系的教授。Rogaway 本科毕业于加州大学伯克利分校(UCB，University of California, Berkeley)，并于1991年到麻省理工计算理论小组攻读博士学位(MIT s Theory of Computation group )。博士毕业之后，Rogaway 到 IBM 担任安全架构师，然后于1994年到 UCD 工作。Rogaway 获得过 Levchin 奖(2016)，PET 奖(2015)，IACR 研究员(2012)，ACM巴黎 Kanellakis 奖(2009)，RSA 数学奖(2003)(Levchin prize (2016), PET Award (2015), IACR Fellow (2012), ACM Paris Kanellakis Award (2009), RSA Award in Mathematics (2003)).

图1 Bellare(左)和 Rogaway(右) 。

RSA 数字签名算法(RSASA)的本质，仍然是 RSA 加密/解密算法，如图2所示.

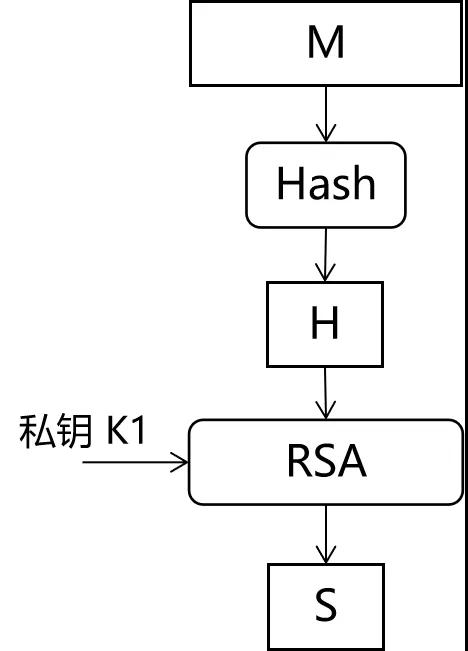
图2 RSA 数字签名算法示意 。

从图2可以看到，RSSSA 分为两步.

1)将待签名的 M 进行 Hash，从而得到 H 。

2)将 H 进行 RSA 私钥加密 。

既然是 RSA 加密，就绕不开 RSA 那个致命问题——能够非常简单地被选择密文攻击所破解(具体请参见《童话里都是骗人的》)，于是也就引发了 RSA 填充算法.

RSASSA-PKCS1-v1_5 采用的就是 RSA_PKCS1_PADDING_v1_5 填充算法，而 RSASSA-PSS 的填充算法则与 RSA_PKCS1_OAEP_PADDING 填充算法比较相像。下面我们就介绍 RSASSA-PSS 算法.

1、RSASSA-PSS 的填充算法

  。

RSASSA-PSS 算法本质就是在 RSA 算法的基础上叠加上一种填充算法(为了便于表述，这种填充算法也可以称为 RSA-PSS 填充算法，或者 RSA-PSS 编码)，如图3所示.

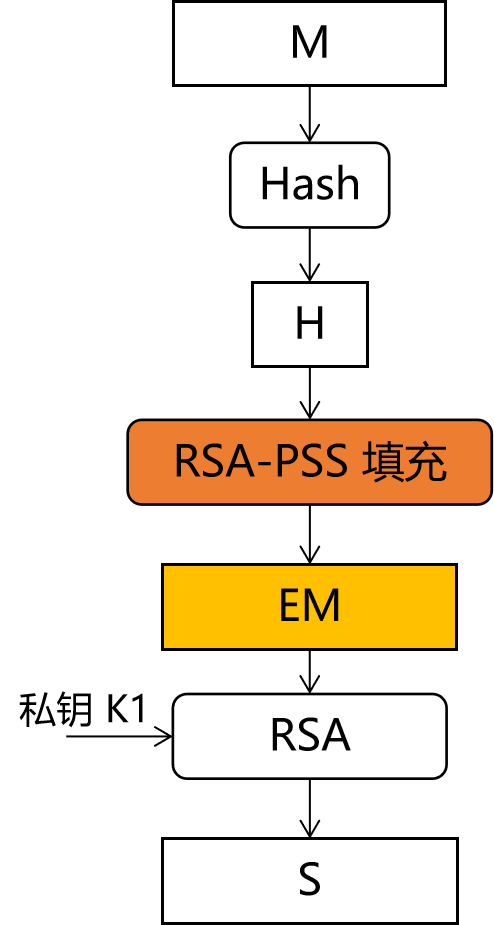
图3 RSA-PSS 数字签名算法示意 。

图3中，在 Hash 之后，在 RSA 之前，RSASA-PSS 算法插入了一个 RSA-PSS 填充算法。RSA-PSS 的具体算法，如图4所示.

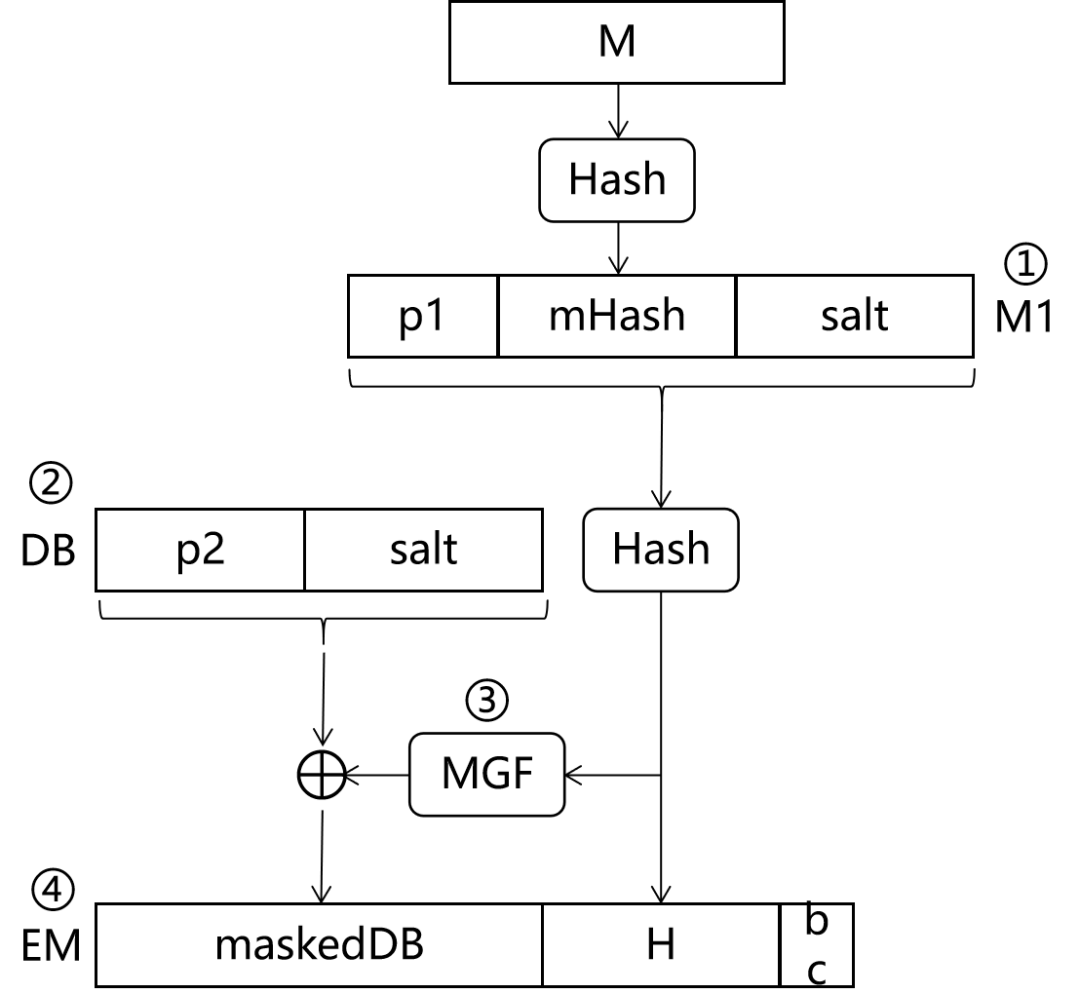
图4 RSA-PSS 填充算法示意 。

图4中，RSA-PSS 填充算法，分为四步。下面我们分别讲述这四步.

1.1 M 转换成 M1 。

通过图4可以看到， 。

M1 = p1 || mHash || salt 。

p1 就是8字节的0.

mHash = Hash(M)，M 是待签名的消息，Hash 算法当前的选择是 SHA-1。SHA-1 的输出是20个字节，所以 mHash 的长度 。

hLen = 20 。

salt(盐值)就是一个伪随机数，它的长度(记为 sLen)一般等于 hLen，当前的选择就是 。

sLen = hLen 。

1.2 构建 DB 。

DB(Data Block)的构建方式为， 。

DB = p2 || salt 。

p2 的值等于若干个字节的 0x00 后面跟着1字节的 0x01。这若干个字节记为 xLen，则 xLen 等于， 。

xLen = emLen - sLen - hLen - 2 。

其中，emLen 是图4中 EM 的长度 。

salt 的值等于1.1节所描述的 salt 的值。特别强调，两者必须相等，否则无法验证数字签名(具体请参见下面第三节：RSASSA-PSS 的数字签名验证) 。

1.3 MGF 。

MGF(Mask Generation Function，掩码生成函数)的相关介绍，请参见《蜀道难，难于上青天》，这里就不再重复。另外，RSA-PSS 所采用的 MGF 函数的输出，也是 MGF1.

对于图4而言，MGF 所对应的输入和输出分别是 。

mask = MGF1(mgfSeed, maskLen, hash) 。

其中， 。

mgfSeed = Hash(M1)，Hash 函数选择 SHA-1 。

maskLen = emLen - hLen - 1 。

hash 函数选择 SHA-1 。

1.4 构建 EM 。

EM(Encoded Message)的值等于， 。

EM = maskedDB || H || bc 。

其中， 。

maskedDB = DB xor mask 。

H = Hash(M1) 。

bc = 0xBC 。

其中，bc 的长度是1个字节，H 的长度是 hLen，maskedDB 的长度(记为 mdbLen)为 。

mdbLen = emLen - hLen - 1 。

其中，emLen 的长度就是 EM 的长度。由于接下来要对 EM 进行 RSA 加密计算，所以 EM 的长度满足 RSA 的要求即可.

2、RSASA-PSS 的签名算法

  。

经过 RSA-PSS 填充以后，接下来的签名算法，就比较简单了， 。

EM = RSA-PSS(M) 。

S = RSAEP(EM) 。

RSA 算法，请参见《RSA 基本算法》、《RSA 的计算方法》，这里不再重复.

3、RSASA-PSS 的签名验证

  。

RSASA-PSS 签名验证，分为如下几个步骤.

3.1 解密 。

RSASA-PSS 的签名验证，首先是解密， 。

EM = RSADP(S) 。

也即，拿到签名 S 以后，运行 RSA 解密算法，得到解密后的信息 EM.

3.2 分割 EM 。

得到 EM 以后，接下来就是分割和验证， 。

maskedDB, H, bc = Split(EM) 。

最右一个字节是 bc，然后从 bc 往左数 hLen 个字节是 H，然后剩下的是 maskedDB.

如果最右一个字节不是 0xBC，则签名验证停止(该数字签名是非法的).

3.3 计算 salt 。

得到 H 以后，就可以计算 mask， 。

mask = MGF1(H, maskLen, hash) 。

因为， 。

maskedDB = DB xor mask 。

所以， 。

DB = maskedDB xor mask 。

得到 DB 以后，就可以对其分割 。

p2, salt = Split(DB) 。

其中，salt 是 DB 的最右 sLen 个字节，剩下的是 p2.

如果 p2 的值不等于若干个字节的 0x00 后面跟着1字节的 0x01，那么验证停止(该数字签名是非法的).

3.4 校验 Hash 。

通过所接收到的 M，计算 Hash 。

mHash = Hash(M) 。

然后构建 M1 。

M1 = p1 || mHash || salt 。

其中，salt 就是 3.3 步所计算出的 salt 。

再然后，计算 M1 的 Hash 。

H1 = Hash(M1) 。

比较 H1 与 H，如果两者相等，则签名验证通过。如果不相等，则签名非法.

其中，H 就是3.2步所得到的哈希值.

经过以上四步以后，就完成了 RSASA-PSS 的数字签名验证.

原文链接：https://mp.weixin.qq.com/s/zgYZs-soAuM0-C_m35Ay0g 。

最后此篇关于我们一起学习RSA-PSS 算法的文章就讲到这里了,如果你想了解更多关于我们一起学习RSA-PSS 算法的内容请搜索CFSDN的文章或继续浏览相关文章，希望大家以后支持我的博客！ 。