个人中心
gpt4 book ai didi

C++用Dijkstra(迪杰斯特拉)算法求最短路径

转载 作者：qq735679552 更新时间：2022-09-27 22:32:09 28 4
gpt4 key购买 nike

CFSDN坚持开源创造价值，我们致力于搭建一个资源共享平台，让每一个IT人在这里找到属于你的精彩世界.

这篇CFSDN的博客文章C++用Dijkstra(迪杰斯特拉)算法求最短路径由作者收集整理，如果你对这篇文章有兴趣，记得点赞哟.

算法介绍 。

迪杰斯特拉算法是由荷兰计算机科学家狄克斯特拉于1959 年提出的，因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法，解决的是有向图中最短路径问题。迪杰斯特拉算法主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。Dijkstra算法能得出最短路径的最优解，但由于它遍历计算的节点很多，所以效率低.

算法思想 。

按路径长度递增次序产生算法:

　把顶点集合V分成两组:

　　（1）S：已求出的顶点的集合（初始时只含有源点V0） 。

　　（2）V-S=T：尚未确定的顶点集合 　　将T中顶点按递增的次序加入到S中，保证:

　　（1）从源点V0到S中其他各顶点的长度都不大于从V0到T中任何顶点的最短路径长度 。

　　（2）每个顶点对应一个距离值 。

　　S中顶点：从V0到此顶点的长度 。

　　T中顶点：从V0到此顶点的只包括S中顶点作中间顶点的最短路径长度 。

　　依据：可以证明V0到T中顶点Vk的，或是从V0到Vk的直接路径的权值；或是从V0经S中顶点到Vk的路径权值之和 。

应用举例 。

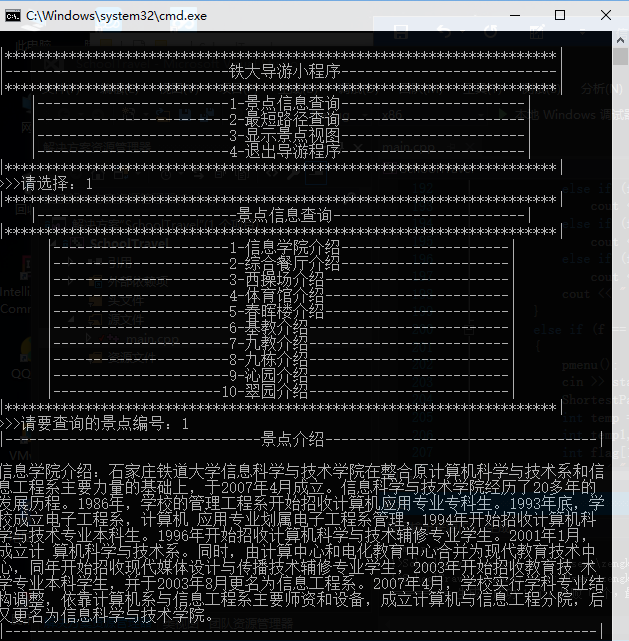
（1）题目：编写一个校园导游程序，为来访的客人提供各种信息查询服务.

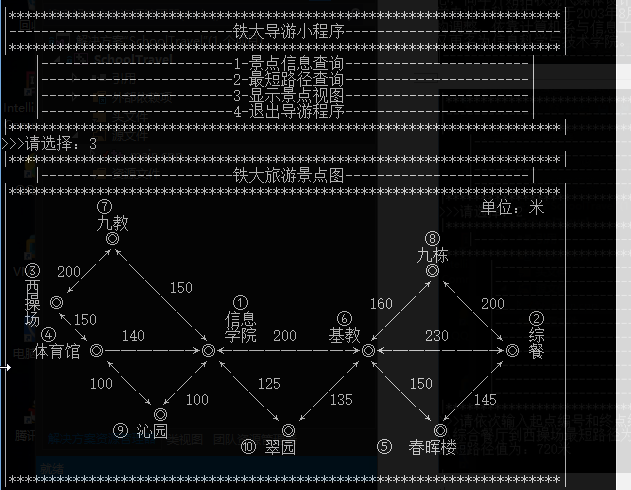
　　　　主要功能：1.设计学校的校园平面图，所含景点不少于10个：顶点表示景点，边表示路径等； 。

　　　　　　　　　2.为客人提供图中任意景点相关信息的查询； 。

　　　　　　　　　3.为客人提供图中任意景点的问路查询，即查询人以景点间的一条最短路径.

　　　　　　要求：1.设计一个主界面； 。

　　　　　　        2.设计功能菜单，供用户选择 。

　　　　　　        3.有一定的实用性.

（2）设计思路:

　　1、该题主要有算法思路以及程序的逻辑思路，首先从逻辑思路讲，进入程序，首先设计一个主菜单，选项有景点信息查询，最短路径查询以及显示景点的平面视图三个子菜单，然后根据用户的输入选择的子菜单前的编号，分进入不同的子菜单；该功能是由if….else if…. 语句实现。在景点信息查询和最短路径查询子菜单下还有二级子菜　单，都是列 出所有景点并在前面编号，查询景点信息时，输入景点前面的编号即可，查询最短路径时，先输入起点的编号，再输入终点的编号。而显示景点视图则调用景点平面图函数即可显 示.

　　2、算法思路主要是迪杰斯特拉算法的思路，利用迪杰斯特拉算法求最短路径.

　　3、先定义好图的储存结构，本题采用邻接矩阵的方式来表示图，并在主函数中初始化该图； 。

　　4、定义三个全局一维数组，一个bool类型数组S[]用来记录从v0到vi是否已经确定了最短路径，是则记S[i]=true ,否记S[i]= flase；一个int 类型数组Path[]用来记录从v0到vi的当前最短路径上的vi的直接前驱顶点编号，若v 到vi之间有边则记Path[i] = v的编号，否则记Path[i] = -1；最后一个数组D[]用来记录从v0到vi之间的最短路径长度，存在则记v0到vi之间边的权值或者权值和，否则记为MAX 。

　　5、定义一个求最短路径的函数，传入的参数为图和起点，首先进行初始化工作，初始化S[]数组全为false，D[]数组初始化为起点到各个顶点的权值，Path[]数组初始化为起点是否与各顶点有边，有则记v0否则记-1； 。

　　6、然后进行n-1次for循环，找出vo到其余n-1个顶点之间的最短路径，比较当前D[]数组中最小值，找到最小值的编号v，该编号就是从v0出发到所有顶点中距离最短的顶点编号，然后把S[v]的值置为true。说明从v0出发到顶点v已经找到最短路径； 。

　　7、接着就要更新D[]数组，因为D[]数组是记录最短路径的，现在已经找到了一个顶点的最短路径，已该顶点v为中间点，判断从该顶点v出发到剩下的顶点的路径长度加上该点到v0的路径长度是否小于直接从v0出发到其余顶点的路径长度，如果小于，则更新D[i]为以该顶点v为中间点求得的路径长度。更新Path[i] = v；即i的前驱不再是v0而是v,

　　8、循环（6）（7）两步n-1次即可得到D[]数组，输出D[]数组既是v0到所有顶点的最短路径长度； 。

（3）源代码:

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
#include<iostream>
#include<fstream>
#include<string>
using namespace std;
/**
  *作者：Dmego
  *时间：2016-12-12
  */
#define MAX 1000000 //表示极大值∞
#define max 10
bool S[max]; //记录从源点V0到终点Vi是否已经确定为最短路径，确定了记true，否则记false
int Path[max]; //记录从源点V0到终点Vi的当前最短路径上终点Vi的直接前驱顶点序号，若V0到Vi之间有边前驱为V0否则为-1
int D[max]; //记录源点到终点之间最短路径的长度，存在记V0到Vi的边的权值，否则记为MAX
typedef struct
{
  string vexs[max]; //顶点表
  int arcs[max][max]; //邻接矩阵
  int vexnum, arcnum; //图当前点数和边数
 
}AMGraph;
//利用迪杰斯特拉算法求最短路径
void ShortestPath_DIJ(AMGraph &G, int v0)
{ //使用迪杰斯特拉算法求有向网G中的V0 定点到其余顶点的最短路径
  int n = G.vexnum; //顶点数
  for ( int v = 0; v < n; v++) //n个顶点依次初始化
  {
  S[v] = false ; //S初始化为空集
  D[v] = G.arcs[v0][v]; //将v0到各个终点的最短路径长度初始化为边上的权值
  if (D[v] < MAX)
   Path[v] = v0; //如果v0和v之间有边，则将v的前驱初始化为v0
  else
   Path[v] = -1; //如果v0和v之间无边，则将v的前驱初始化为-1
  }
  S[v0] = true ; //将v0加入s
  D[v0] = 0; //源点到源点的权值为0
  //---------初始化结束，开始主循环，每次求得v0到某个顶点的最短路径，将v加到S数组
  for ( int i = 1; i < n; i++) //依次对其余n-1个顶点进行计算
  {
  int min = MAX;
  int v = v0;
  for ( int w = 0; w < n; w++)
  {
   if (!S[w] && D[w] < min)
   { //选择一条当前最短路径，终点为v
   v = w;
   min = D[w];
   }
   S[v] = true ; //将v加到s集合中
   for ( int w = 0; w < n; w++)
   { //更新从v0出发到集合V-S上所有顶点的最短路径长度
   if (!S[w] && (D[v] + G.arcs[v][w] < D[w]))
   {
    D[w] = D[v] + G.arcs[v][w]; //更新D[w]
    Path[w] = v; //更改w的前驱为v
   }
   }
  }
  }
}
//背景函数
void backGround()
{
  cout << "|*****************************************************************|" << endl;
  cout << " |------------------------铁大旅游景点图-----------------|" << endl;
  cout << "|*****************************************************************|" << endl;
  cout << "|  ⑦      单位：米 |" << endl;
  cout << "|  九教       |" << endl;
  cout << "|  ◎     ⑧  |" << endl;
  cout << "|  ↗↖     九栋  |" << endl;
  cout << "| ③ 200╱ ╲     ◎  |" << endl;
  cout << "| 西 ↙ ╲ 150    ↗ ↖  |" << endl;
  cout << "| 操 ◎  ╲ ①  160 ╱ ╲ 200 |" << endl;
  cout << "| 场 ↖150  ╲ 信息  ⑥ ╱  ╲ |" << endl;
  cout << "| ④ ↘ 140 ↘ 学院 200 基教 ↙ 230 ↘ |" << endl;
  cout << "| 体育馆 ◎-------------→◎←--------------→◎←--------------→◎ |" << endl;
  cout << "|  ↖  ↗ ↖  ↗ ↖  ↗② |" << endl;
  cout << "|  100 ╲ ╱ ╲ 125 ╱ ╲ 150 ╱ 综 |" << endl;
  cout << "|  ↘ ↙ 100 ╲ ╱135 ╲ ╱145 餐 |" << endl;
  cout << "|   ◎  ↘ ↙  ↘ ↙ |" << endl;
  cout << "|  ⑨ 沁园  ◎   ◎  |" << endl;
  cout << "|    ⑩ 翠园  ⑤ 春晖楼  |" << endl;
  cout << "|        |" << endl;
  cout << "|*****************************************************************|" << endl;
 
}
//主菜单
void menu()
{
  cout << "|*****************************************************************|" << endl;
  cout << "|----------------------------铁大导游小程序-----------------------|" << endl;
  cout << " |*********************************************************|" << endl;
  cout << " |--------------------1-景点信息查询--------------|" << endl;
  cout << " |--------------------2-最短路径查询--------------|" << endl;
  cout << " |--------------------3-显示景点视图--------------|" << endl;
  cout << " |-------------------4-退出导游程序------ --------|" << endl;
  cout << "|*****************************************************************|" << endl;
  cout << ">>>请选择：" ;
}
//景点信息查询二级菜单
void jmenu()
{
  cout << "|*****************************************************************|" << endl;
  cout << " |-------------------------景点信息查询------------------------|" << endl;
  cout << " |***********************************************************|" << endl;
  cout << " |----------------------1-信息学院介绍-------------------| " << endl;
  cout << " |----------------------2-综合餐厅介绍-------------------| " << endl;
  cout << " |----------------------3-西操场介绍---------------------| " << endl;
  cout << " |----------------------4-体育馆介绍---------------------| " << endl;
  cout << " |----------------------5-春晖楼介绍---------------------| " << endl;
  cout << " |----------------------6-基教介绍-----------------------| " << endl;
  cout << " |----------------------7-九教介绍-----------------------| " << endl;
  cout << " |----------------------8-九栋介绍-----------------------| " << endl;
  cout << " |----------------------9-沁园介绍-----------------------| " << endl;
  cout << " |---------------------10-翠园介绍-----------------------| " << endl;
  cout << "|*****************************************************************|" << endl;
  cout << ">>>请要查询的景点编号：" ;
}
//最短路径查询二级菜单
void pmenu()
{
  cout << "|*****************************************************************|" << endl;
  cout << " |-------------------------最短路径查询------------------------|" << endl;
  cout << " |***********************************************************|" << endl;
  cout << " |---------------------1-信息学院-------------------| " << endl;
  cout << " | --------------------2-综合餐厅-------------------| " << endl;
  cout << " |---------------------3-西操场---------------------| " << endl;
  cout << " |---------------------4-体育馆---------------------| " << endl;
  cout << " |---------------------5-春晖楼---------------------| " << endl;
  cout << " |---------------------6-基教-----------------------| " << endl;
  cout << " |---------------------7-九教-----------------------| " << endl;
  cout << " |---------------------8-九栋-----------------------| " << endl;
  cout << " |---------------------9-沁园-----------------------| " << endl;
  cout << " |--------------------10-翠园-----------------------| " << endl;
  cout << "|*****************************************************************|" << endl;
  cout << ">>>请依次输入起点编号和终点编号：" ;
}
void main()
{
  //初始化操作
  AMGraph amg = { { "信息学院" , "综合餐厅" , "西操场" , "体育馆" , "春晖楼" ,
    "基教" , "九教" , "九栋" , "沁园" , "翠园" },
  //-1代表两边不相连，权值无限大
  //邻接矩阵 /* 信 综 西 体 春 基 教 栋 沁 翠*/
    {{MAX,MAX,MAX,140,MAX,200,150,MAX,100,125 },
    {MAX,MAX,MAX,MAX,145,230,MAX,100,MAX,MAX },
    {MAX,MAX,MAX,150,MAX,MAX,200,MAX,MAX,MAX },
    {140,MAX,150,MAX,MAX,MAX,MAX,MAX,100,MAX },
    {MAX,145,MAX,MAX,MAX,150,MAX,MAX,MAX,MAX },
    {200,230,MAX,MAX,150,MAX,MAX,160,MAX,135 },
    {150,MAX,200,MAX,MAX,MAX,MAX,MAX,MAX,MAX },
    {MAX,200,MAX,MAX,MAX,160,MAX,MAX,MAX,MAX },
    {100,MAX,MAX,100,MAX,MAX,MAX,MAX,MAX,MAX },
    {125,MAX,MAX,MAX,MAX,135,MAX,MAX,MAX,MAX }
    },10,14};
  int f, ff;
  int start, end;
  while ( true )
  {
  cout << endl;
  menu();
  cin >> f;
  if (f == 1)
  {
   jmenu();
   cin >> ff;
　　　　　　　 //景点信息从文件中读取
   ifstream outfile( "schooltravel.txt" , ios :: out | ios :: binary);
   if (!outfile)
   {
   cerr << "读取景点介绍文件失败！" << endl;
   abort ();
   }
   string str[max];
   int i = 0;
   while (getline(outfile, str[i++]));
   cout << "|-----------------------景点介绍-------------------| " << endl;
   if (ff == 1)
   cout << str[0] << endl;
   else if (ff == 2)
   cout << str[1] << endl;
   else if (ff == 3)
   cout << str[2] << endl;
   else if (ff == 4)
   cout << str[3] << endl;
   else if (ff == 5)
   cout << str[4] << endl;
   else if (ff == 6)
   cout << str[5] << endl;
   else if (ff == 7)
   cout << str[6] << endl;
   else if (ff == 8)
   cout << str[7] << endl;
   else if (ff == 9)
   cout << str[8] << endl;
   else if (ff == 10)
   cout << str[9] << endl;
   cout << "|-------------------------------------------------|" << endl;
  }
  else if (f == 2)
  {
   pmenu();
   cin >> start >> end;
   ShortestPath_DIJ(amg, start - 1);
   int temp = end-1;
   int temp1, temp2;
   int flag[max], m = 0;
   cout << "从" << amg.vexs[start - 1] << "到" << amg.vexs[end - 1] << "最短路径为：" ;
   while (temp!= -1)
   {
   flag[m++] = temp;
   temp1 = temp ;
   temp2 = Path[temp1];
   temp = temp2;
   }
   for ( int i = m-1; i >= 0; i--)
   {
   cout <<amg.vexs[flag[i]] << "->" ;
   }
   cout << endl;
   cout << "最短路径值为：" << D[end - 1] << "米" << endl;
  }
  else if (f == 3)
  {
   backGround();
  }
  else if (f == 4)
  {
   cout << ">>>退出成功！" << endl;
   exit (0);
  }
  }
}

（4）运行截图:

C++用Dijkstra(迪杰斯特拉)算法求最短路径

C++用Dijkstra(迪杰斯特拉)算法求最短路径

C++用Dijkstra(迪杰斯特拉)算法求最短路径

总结 。

以上就是关于C++用Dijkstra算法(迪杰斯特拉算法)求最短路径的全部内容了，希望本文的内容对大家的学习或者工作带来一定的帮助，如果有疑问大家可以留言交流.

最后此篇关于C++用Dijkstra(迪杰斯特拉)算法求最短路径的文章就讲到这里了,如果你想了解更多关于C++用Dijkstra(迪杰斯特拉)算法求最短路径的内容请搜索CFSDN的文章或继续浏览相关文章，希望大家以后支持我的博客！ 。

28 4 0
文章推荐： 正则表达式初运用之认证界面的实现代码
文章推荐： C++时间戳转换成日期时间的步骤和示例代码
文章推荐： Javascript校验密码复杂度的正则表达式
文章推荐： Javascript使用正则验证身份证号(简单)
qq735679552
个人简介

我是一名优秀的程序员,十分优秀！

滴滴打车优惠券免费领取
滴滴打车优惠券
全站热门文章
Copyright 2021 - 2024 cfsdn All Rights Reserved 蜀ICP备2022000587号
广告合作:1813099741@qq.com 6ren.com