个人中心
gpt4 book ai didi

Java实现二叉树的深度优先遍历和广度优先遍历算法示例

转载 作者：qq735679552 更新时间：2022-09-27 22:32:09 27 4
gpt4 key购买 nike

CFSDN坚持开源创造价值，我们致力于搭建一个资源共享平台，让每一个IT人在这里找到属于你的精彩世界.

这篇CFSDN的博客文章Java实现二叉树的深度优先遍历和广度优先遍历算法示例由作者收集整理，如果你对这篇文章有兴趣，记得点赞哟.

本文实例讲述了java实现二叉树的深度优先遍历和广度优先遍历算法。分享给大家供大家参考，具体如下:

1. 分析 。

二叉树的深度优先遍历的非递归的通用做法是采用栈，广度优先遍历的非递归的通用做法是采用队列.

深度优先遍历：对每一个可能的分支路径深入到不能再深入为止，而且每个结点只能访问一次。要特别注意的是，二叉树的深度优先遍历比较特殊，可以细分为先序遍历、中序遍历、后序遍历。具体说明如下:

先序遍历：对任一子树，先访问根，然后遍历其左子树，最后遍历其右子树.

中序遍历：对任一子树，先遍历其左子树，然后访问根，最后遍历其右子树.

后序遍历：对任一子树，先遍历其左子树，然后遍历其右子树，最后访问根.

广度优先遍历：又叫层次遍历，从上往下对每一层依次访问，在每一层中，从左往右（也可以从右往左）访问结点，访问完一层就进入下一层，直到没有结点可以访问为止.

2. 举例说明 。

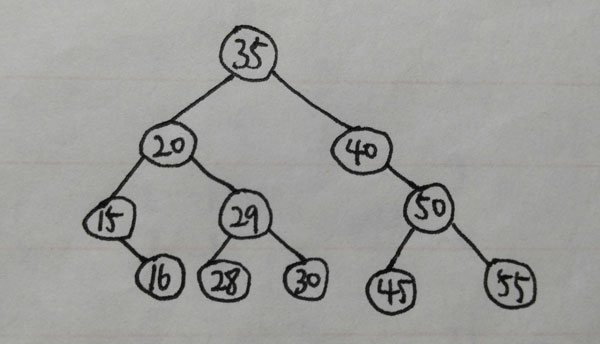
对下图所示的二叉排序树进行遍历，要求使用先序遍历（递归、非递归）、中序遍历（递归、非递归）、后序遍历（递归、非递归）和广度优先遍历.

Java实现二叉树的深度优先遍历和广度优先遍历算法示例

① 参考代码 。

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
package binarytreetraversetest;
import java.util.linkedlist;
import java.util.queue;
/**
  * 二叉树的深度优先遍历和广度优先遍历
  * @author fantasy
  * @version 1.0 2016/10/05 - 2016/10/07
  */
public class binarytreetraversetest {
   public static void main(string[] args) {
   binarysorttree<integer> tree = new binarysorttree<integer>();
     tree.insertnode( 35 );
     tree.insertnode( 20 );
     tree.insertnode( 15 );
     tree.insertnode( 16 );
     tree.insertnode( 29 );
     tree.insertnode( 28 );
     tree.insertnode( 30 );
     tree.insertnode( 40 );
     tree.insertnode( 50 );
     tree.insertnode( 45 );
     tree.insertnode( 55 );
     system.out.print( "先序遍历（递归）：" );
     tree.preordertraverse(tree.getroot());
     system.out.println();
     system.out.print( "中序遍历（递归）：" );
     tree.inordertraverse(tree.getroot());
     system.out.println();
     system.out.print( "后序遍历（递归）：" );
     tree.postordertraverse(tree.getroot());
     system.out.println();
     system.out.print( "先序遍历（非递归）：" );
     tree.preordertraversenorecursion(tree.getroot());
     system.out.println();
     system.out.print( "中序遍历（非递归）：" );
     tree.inordertraversenorecursion(tree.getroot());
     system.out.println();
     system.out.print( "后序遍历（非递归）：" );
     tree.postordertraversenorecursion(tree.getroot());
     system.out.println();
     system.out.print( "广度优先遍历：" );
     tree.breadthfirsttraverse(tree.getroot());
   }
}
/**
  * 结点
  */
class node<e extends comparable<e>> {
   e value;
   node<e> left;
   node<e> right;
   node(e value) {
     this .value = value;
     left = null ;
     right = null ;
   }
}
/**
  * 使用一个先序序列构建一棵二叉排序树（又称二叉查找树）
  */
class binarysorttree<e extends comparable<e>> {
   private node<e> root;
   binarysorttree() {
     root = null ;
   }
   public void insertnode(e value) {
     if (root == null ) {
       root = new node<e>(value);
       return ;
     }
     node<e> currentnode = root;
     while ( true ) {
       if (value.compareto(currentnode.value) > 0 ) {
         if (currentnode.right == null ) {
           currentnode.right = new node<e>(value);
           break ;
         }
         currentnode = currentnode.right;
       } else {
         if (currentnode.left == null ) {
           currentnode.left = new node<e>(value);
           break ;
         }
         currentnode = currentnode.left;
       }
     }
   }
   public node<e> getroot(){
     return root;
   }
   /**
    * 先序遍历二叉树（递归）
    * @param node
    */
   public void preordertraverse(node<e> node) {
     system.out.print(node.value + " " );
     if (node.left != null )
       preordertraverse(node.left);
     if (node.right != null )
       preordertraverse(node.right);
   }
   /**
    * 中序遍历二叉树（递归）
    * @param node
    */
   public void inordertraverse(node<e> node) {
     if (node.left != null )
       inordertraverse(node.left);
     system.out.print(node.value + " " );
     if (node.right != null )
       inordertraverse(node.right);
   }
   /**
    * 后序遍历二叉树（递归）
    * @param node
    */
   public void postordertraverse(node<e> node) {
     if (node.left != null )
       postordertraverse(node.left);
     if (node.right != null )
       postordertraverse(node.right);
     system.out.print(node.value + " " );
   }
   /**
    * 先序遍历二叉树（非递归）
    * @param root
    */
   public void preordertraversenorecursion(node<e> root) {
     linkedlist<node<e>> stack = new linkedlist<node<e>>();
     node<e> currentnode = null ;
     stack.push(root);
     while (!stack.isempty()) {
       currentnode = stack.pop();
       system.out.print(currentnode.value + " " );
       if (currentnode.right != null )
         stack.push(currentnode.right);
       if (currentnode.left != null )
         stack.push(currentnode.left);
     }
   }
   /**
    * 中序遍历二叉树（非递归）
    * @param root
    */
   public void inordertraversenorecursion(node<e> root) {
     linkedlist<node<e>> stack = new linkedlist<node<e>>();
     node<e> currentnode = root;
     while (currentnode != null || !stack.isempty()) {
       // 一直循环到二叉排序树最左端的叶子结点（currentnode是null）
       while (currentnode != null ) {
         stack.push(currentnode);
         currentnode = currentnode.left;
       }
       currentnode = stack.pop();
       system.out.print(currentnode.value + " " );
       currentnode = currentnode.right;
     }
   }
   /**
    * 后序遍历二叉树（非递归）
    * @param root
    */
   public void postordertraversenorecursion(node<e> root) {
     linkedlist<node<e>> stack = new linkedlist<node<e>>();
     node<e> currentnode = root;
     node<e> rightnode = null ;
     while (currentnode != null || !stack.isempty()) {
       // 一直循环到二叉排序树最左端的叶子结点（currentnode是null）
       while (currentnode != null ) {
         stack.push(currentnode);
         currentnode = currentnode.left;
       }
       currentnode = stack.pop();
       // 当前结点没有右结点或上一个结点（已经输出的结点）是当前结点的右结点，则输出当前结点
       while (currentnode.right == null || currentnode.right == rightnode) {
         system.out.print(currentnode.value + " " );
         rightnode = currentnode;
         if (stack.isempty()) {
           return ; //root以输出，则遍历结束
         }
         currentnode = stack.pop();
       }
       stack.push(currentnode); //还有右结点没有遍历
       currentnode = currentnode.right;
     }
   }
   /**
    * 广度优先遍历二叉树，又称层次遍历二叉树
    * @param node
    */
   public void breadthfirsttraverse(node<e> root) {
     queue<node<e>> queue = new linkedlist<node<e>>();
     node<e> currentnode = null ;
     queue.offer(root);
     while (!queue.isempty()) {
       currentnode = queue.poll();
       system.out.print(currentnode.value + " " );
       if (currentnode.left != null )
         queue.offer(currentnode.left);
       if (currentnode.right != null )
         queue.offer(currentnode.right);
     }
   }
}

② 输出结果 。

先序遍历（递归）：35 20 15 16 29 28 30 40 50 45 55 中序遍历（递归）：15 16 20 28 29 30 35 40 45 50 55 后序遍历（递归）：16 15 28 30 29 20 45 55 50 40 35 先序遍历（非递归）：35 20 15 16 29 28 30 40 50 45 55 中序遍历（非递归）：15 16 20 28 29 30 35 40 45 50 55 后序遍历（非递归）：16 15 28 30 29 20 45 55 50 40 35 广度优先遍历：35 20 40 15 29 50 16 28 30 45 55 。

希望本文所述对大家java程序设计有所帮助.

原文链接：https://blog.csdn.net/fantasy_lin_/article/details/52751559 。

最后此篇关于Java实现二叉树的深度优先遍历和广度优先遍历算法示例的文章就讲到这里了,如果你想了解更多关于Java实现二叉树的深度优先遍历和广度优先遍历算法示例的内容请搜索CFSDN的文章或继续浏览相关文章，希望大家以后支持我的博客！ 。

27 4 0
文章推荐： PHP+jquery+ajax实现即时聊天功能实例
文章推荐： PHP采集静态页面并把页面css,img,js保存的方法
文章推荐： 微信公众平台消息接口校验与消息接口响应实例
文章推荐： php获取QQ头像并显示的方法
qq735679552
个人简介

我是一名优秀的程序员,十分优秀！

滴滴打车优惠券免费领取
滴滴打车优惠券
全站热门文章
Copyright 2021 - 2024 cfsdn All Rights Reserved 蜀ICP备2022000587号
广告合作:1813099741@qq.com 6ren.com