个人中心
gpt4 book ai didi

神经网络(BP)算法Python实现及应用

转载 作者：qq735679552 更新时间：2022-09-28 22:32:09 30 4
gpt4 key购买 nike

CFSDN坚持开源创造价值，我们致力于搭建一个资源共享平台，让每一个IT人在这里找到属于你的精彩世界.

这篇CFSDN的博客文章神经网络(BP)算法Python实现及应用由作者收集整理，如果你对这篇文章有兴趣，记得点赞哟.

本文实例为大家分享了python实现神经网络算法及应用的具体代码，供大家参考，具体内容如下 。

首先用python实现简单地神经网络算法:

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
import numpy as np
 
 
# 定义tanh函数
def tanh(x):
   return np.tanh(x)
 
 
# tanh函数的导数
def tan_deriv(x):
   return 1.0 - np.tanh(x) * np.tan(x)
 
 
# sigmoid函数
def logistic(x):
   return 1 / ( 1 + np.exp( - x))
 
 
# sigmoid函数的导数
def logistic_derivative(x):
   return logistic(x) * ( 1 - logistic(x))
 
 
class neuralnetwork:
   def __init__( self , layers, activation = 'tanh' ):
     """
     神经网络算法构造函数
     :param layers: 神经元层数
     :param activation: 使用的函数（默认tanh函数）
     :return:none
     """
     if activation = = 'logistic' :
       self .activation = logistic
       self .activation_deriv = logistic_derivative
     elif activation = = 'tanh' :
       self .activation = tanh
       self .activation_deriv = tan_deriv
 
     # 权重列表
     self .weights = []
     # 初始化权重（随机）
     for i in range ( 1 , len (layers) - 1 ):
       self .weights.append(( 2 * np.random.random((layers[i - 1 ] + 1 , layers[i] + 1 )) - 1 ) * 0.25 )
       self .weights.append(( 2 * np.random.random((layers[i] + 1 , layers[i + 1 ])) - 1 ) * 0.25 )
 
   def fit( self , x, y, learning_rate = 0.2 , epochs = 10000 ):
     """
     训练神经网络
     :param x: 数据集（通常是二维）
     :param y: 分类标记
     :param learning_rate: 学习率（默认0.2）
     :param epochs: 训练次数（最大循环次数，默认10000）
     :return: none
     """
     # 确保数据集是二维的
     x = np.atleast_2d(x)
 
     temp = np.ones([x.shape[ 0 ], x.shape[ 1 ] + 1 ])
     temp[:, 0 : - 1 ] = x
     x = temp
     y = np.array(y)
 
     for k in range (epochs):
       # 随机抽取x的一行
       i = np.random.randint(x.shape[ 0 ])
       # 用随机抽取的这一组数据对神经网络更新
       a = [x[i]]
       # 正向更新
       for l in range ( len ( self .weights)):
         a.append( self .activation(np.dot(a[l], self .weights[l])))
       error = y[i] - a[ - 1 ]
       deltas = [error * self .activation_deriv(a[ - 1 ])]
 
       # 反向更新
       for l in range ( len (a) - 2 , 0 , - 1 ):
         deltas.append(deltas[ - 1 ].dot( self .weights[l].t) * self .activation_deriv(a[l]))
         deltas.reverse()
       for i in range ( len ( self .weights)):
         layer = np.atleast_2d(a[i])
         delta = np.atleast_2d(deltas[i])
         self .weights[i] + = learning_rate * layer.t.dot(delta)
 
   def predict( self , x):
     x = np.array(x)
     temp = np.ones(x.shape[ 0 ] + 1 )
     temp[ 0 : - 1 ] = x
     a = temp
     for l in range ( 0 , len ( self .weights)):
       a = self .activation(np.dot(a, self .weights[l]))
     return a

使用自己定义的神经网络算法实现一些简单的功能:

 小案例:

x:                  y 0 0                 0 0 1                 1 1 0                 1 1 1                 0 。

?
1
2
3
4
5
6
7
8
9
10
from nn.neuralnetwork import neuralnetwork
import numpy as np
 
nn = neuralnetwork([ 2 , 2 , 1 ], 'tanh' )
temp = [[ 0 , 0 ], [ 0 , 1 ], [ 1 , 0 ], [ 1 , 1 ]]
x = np.array(temp)
y = np.array([ 0 , 1 , 1 , 0 ])
nn.fit(x, y)
for i in temp:
   print (i, nn.predict(i))

神经网络(BP)算法Python实现及应用

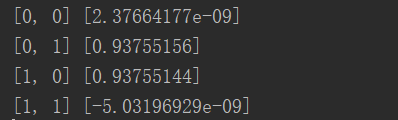
发现结果基本机制，无限接近0或者无限接近1  。

第二个例子：识别图片中的数字 。

导入数据:

?
1
2
3
4
5
6
7
8
from sklearn.datasets import load_digits
import pylab as pl
 
digits = load_digits()
print (digits.data.shape)
pl.gray()
pl.matshow(digits.images[ 0 ])
pl.show()

观察下：大小：(1797, 64) 。

数字0 。

神经网络(BP)算法Python实现及应用

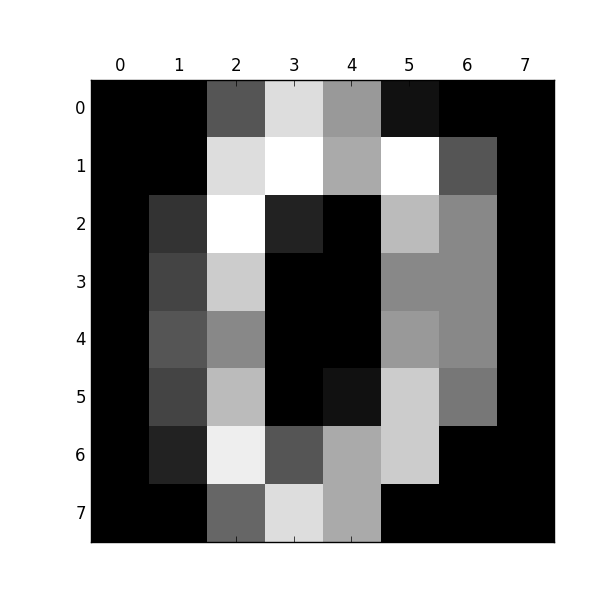
接下来的代码是识别它们:

?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
import numpy as np
from sklearn.datasets import load_digits
from sklearn.metrics import confusion_matrix, classification_report
from sklearn.preprocessing import labelbinarizer
from nn.neuralnetwork import neuralnetwork
from sklearn.cross_validation import train_test_split
 
# 加载数据集
digits = load_digits()
x = digits.data
y = digits.target
# 处理数据，使得数据处于0,1之间，满足神经网络算法的要求
x - = x. min ()
x / = x. max ()
 
# 层数：
# 输出层10个数字
# 输入层64因为图片是8*8的，64像素
# 隐藏层假设100
nn = neuralnetwork([ 64 , 100 , 10 ], 'logistic' )
# 分隔训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(x, y)
 
# 转化成sklearn需要的二维数据类型
labels_train = labelbinarizer().fit_transform(y_train)
labels_test = labelbinarizer().fit_transform(y_test)
print ( "start fitting" )
# 训练3000次
nn.fit(x_train, labels_train, epochs = 3000 )
predictions = []
for i in range (x_test.shape[ 0 ]):
   o = nn.predict(x_test[i])
   # np.argmax:第几个数对应最大概率值
   predictions.append(np.argmax(o))
 
# 打印预测相关信息
print (confusion_matrix(y_test, predictions))
print (classification_report(y_test, predictions))

结果:

矩阵对角线代表预测正确的数量，发现正确率很多 。

神经网络(BP)算法Python实现及应用

  。

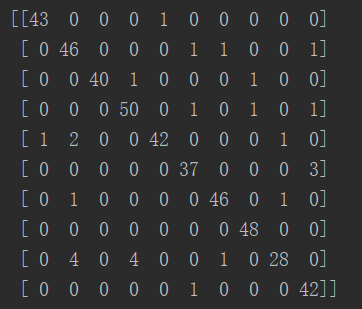
这张表更直观地显示出预测正确率:

共450个案例，成功率94% 。

神经网络(BP)算法Python实现及应用

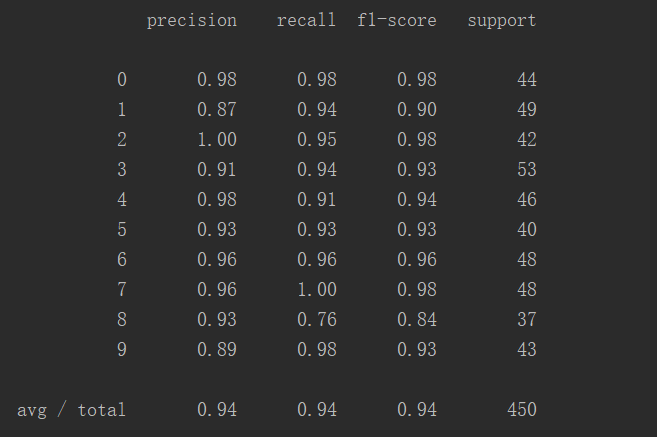
以上就是本文的全部内容，希望对大家的学习有所帮助，也希望大家多多支持我.

原文链接：http://www.cnblogs.com/xuyiqing/p/8797048.html 。

最后此篇关于神经网络(BP)算法Python实现及应用的文章就讲到这里了,如果你想了解更多关于神经网络(BP)算法Python实现及应用的内容请搜索CFSDN的文章或继续浏览相关文章，希望大家以后支持我的博客！ 。

30 4 0
文章推荐： Python中list列表的一些进阶使用方法介绍
文章推荐： Android解析Intent Filter的方法
文章推荐： Python中的super()方法使用简介
文章推荐： android创建optionsmenu的方法
qq735679552
个人简介

我是一名优秀的程序员,十分优秀！

滴滴打车优惠券免费领取
滴滴打车优惠券
Copyright 2021 - 2024 cfsdn All Rights Reserved 蜀ICP备2022000587号
广告合作:1813099741@qq.com 6ren.com