CFSDN坚持开源创造价值，我们致力于搭建一个资源共享平台，让每一个IT人在这里找到属于你的精彩世界.

这篇CFSDN的博客文章C语言实现字符串匹配KMP算法由作者收集整理，如果你对这篇文章有兴趣，记得点赞哟.

字符串匹配是计算机的基本任务之一.

举例来说，有一个字符串"BBC ABCDAB ABCDABCDABDE"，我想知道，里面是否包含另一个字符串"ABCDABD"?

下面的的KMP算法的解释步骤 。

1. 。

首先，字符串"BBC ABCDAB ABCDABCDABDE"的第一个字符与搜索词"ABCDABD"的第一个字符，进行比较。因为B与A不匹配，所以搜索词后移一位.

2. 。

因为B与A不匹配，搜索词再往后移.

3. 。

就这样，直到字符串有一个字符，与搜索词的第一个字符相同为止.

4. 。

接着比较字符串和搜索词的下一个字符，还是相同.

5. 。

直到字符串有一个字符，与搜索词对应的字符不相同为止.

6. 。

这时，最自然的反应是，将搜索词整个后移一位，再从头逐个比较。这样做虽然可行，但是效率很差，因为你要把"搜索位置"移到已经比较过的位置，重比一遍.

7. 。

一个基本事实是，当空格与D不匹配时，你其实知道前面六个字符是"ABCDAB"。KMP算法的想法是，设法利用这个已知信息，不要把"搜索位置"移回已经比较过的位置，继续把它向后移，这样就提高了效率.

8. 。

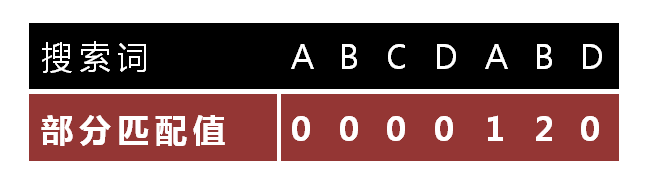
怎么做到这一点呢？可以针对搜索词，算出一张《部分匹配表》（Partial Match Table）。这张表是如何产生的，后面再介绍，这里只要会用就可以了.

9. 。

已知空格与D不匹配时，前面六个字符"ABCDAB"是匹配的。查表可知，最后一个匹配字符B对应的"部分匹配值"为2，因此按照下面的公式算出向后移动的位数:

　　移动位数 = 已匹配的字符数 - 对应的部分匹配值 。

因为 6 - 2 等于4，所以将搜索词向后移动4位.

10. 。

因为空格与Ｃ不匹配，搜索词还要继续往后移。这时，已匹配的字符数为2（"AB"），对应的"部分匹配值"为0。所以，移动位数 = 2 - 0，结果为 2，于是将搜索词向后移2位.

11. 。

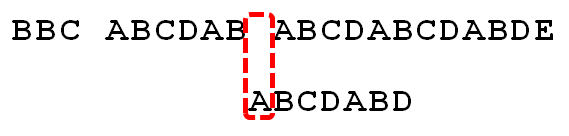
因为空格与A不匹配，继续后移一位.

12. 。

逐位比较，直到发现C与D不匹配。于是，移动位数 = 6 - 2，继续将搜索词向后移动4位.

13. 。

逐位比较，直到搜索词的最后一位，发现完全匹配，于是搜索完成。如果还要继续搜索（即找出全部匹配），移动位数 = 7 - 0，再将搜索词向后移动7位，这里就不再重复了.

14. 。

下面介绍《部分匹配表》是如何产生的.

首先，要了解两个概念："前缀"和"后缀"。 "前缀"指除了最后一个字符以外，一个字符串的全部头部组合；"后缀"指除了第一个字符以外，一个字符串的全部尾部组合.

15. 。

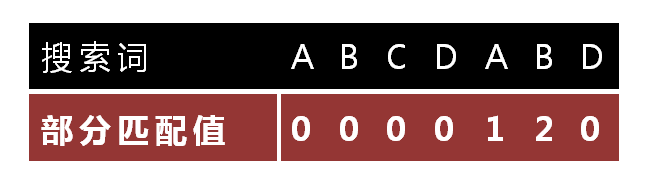
"部分匹配值"就是"前缀"和"后缀"的最长的共有元素的长度。以"ABCDABD"为例， 。

　　－　"A"的前缀和后缀都为空集，共有元素的长度为0； 。

　　－　"AB"的前缀为[A]，后缀为[B]，共有元素的长度为0； 。

　　－　"ABC"的前缀为[A, AB]，后缀为[BC, C]，共有元素的长度0； 。

　　－　"ABCD"的前缀为[A, AB, ABC]，后缀为[BCD, CD, D]，共有元素的长度为0； 。

　　－　"ABCDA"的前缀为[A, AB, ABC, ABCD]，后缀为[BCDA, CDA, DA, A]，共有元素为"A"，长度为1； 。

　　－　"ABCDAB"的前缀为[A, AB, ABC, ABCD, ABCDA]，后缀为[BCDAB, CDAB, DAB, AB, B]，共有元素为"AB"，长度为2； 。

　　－　"ABCDABD"的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB]，后缀为[BCDABD, CDABD, DABD, ABD, BD, D]，共有元素的长度为0.

16. 。

"部分匹配"的实质是，有时候，字符串头部和尾部会有重复。比如，"ABCDAB"之中有两个"AB"，那么它的"部分匹配值"就是2（"AB"的长度）。搜索词移动的时候，第一个"AB"向后移动4位（字符串长度-部分匹配值），就可以来到第二个"AB"的位置.

  。

　　接下来，就是我自己对KMP算法的实现了.

　　这个算法的实现主要包括了三个方面:

　　1) 求得我们用来搜索字符串的部分匹配值表 。

　　2) 实现待搜索字符串在搜索过程中的指针的移动问题 。

　　3) 如何定位我们搜索到的结果 。

　　接下来我就贴上我实现的代码 。

　　

/**用KMP算法实现字符串匹配搜索方法*该程序实现的功能是搜索本目录下的所有文件的内容是否与给定的*字符串匹配，如果匹配，则输出文件名：包含该字符串的行*待搜索的目标串搜索指针移动位数 = 已匹配的字符数 - 对应部分匹配值*/

#include <stdio.h>#include <string.h>#include <stdlib.h>

#define KEYWORD_MAX_LENGTH 100      //设定搜索串的最大长度

int kmp_table[KEYWORD_MAX_LENGTH];  //为搜索串建立kmp表char prefix_stack[KEYWORD_MAX_LENGTH]; //前缀表达式栈char suffix_stack[KEYWORD_MAX_LENGTH]; //后缀表达式栈int keyword_length = 0;  //搜索串的长度int record_position[KEYWORD_MAX_LENGTH]; //记录与关键字串匹配源串中的位置

/**GetMatchValue:获得字符串src的部分匹配值*/int GetMatchValue(char *src){    int value = 0;    int src_len = strlen(src);    char *begin = src;    //初始化指向字符串第一个字符    char *end = src + (src_len - 1);  //初始化指向字符串最后一个字符    int i = 0;    for(i=0;i<(src_len-1);i++)    {        prefix_stack[i] = *begin;        suffix_stack[i] = *end;        begin++;        end--;    }    char *p = prefix_stack;    char *q = suffix_stack + (src_len - 2);  //指向栈中最后一个元素    int flag = 0;   //用一个标志位来确定后缀栈中到最后一个元素都与前缀栈中的符号匹配    while(q >= suffix_stack)    {        if(*p == *q)        {            value++;            p++;            flag=1;        }        else {            flag = 0;        }        q--;    }    if(flag == 0) value = 0;    return value;}

/**创建搜索字符串的KMP表*/int Create_KMP_Table(char *str,int *table){    int i;    char *dst;    keyword_length = strlen(str);    for(i=0;i<keyword_length;i++)    {        if(i == 0) {            table[i] = 0;   //第一个字符无前缀和后缀，所以为0        }        else {            dst = (char*)malloc((i+2));            if(dst == NULL)            {                printf("malloc space error!\n");                return EXIT_FAILURE;            }            strncpy(dst,str,(i+1));   //匹配str的前(i+1)个字符            dst[i+1] = '\0';    //注意字符串要以'/0'结尾            table[i] = GetMatchValue(dst);             free((void*)dst);            }    }    return EXIT_SUCCESS;}

//打印搜索字符串对应的KMP表void Table_Print(char *str,int *table){    int i;    char c = *str;    while(c != '\0')    {        printf("%-4c",c);        //左对齐输出搜索字符串中的字符        c = *++str;    }    printf("\n");    for(i=0;i<keyword_length;i++)    {        printf("%-4d",table[i]); //左对齐输出每个字符对应的部分匹配值    }    printf("\n");}

//在目标串dst_str中搜索关键子串search_str,打印出关键字串的位置信息,返回与关键字串匹配的数目int Search_Keyword(char *dst_str,char *search_str){    char *p = dst_str;    char *q = search_str;    char *temp;

    //创建关键字串的KMP表        Create_KMP_Table(search_str,kmp_table);        int count = 0;  //记录现在已经匹配的数目    int k = 0;     //记录与关键字串匹配的字串的数目    int move = 0;  //当字符串不匹配时，搜索指针移动的位数    

    while(*p != '\0')   //直到搜索到目标串的最后一个字符为止    {        temp = p;        while(*q != '\0')        {            if(*q == *temp)            {                count++;                temp++;                q++;            }            else break;        }                if(count == 0)            p++;        else {            if(count == keyword_length)            {                record_position[k++] = (temp-dst_str)-(keyword_length);            }            move = count - kmp_table[count-1];            p += move;        }

        count = 0;        q = search_str;    }    return k;}

int main(int argc,char **argv){    char *search_str = argv[1];    //char dst_str[] = "hello woshijpf woshijpf woshij woshijp woshijpf";    char dst_str[] = "BBC ABCDAB ABCDABCDABDE";        printf("Please input serach string and dst_string\n");    if(search_str == NULL)    {        printf("Please input search string\n");        return EXIT_FAILURE;    }

    if(dst_str == NULL)    {        printf("Please input dst_string\n");        return EXIT_FAILURE;    }        int result = Search_Keyword(dst_str,search_str);  //放回搜索到的结果的数目    Table_Print(search_str,kmp_table);    printf("%s\n",dst_str);         //输出待搜索的目标串    if(result == 0)    {        printf("Sorry!Don't find the string %s\n",search_str);        return EXIT_SUCCESS;    }    else {        int i,j,num;        int before = 0;        for(i=0;i<result;i++)        {            num = record_position[i] - before;    //打印搜索串在目标串中的位置            before = record_position[i]+1;            for(j=1;j<=num;j++)                printf(" ");            printf("*");        }        printf("\n");    }        return EXIT_SUCCESS;}

  。

　　测试的结果:

　　

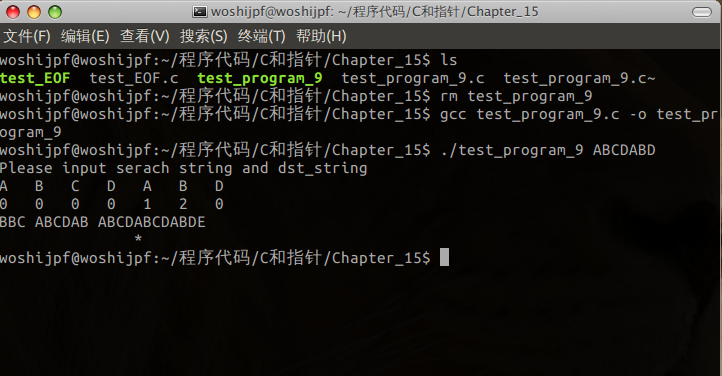
最后此篇关于C语言实现字符串匹配KMP算法的文章就讲到这里了,如果你想了解更多关于C语言实现字符串匹配KMP算法的内容请搜索CFSDN的文章或继续浏览相关文章，希望大家以后支持我的博客！ 。