- ubuntu12.04环境下使用kvm ioctl接口实现最简单的虚拟机
- Ubuntu 通过无线网络安装Ubuntu Server启动系统后连接无线网络的方法
- 在Ubuntu上搭建网桥的方法
- ubuntu 虚拟机上网方式及相关配置详解
CFSDN坚持开源创造价值,我们致力于搭建一个资源共享平台,让每一个IT人在这里找到属于你的精彩世界.
这篇CFSDN的博客文章mysql免安装版步骤解压后找不到密码处理方法由作者收集整理,如果你对这篇文章有兴趣,记得点赞哟.
1.解压mysql-8.0.21-winx64 2.配置环境变量,地址写到bin文件夹下 。
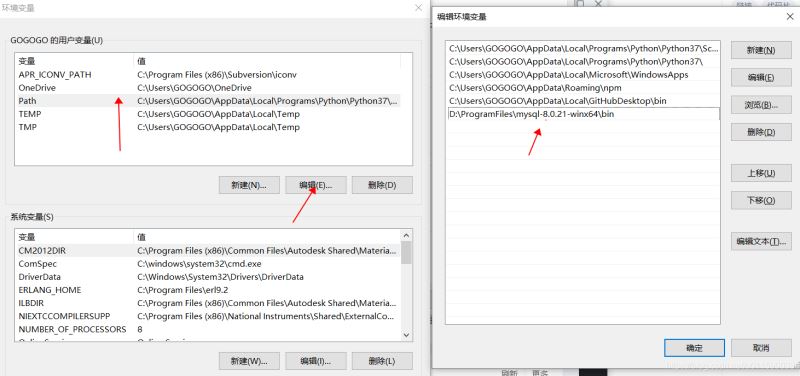
3.创建配置文件,命名为 my.ini,内容如下 。
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
[mysql]
# 设置mysql客户端默认字符集
default
-
character
-
set
=utf8
[mysqld]
interactive_timeout=28800000
wait_timeout=28800000
# 设置3306端口
port = 3306
# 设置mysql的安装目录
basedir=d:\programfiles\mysql-8.0.21-winx64\bin
# 设置mysql数据库的数据的存放目录
datadir=d:\programfiles\mysql-8.0.21-winx64\data
# 允许最大连接数
max_connections=200
# 设置mysql服务端默认字符集
character
-
set
-server=utf8
# 创建新表时将使用的默认存储引擎
default
-storage-engine=innodb
|
4.安装mysql服务,输入 。
|
1
|
mysqld –install
|

如果报以下错误,打开cmd.exe程序的时候选择“用管理员身份打开 。

5.初始化mysql,输入以下命令,mysql目录下会生成 data 文件夹 。
|
1
|
mysqld –-initialize
|
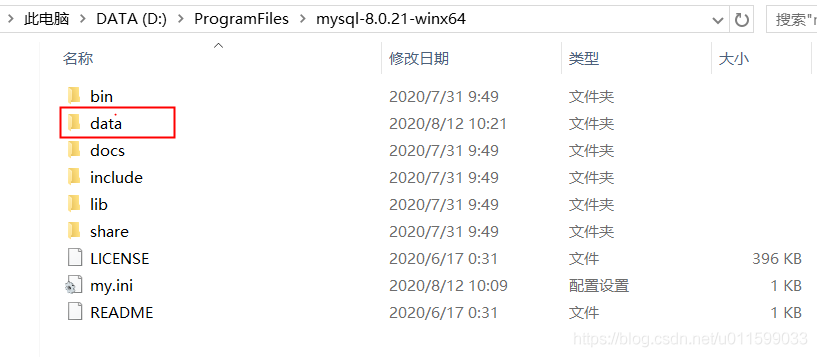
如果没有生成data文件夹,则使用以下命令 。
|
1
|
mysqld
--initialize-insecure --user=mysql
|
6.启动mysql,设置密码 。
|
1
2
|
net start mysql
mysql admin -u root -p
password
|

设置密码失败,百度一下,别人文档中有提到打开mysql根目录下的data文件夹,找到后缀是.err的文件以文本打开找到password临时密码(可以ctrl+f搜索)然后在cmd中输入该临时密码,但是我这里的.err文件中没有password,所以使用重置密码的方法 。
7.如果启动了mysql服务,就要停止mysql服务,使用命令 。
|
1
|
net stop mysql
|
8.使用mysqld –skip-grant-tables实测在mysql8.0.21中已失效,现使用以下命令进入免密登录模式 。
|
1
|
mysqld
--console --skip-grant-tables --shared-memory
|

9.另外开一个cmd窗口,使用mysql直接无密登录。输入以下命令回车,提示输入密码时再按回车进入 。
|
1
|
mysql -uroot -p
|
10.选择数据库,输入 。
|
1
|
use mysql
|

11.密码置空 。
|
1
|
update
user
set
authentication_string=
''
where
user
=‘root';
|
12.提示成功,一定要使用一下命令,再退出 。
|
1
2
|
flush
privileges
;
exit;
|
13.关闭免密登录模式的cmd窗口,启动mysql服务 。
|
1
|
net start mysql
|
14.步骤12密码已经置空,所以无密码状态登录mysql,输入登录命令:
|
1
|
mysql -u root -p
|
15.修改密码 。
|
1
|
alter
user
‘root
'@‘localhost'
identified
with
mysql_native_password
by
‘123456';
|
16.刷新权限后退出,大功告成 。
|
1
2
|
flush
privileges
;
exit;
|
到此这篇关于mysql免安装版步骤解压后找不到密码处理方法的文章就介绍到这了,更多相关mysql免安装版步骤内容请搜索我以前的文章或继续浏览下面的相关文章希望大家以后多多支持我! 。
原文链接:https://blog.csdn.net/u011599033/article/details/107941513 。
最后此篇关于mysql免安装版步骤解压后找不到密码处理方法的文章就讲到这里了,如果你想了解更多关于mysql免安装版步骤解压后找不到密码处理方法的内容请搜索CFSDN的文章或继续浏览相关文章,希望大家以后支持我的博客! 。
我希望通过扫描线为 x 的每个值找到 y 的值来绘制椭圆。 对于普通椭圆,公式很容易找到:y = Sqrt[b^2 - (b^2 x^2)/a^2] 但是当椭圆的轴旋转时,我一直无法弄清楚如何计算 y
假设我有这个矩阵: 1 1 1 | 1 0 0 1 | 1 这个系统显然有无限的解决方案。 x1 = -x2 x3 = 1 x1 依赖于 x2,x2 是免费的,但我感兴趣的是 x3。是否有一种算法可以
我正在考虑使用神经网络在我正在构建的太空射击游戏中为我的敌人提供动力,我想知道;当网络没有一个明确的好的输出集时,你如何训练神经网络? 最佳答案 我目前正在研究神经网络,如果没有明确定义的输入和输出编
我需要一个针对受限资源环境(例如具有以下特征的二进制(十六进制数据)嵌入式系统)进行优化的快速解压缩例程: 数据面向 8 位(字节)(数据总线为 8 位宽)。 字节值的范围并不统一为 0 - 0xFF
PHP代码: $txt="John has cat and dog."; //plain text $txt=base64_encode($txt); //base64 encode $txt=gzd
程序从用户那里接收到一个正数k,并且应该检查方程有多少解 3*x+5*y=k 在许多解决方案的情况下,该函数采用所有解决方案中 |x-y| 的较大绝对值。如果只有一种解决方案,它会打印出来。例如: 如
我必须求解以下微分方程: 或 如果没有 F_1 术语,代码就很简单。但我无法用包含 F_1 项来解决它,尽管我知道解决方案应该看起来像阻尼谐振。 from scipy.integrate import
我知道这个问题是前缀和的变体,我只是在设置它时遇到了一些困难。 最佳答案 定义: P[i] = A[i+1] + A[i+2] + ... + A[n] Q[i] = A[1] + ... + A[i
在许多在线示例中,文件在 Java 中使用编码缓冲区进行(解)压缩。然而,对于 NIO,无需选择一个好的缓冲区大小。我找到了文件和套接字的示例,但是是否有用于压缩输入的 NIO channel (例如
我有一个形式为 A*x = B 的方程组,其中 [A] 是一个三对角系数矩阵。使用 Numpy 求解器 numpy.linalg.solve 我可以求解 x 的方程组。 请参阅下面的示例,了解我如何开
我试图回答这个问题,只使用递归(动态编程) http://en.wikipedia.org/wiki/Longest_increasing_subsequence 从这篇文章中,我意识到最有效的现有解
解决此问题的方法是,按照我发帖的其中一项建议,将DLL添加到GAC中。正如我在我的一份答复中所指出的那样,在需要运行此过程的环境中,可伸缩性将不可用。因此,不能选择简单的解决方案。为了解决这个问题,我
是否有专门描述 AAC-LC 标准的规范,以及实现编解码器的现实目标,而不是通用编解码器,而是针对特定 AAC-LC 格式,具有预定义的 channel 数和采样率? 是否有一些针对 AAC-LC 的
我想使用通用的“p”来定义多路复用器将有多少输出。输入和所有输出均为 1 位。输出、控制和输入可以很简单,例如: signal control : std_logic_vector(log 2 p
我正在尝试在 javascript 中使用一些三 Angular 函数来定位一些菱形 div,但似乎我的逻辑在某处失败了。 你可以看到我尝试了这个公式:pos + trig * dimension。我
关闭。这个问题需要更多focused .它目前不接受答案。 想改进这个问题吗? 更新问题,使其只关注一个问题 editing this post . 关闭 4 年前。 Improve this qu
我一直在考虑这两个 JSON 库: 谷歌 Gson JSON.Simple XStream Google Gson 非常棒,它可以序列化具有无参数构造函数的类对象。 JSON.Simple 非常简洁,
使用 Gekko 拟合数据的数值 ODE 解。 嗨,大家好! 我想知道是否可以使用 GEKKO 拟合 ODE 的系数。 我尝试复制 example given here 失败. 这是我想出的(但有缺陷
众所周知,ASCII使用7位来编码字符,所以用来表示文本的字节数总是小于文本字母的长度 例如: StringBuilder text = new StringBuilder(); In
我找到了一个 link其中显示了一个示例,当线性方程组有无限多个解时,Matlab mldivide 运算符 (\) 给出“特殊”解。 例如: A = [1 2 0; 0 4 3]; b = [8;

我是一名优秀的程序员,十分优秀!