user-interface - 如何计算负加速度？

Question

我正在实现触摸屏 UI 的滚动行为，但我现在太累了，无法将我的思绪放在一些所谓的微不足道的数学上:

y (distance/velocity)
|********
|        ******
|              ****
|                  ***
|                     ***
|                        **
|                          **
|                            *
|                             *
-------------------------------- x (time)

f(x)->?

UI 应该允许用户在任何方向拖动和“抛出”一个 View ，并且即使在他从屏幕上松开手指后也能保持滚动一段时间。它的动量取决于用户在取下手指之前拖动的速度。

所以我有一个起始速度 (v0)，每 20 毫秒我滚动一个相对于当前速度的量。每次滚动迭代时，我都会稍微降低速度，直到当我停止它时它低于阈值。当我将它减少一个固定量(线性)时，它看起来不太正确，所以我需要模拟一个负加速度，但未能提出一个体面的简单公式如何计算我必须降低速度的量在每次迭代中。

更新:

感谢您到目前为止的回复，但我仍然无法从反馈中获得令人满意的功能。我可能没有很好地描述所需的解决方案，所以我将尝试举一个真实世界的例子来说明我想做什么样的计算:

假设某辆车在某条街道上行驶，司机将刹车踩到最大，直到汽车停下来。驾驶员在同一条街道上多次使用同一辆车执行此操作，但开始以不同的速度制动。当汽车减速时，我希望能够仅根据当前速度计算出一秒钟后的速度。对于这个计算，当司机开始刹车时汽车的行驶速度应该无关紧要，因为所有环境因素都保持不变。当然，公式中会有一些常数，但是当汽车下降到 30 m/s 时，它会在下一秒行驶相同的距离，无论驾驶员开始刹车时是以 100 还是 50 m/s 行驶.因此，自击中休息以来的时间也不是该函数的参数。一定速度下的减速度总是相同的。

在这种情况下，假设减速、质量、摩擦等任意常数并忽略空气阻力等复杂影响，您如何计算一秒后的速度？我只是在追求动能，并且由于打破汽车的摩擦而耗散它。

更新 2
我现在看到汽车的加速度将是线性的，这实际上不是我想要的。明天我会清理它并尝试新的建议。到目前为止，感谢您的投入。

Answer 1

[简短回答(假设 C 语法)]

double v(double old_v, double dt) {
    t = t_for(old_v); 
    new_t = t - dt; 
    return (new_t <= 0)?0:v_for(t);
} 

double t_for(double v)和 double v_for(double t)是从 v 到 t 双向映射(数学意义上的函数)的返回值，它是任意的，约束条件是它是单调的并且为 v >=0 定义(因此有一个点 v=0 )。一个例子是:

double v_for(double t) { return pow(t, k); }
double t_for(double v) { return pow(v, 1.0/k); }

哪里有:

k>1随着时间的推移，减速度以模数递减。

k<1随着时间的推移，减速度以模数增加。

k=1给出恒定的减速。

[更长的(有理由和情节)]

所以目标本质是:

查找函数 v(t+dt)=f(v(t),dt)获取当前速度值 v和时间增量 dt并返回当前速度 t+dt (它不需要实际指定 t，因为 v(t) 已经知道并作为参数提供，而 dt 只是时间增量)。换句话说，任务是实现一个例程double next_v(curr_v, dt);具有特定属性(见下文)。

[请注意] 有问题的函数有一个有用的(和期望的)属性，无论先前速度变化的“历史”如何，都返回相同的结果。这意味着，例如，如果连续速度系列是 [100, 50, 10, 0] (对于起始速度 v0=100 )，任何其他大于此的序列都将具有相同的“尾部”:[150 , 100, 50, 10, 0] (对于起始速度 v0=150 )等。换句话说，无论起始速度如何，所有速度-时间图都将有效地相互复制，只是沿时间偏移每个轴按其自己的值(参见下图，注意线 t=0.0 和 t=2.0 之间的绘图部分是相同的)。

此外，加速度w(t)=dv(t)/dt必须是时间的递减函数 t (为了我们在这里建模的移动 GUI 对象的视觉上令人愉悦和“直观”的行为)。

提议的想法是:

首先，您选择具有所需属性的单调速度函数(在您的情况下，它逐渐减小加速度，但是，如下例所示，使用“加速”函数更容易)。此函数不得也有上限，以便您可以将其用于任何大的速度值。此外，它必须有一个速度为零的点。一些例子是:v(t) = k*t (不完全是你的情况，因为减速 k 在这里是恒定的)，v=sqrt(-t) (这个没问题，在区间 t <= 0 上定义)。

然后，对于任何给定的速度，您可以在上述函数的绘图中找到具有该速度值的点(会有一个点，因为该函数不受约束，并且只有一个，因为它是单调的)，按时间增量向更小的速度前进值，从而获得下一个。迭代将逐渐(并且不可避免地)将您带到速度为零的点。

这基本上就是全部，甚至不需要产生一些“最终”公式，对时间值或初始(非当前)速度的依赖消失了，编程变得非常简单。

对于两个简单的情况，这个小的 python 脚本产生下面的图(给定的初始速度是 1.0 到 10.0 )，并且，正如你所看到的，从任何给定的速度“水平”和“向下”，图“表现”这当然是相同的，因为无论您以什么速度开始减速(减速)，您都将沿着相同的曲线相对于速度为零(变为)零的点“移动”:

import numpy
import pylab

import math


class VelocityCurve(object):
    """
    An interface for the velocity 'curve'.
    Must represent a _monotonically_ _growing_
        (i.e. with one-to-one correspondence
        between argument and value) function
        (think of a deceleration reverse-played)
    Must be defined for all larger-than-zero 'v' and 't'
    """
    def v(self, t):
        raise NotImplementedError

    def t(self, v):
        raise NotImplementedError



class VelocityValues(object):

    def __init__(self, v0, velocity_curve):
        assert v0 >= 0
        assert velocity_curve

        self._v = v0
        self._vc = velocity_curve

    def next_v(self, dt):
        t = self._vc.t(self._v)
        new_t = t - dt

        if new_t <= 0:
            self._v = 0
        else:
            self._v = self._vc.v(new_t)

        return self._v


class LinearVelocityCurve(VelocityCurve):

    def __init__(self, k):
        """k is for 'v(t)=k*t'"""
        super(LinearVelocityCurve, self).__init__()

        self._k = k

    def v(self, t):
        assert t >= 0
        return self._k*t

    def t(self, v):
        assert v >= 0
        return v/self._k


class RootVelocityCurve(VelocityCurve):

    def __init__(self, k):
        """k is for 'v(t)=t^(1/k)'"""
        super(RootVelocityCurve, self).__init__()

        self._k = k

    def v(self, t):
        assert t >= 0
        return math.pow(t, 1.0/self._k)

    def t(self, v):
        assert v >= 0
        return math.pow(v, self._k)


def plot_v_arr(v0, velocity_curve, dt):
    vel = VelocityValues(v0, velocity_curve)
    v_list = [v0]

    while True:
        v = vel.next_v(dt)
        v_list.append(v)

        if v <= 0:
            break

    v_arr = numpy.array(list(v_list))
    t_arr = numpy.array(xrange(len(v_list)))*dt

    pylab.plot(t_arr, v_arr)


dt = 0.1

for v0 in range(1, 11):
    plot_v_arr(v0, LinearVelocityCurve(1), dt)

for v0 in range(1, 11):
    plot_v_arr(v0, RootVelocityCurve(2), dt)


pylab.xlabel('Time ')
pylab.ylabel('Velocity')

pylab.grid(True)

pylab.show()

这给出了以下图(线性减速(即恒定减速)的线性图，“曲线”——对于“平方根”的情况(见上面的代码)):



另外请注意，要运行上述脚本，需要安装 pylab、numpy 和 friend (但仅对于绘图部分，“核心”类不依赖任何东西，当然可以单独使用)。

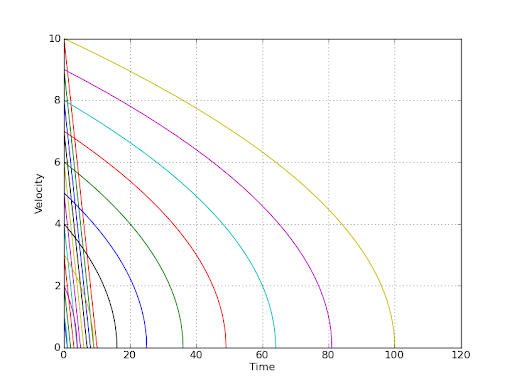
附言通过这种方法，人们可以真正“构建”(例如，为不同的 t 间隔增加不同的功能，甚至平滑手绘(记录)“人体工学”曲线)他喜欢的“拖动”:)