- html - 出于某种原因,IE8 对我的 Sass 文件中继承的 html5 CSS 不友好?
- JMeter 在响应断言中使用 span 标签的问题
- html - 在 :hover and :active? 上具有不同效果的 CSS 动画
- html - 相对于居中的 html 内容固定的 CSS 重复背景?
我仍然对所有这些类别理论的东西很熟悉,而且我看到的几乎每个例子都是关于 Maybe 或 Array 的。但我还没有找到任何区分这些类别的例子。例如,以下是一些我仍然无法回答的问题:
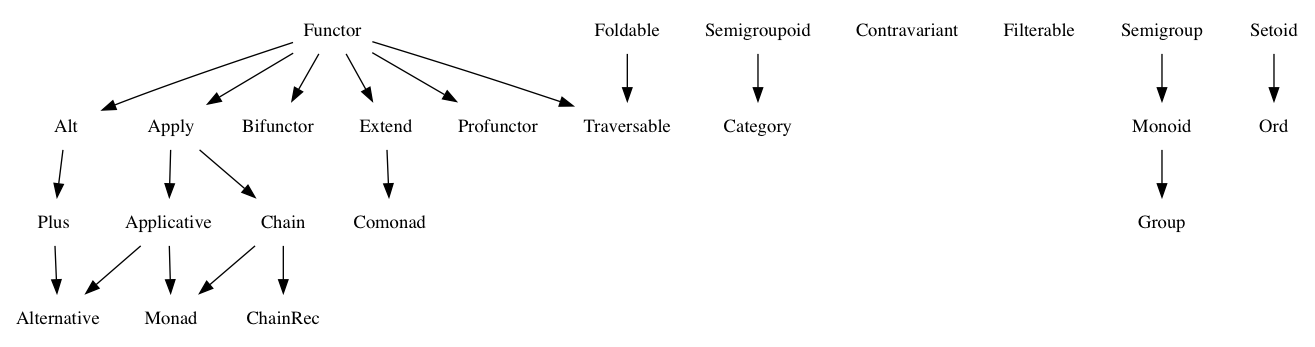
最佳答案
1. 什么是非 Monoid 的半群?
Cactus 给出了一个不是幺半群的半群的一个很好的例子。任何类型的非空(有限)列表表示该类型上的自由半群。另一个例子是 Data.Void.Void ,这不是 Monoid因为它没有任何元素,因此没有标识元素。另一个例子是加法下的正整数集合。
3. 什么是非 Apply 的 Functor?
一个Functor那不是 Apply是 Handler .
data Handler a where
Handler :: Exception e => (e -> IO a) -> Handler a
instance Functor Handler where
fmap f (Handler h) = Handler (\e -> f <$> h e)
Handler f :: Handler (a -> b)和
Handler g :: Handler a , 你有
f :: e1 -> IO (a -> b)
g :: e2 -> IO a
e1和
e2是(可能不同的)异常类型。您需要创建
h :: e3 -> IO b对于某些异常类型
e3 .没有真正明智的方法来做到这一点**。
Functor不能做成中规中矩的
Apply实例,因为
Apply只有一个定律,因此承认各种奇怪的事情,
Applicative会拒绝。
Map k和
IntMap .另外,
(,) a和
Const a当
a是
Semigroup但不是
Monoid .类似地,其他一些类型适合接受
Apply 的较弱上下文的模式。和/或
Bind比
Applicative或
Monad , 分别。
ZipList是
Apply但不是
Bind .我不知道
Chain 是什么是。
data P x y = P x y deriving (Show, Typeable)
instance (Exception x, Exception y) =>
Exception (P x y)
instance Apply Handler where
Handler f <.> Handler g =
Handler (\(P e1 e2) -> f e1 <*> g e2)
Apply法律,但我还不能完全确定。
关于haskell - 有哪些类型可以区分类别?,我们在Stack Overflow上找到一个类似的问题: https://stackoverflow.com/questions/36274369/
我正在尝试编写一个相当多态的库。我遇到了一种更容易表现出来却很难说出来的情况。它看起来有点像这样: {-# LANGUAGE ScopedTypeVariables #-} {-# LANGUAGE
谁能解释一下这个表达式是如何工作的? type = type || 'any'; 这是否意味着如果类型未定义则使用“任意”? 最佳答案 如果 type 为“falsy”(即 false,或 undef
我有一个界面,在IAnimal.fs中, namespace Kingdom type IAnimal = abstract member Eat : Food -> unit 以及另一个成功
这个问题在这里已经有了答案: 关闭 10 年前。 Possible Duplicate: What is the difference between (type)value and type(va
在 C# 中,default(Nullable) 之间有区别吗? (或 default(long?) )和 default(long) ? Long只是一个例子,它可以是任何其他struct类型。 最
假设我有一个案例类: case class Foo(num: Int, str: String, bool: Boolean) 现在我还有一个简单的包装器: sealed trait Wrapper[
这个问题在这里已经有了答案: Create C# delegate type with ref parameter at runtime (1 个回答) 关闭 2 年前。 为了即时创建委托(dele
我正在尝试获取图像的 dct。一开始我遇到了错误 The function/feature is not implemented (Odd-size DCT's are not implemented
我正在尝试使用 AFNetworking 的 AFPropertyListRequestOperation,但是当我尝试下载它时,出现错误 预期的内容类型{( “应用程序/x-plist” )}, 得
我在下面收到错误。我知道这段代码的意思,但我不知道界面应该是什么样子: Element implicitly has an 'any' type because index expression is
我尝试将 SignalType 从 ReactiveCocoa 扩展为自定义 ErrorType,代码如下所示 enum MyError: ErrorType { // .. cases }
我无法在任何其他问题中找到答案。假设我有一个抽象父类(super class) Abstract0,它有两个子类 Concrete1 和 Concrete1。我希望能够在 Abstract0 中定义类
我想知道为什么这个索引没有用在 RANGE 类型中,而是用在 INDEX 中: 索引: CREATE INDEX myindex ON orders(order_date); 查询: EXPLAIN
我正在使用 RxJava,现在我尝试通过提供 lambda 来订阅可观察对象: observableProvider.stringForKey(CURRENT_DELETED_ID) .sub
我已经尝试了几乎所有解决问题的方法,其中包括。为 提供类型使用app.use(express.static('public'))还有更多,但我似乎无法为此找到解决方案。 index.js : imp
以下哪个 CSS 选择器更快? input[type="submit"] { /* styles */ } 或 [type="submit"] { /* styles */ } 只是好
我不知道这个设置有什么问题,我在 IDEA 中获得了所有注释(@Controller、@Repository、@Service),它在行号左侧显示 bean,然后转到该 bean。 这是错误: 14-
我听从了建议 registering java function as a callback in C function并且可以使用“简单”类型(例如整数和字符串)进行回调,例如: jstring j
有一些 java 类,加载到 Oracle 数据库(版本 11g)和 pl/sql 函数包装器: create or replace function getDataFromJava( in_uLis
我已经从 David Walsh 的 css 动画回调中获取代码并将其修改为 TypeScript。但是,我收到一个错误,我不知道为什么: interface IBrowserPrefix { [

我是一名优秀的程序员,十分优秀!