Python 与 MATLAB 计算无穷大的积分，结果不同，替代方案(即将 Gauss-Legendre 正交扩展到 -x-> Infinity)？

Question

对于从 (-x 或 0) -> 无穷大的积分，我在 MATLAB 的 quadgk 和 Python 的 quad 例程之间得到不一致的结果。我相信 MATLAB 版本是正确的(基于将 flag 参数从 1 切换到 -1 的意义检查)，而 Python 版本给出错误的结果，在本例中为 0。MATLAB 产生 0.1022。 被积函数 是相同的，我已经列出了每一步，甚至将 MATLAB 的 quadgk 生成的 x 值插入到 Python 中(结果在 Python 版本中生成与 MATLAB 相同的值，只是将它们传递给 integrand 函数)。在这一点上，我希望使用另一个例程而不是 SciPy，例如这里的 Gauss-Legendre 正交 https://sourceforge.net/projects/fastgausslegendrequadrature/但我不确定如何将它从它的 a/b 范围扩展到 -a->infinity (我已经看到这些方法只能达到有限的数量:

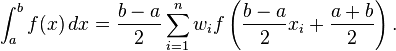Different intervals for Gauss-Legendre quadrature in numpy而 b=np.Inf 导致 NaN。也不确定如何从返回的节点和权重设置积分，虽然我一直在阅读转换但仅适用于 a 和 b 有限范围:https://pomax.github.io/bezierinfo/legendre-gauss.html或者如果有人知道可以处理这个的 Python 库 - 我真的不喜欢 quad 没有矢量化的事实并且可能会在 Cython 中编写代码，因为我必须集成 600,000快速运行(即链接到上面的 C++ 库链接)。这里真正奇怪的是，我设法通过将 vol 输入的任何位置上移 >= 0.39 来获得相同的结果，低于 Python 的结果在 0 处崩溃。非常令人困惑。感谢任何帮助，微积分已经有好几年了……这是 Python 代码:

from scipy.stats import norm, lognorm
from scipy.integrate import quad
import numpy as np

def integrand(x, flag, F, K, vol, T2, T1):
    d1 = (np.log(x / (x+K)) + 0.5 * (vol**2) * (T2-T1)) / (vol * np.sqrt(T2 - T1))
    d2 = d1 - vol*np.sqrt(T2 - T1)
    mu = np.log(F) - 0.5 *vol **2 * T1
    sigma = vol * np.sqrt(T1)
    value = lognorm.pdf(x, scale=np.exp(mu), s=sigma) * (flag * x*norm.cdf(flag * d1) - flag * (x+K)*norm.cdf(flag * d2))
    return value

if __name__ == '__main__':
        flag = 1
        F = 54.31
        K = 1.1967
        vol = 0.1328
        T2 = 0.0411
        T1 = 0.0137
        quad(integrand, 0, np.Inf, args=(flag, F, K, vol, T2, T1), epsabs=1e-12)[0]

这是 MATLAB 代码(必须将 被积函数 保存为 .M 然后可以在命令窗口中输入脚本):

function value = integrand(x, flag, F,K,vol,T2,T1)
d1 = (log(x ./ (x+K)) + 0.5 .* (vol.^2) .* (T2-T1)) ./ (vol .* sqrt(T2 - T1));
d2 = d1 - vol.*sqrt(T2 - T1);
mu = log(F) - 0.5 .*vol .^2 .* T1;
sigma = vol .* sqrt(T1);
value = lognpdf(x, mu, sigma) .* (flag .* x.*normcdf(flag .* d1) - flag .* (x+K).*normcdf(flag .* d2));
end

% 脚本部分

flag = 1
F = 54.31
K = 1.1967
vol = 0.1328
T2 = 0.0411
T1 = 0.0137
quadgk(@(x) integrand(x,flag, F, K, vol, T2, T1), 0, Inf, 'AbsTol',1e-12)

我应该注意到，当传递这些输入(转置以上变量)时，MATLAB 和 Python 使用 quad 生成相同的结果:

 current_opt = [  -1.0000    1.2075    0.1251    0.4300    0.0685    0.0411     
                1.0000    1.2075    0.0512    0.5600    0.0685    0.0411]  

Answer 1

好的，这很有趣。除非将 epsabs 变量设置得离谱地高，否则集成会分崩离析。我已经设法使用 epsabs=-1e1000 在 MATLAB 和 Python 之间复制结果。尽可能慢，但至少它有效。