algorithm - 点到面的最小距离

Question

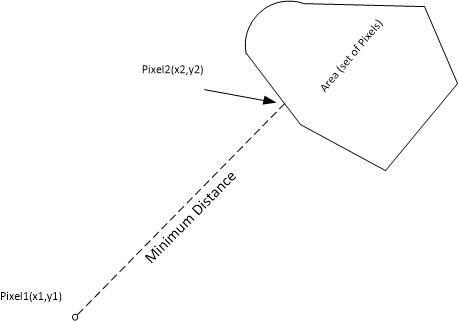
我试图在封闭区域中找到与点 (P1) 的距离最短的点 (P2)。该区域由同质像素构成，形状不完美，也不一定是凸的。这基本上是一个从最短路径到达一个区域的问题。

整个空间在内存中以位图的形式存储。找到 P2 的最佳方法是什么？我应该使用随机搜索(优化)方法吗？优化方法不会给出确切的最小值，但它们比强制使用该区域的每个像素要快。我需要在几秒钟内做出数千个这样的决定。

该区域的MinX,MinY,MaxX,MaxY可用。

谢谢。

Answer 1

这是我的代码，它是使用离散坐标的离散版本:

提示:我用来求Area周长的方法很简单，就像你从陆地上怎么知道海滩一样？答案:海滩从一侧被海覆盖，所以在我的图形矩阵中，NULL 引用是海，点是陆地!

课点:

class Point
{
    public int x;
    public int y;

    public Point (int X, int Y)
    {
        this.x = X;
        this.y = Y;
    }
}

课区:

class Area
{
    public ArrayList<Point> points;

    public Area ()
    {
        p = new ArrayList<Point>();
    }
}

离散距离实用类:

class DiscreteDistance
{

    public static int distance (Point a, Point b)
    {
        return Math.sqrt(Math.pow(b.x - a.x,2), Math.pow(b.y - a.y,2))
    }

    public static int distance (Point a, Area area)
    {
        ArrayList<Point> cir = circumference(area);
        int d = null;

        for (Point b : cir)
        {
            if (d == null || distance(a,b) < d)
            {
                d = distance(a,b);
            }
        }

        return d;
    }

    ArrayList<Point> circumference (Area area)
    {
        int minX = 0;
        int minY = 0;
        int maxX = 0;
        int maxY = 0;

        for (Point p : area.points)
        {
            if (p.x < minX) minX = p.x;
            if (p.x > maxX) maxX = p.x;
            if (p.y < minY) minY = p.y;
            if (p.y > maxY) maxY = p.y;
        }

        int w = maxX - minX +1;
        int h = maxY - minY +1;

        Point[][] graph = new Point[w][h];

        for (Point p : area.points)
        {
            graph[p.x - minX][p.y - minY] = p;
        }

        ArrayList<Point> cir = new ArrayList<Point>();

        for (int i=0; i<w; i++)
        {
            for (int j=0; j<h; j++)
            {
                if ((i > 0 && graph[i-1][j] == null)
                  || (i < (w-1) && graph[i+1][j] == null)
                  || (j > 0 && graph[i][j-1] == null)
                  || (i < (h-1) && graph[i][j+1] == null))
                {
                    cir.add(graph[i][j]);
                }
            }
        }

        return cir;
    }    
}