algorithm - 找到两个给定节点之间的路径？

Question

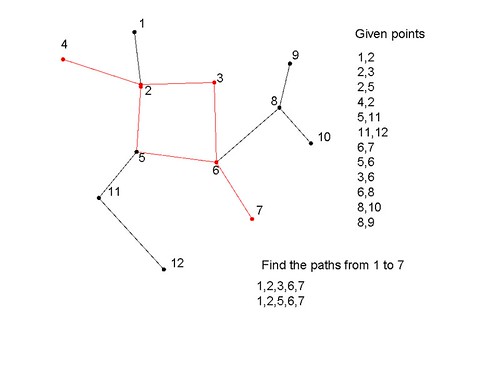
假设我有以下方式连接的节点，我如何得出给定点之间存在的路径数量以及路径详细信息？

1,2 //node 1 and 2 are connected
2,3
2,5
4,2
5,11
11,12
6,7
5,6
3,6
6,8
8,10
8,9

找到从1到7的路径:

回答:找到 2 条路径，它们是

1,2,3,6,7
1,2,5,6,7

实现发现 here很好，我将使用相同的

这是上面链接中的 python 代码片段

# a sample graph
graph = {'A': ['B', 'C','E'],
             'B': ['A','C', 'D'],
             'C': ['D'],
             'D': ['C'],
             'E': ['F','D'],
             'F': ['C']}

class MyQUEUE: # just an implementation of a queue

    def __init__(self):
        self.holder = []

    def enqueue(self,val):
        self.holder.append(val)

    def dequeue(self):
        val = None
        try:
            val = self.holder[0]
            if len(self.holder) == 1:
                self.holder = []
            else:
                self.holder = self.holder[1:]   
        except:
            pass

        return val  

    def IsEmpty(self):
        result = False
        if len(self.holder) == 0:
            result = True
        return result


path_queue = MyQUEUE() # now we make a queue


def BFS(graph,start,end,q):

    temp_path = [start]

    q.enqueue(temp_path)

    while q.IsEmpty() == False:
        tmp_path = q.dequeue()
        last_node = tmp_path[len(tmp_path)-1]
        print tmp_path
        if last_node == end:
            print "VALID_PATH : ",tmp_path
        for link_node in graph[last_node]:
            if link_node not in tmp_path:
                #new_path = []
                new_path = tmp_path + [link_node]
                q.enqueue(new_path)

BFS(graph,"A","D",path_queue)

-------------results-------------------
['A']
['A', 'B']
['A', 'C']
['A', 'E']
['A', 'B', 'C']
['A', 'B', 'D']
VALID_PATH :  ['A', 'B', 'D']
['A', 'C', 'D']
VALID_PATH :  ['A', 'C', 'D']
['A', 'E', 'F']
['A', 'E', 'D']
VALID_PATH :  ['A', 'E', 'D']
['A', 'B', 'C', 'D']
VALID_PATH :  ['A', 'B', 'C', 'D']
['A', 'E', 'F', 'C']
['A', 'E', 'F', 'C', 'D']
VALID_PATH :  ['A', 'E', 'F', 'C', 'D']

Answer 1

Breadth-first search遍历一个图，实际上找到了从起始节点开始的所有路径。但是，通常 BFS 不会保留所有路径。相反，它更新前驱函数 π 以保存最短路径。您可以轻松地修改算法，使 π(n) 不仅存储一个前驱，而且存储可能的前驱列表。

然后所有可能的路径都在此函数中编码，并通过递归遍历 π 得到所有可能的路径组合。

可以在 Cormen 等人 的算法导论 中找到使用此表示法的一个很好的伪代码，并随后在有关该主题的许多大学脚本中使用。谷歌搜索“BFS 伪代码前身 π”连根拔起this hit on Stack Exchange .