- Java锁的逻辑(结合对象头和ObjectMonitor)
- 还在用饼状图?来瞧瞧这些炫酷的百分比可视化新图形(附代码实现)⛵
- 自动注册实体类到EntityFrameworkCore上下文,并适配ABP及ABPVNext
- 基于Sklearn机器学习代码实战
贝塞尔曲线的切线及其AABB问题 。
2023 年抖音上居然还看到很多前端培训 。
各种直播前端教学(虽然是录播)但看起来还是有大批前往前端卷啊 。
说明了什么,很可能说明其它行业更难卷 。
这不是行业不景气业务下降了么.. 。
互联网行业是肉眼可见的不景气 。
业务量也下降了,业务相关的工作也变的不再饱和 。
我这 80 后的工作积极性降低了,啊..开始摆烂了 。
我还好赶上了前端发展的草莽时期,否则估计也进不了这个行档 。
怎么形容我自己呢,对编程是又菜又爱 。
可以将时间花一部分在自己感兴趣的内容上了,想到哪里干到哪里 。
而最近在翻译文章时贝塞尔曲线又回顾了一下 。
这让我想起了 2020 年遇到过的一个技术问题:曲线的 AABB 。
(另外还想到了两个其它问题也需要攻克一下, 怎么莫名的想到了鲁讯先生的朝花夕拾.. 果然是年纪大了..) 。
AABB 即图形界中常说的 AABB (axis-aligned bounding box) 包围盒, 严格来说是未能实现 BB 。
规则的图形很容易通过顶点距离就可以计算出 BB, 但像贝塞尔曲线这样的曲线就不太好算 。
是时候解决一下了 。
要实现的效果 。
在当年写了个简单绘图库 。
那是在 2020 年上一家公司,公司安排我负责微信小程序的开发 。
其中经常要用微信小程序生成海报,保存在图片用于在手机上的传播 。
单独手工去拼接生成海报还是比较麻烦的, Canvas 提供的 api 相对比较低级, 。
当时看到一些人开源出来的类似 json 配置形式生成海报图 。
这种配置类型的实现原理是大多是通过配置的坐标,大小,颜色,以及一些简单的 CSS 样式解析后在 canvas 上绘制 。
相对于纯手工去画,确实简单很多 。
但我更喜欢 Pixi.js、EaseJs 这类图形库的风格 。
当时就抽空写了一个简易的 Canvas 操作库 DuduCanvas 。
DuduCanvas 基本封装实现了图片,文本,形状等相关对象的绘制 。
调用的方式相比于配置要稍低级一点,拥有更大的自由度,例如添加一个圆形的头像图片:
const avatar = new Image({
image: loader.get('avatar'),
width: 100,
height: 100,
})
// 将头像变成圆形
avatar.borderRadius = '100%'
// 添加一个文本
const t1 = new Text()
t1.text = '你好世界Hello'
t1.color = 'red'
t1.x = 100
t1.y = 300
// 添加到舞台
stage.addChild(img, t1)
至少对于当时的项目来讲,DuduCanvas 运行的还不错,毕竟不是用它做动画或者游戏 。


还好,我代码存到了 github 上,在新公司临时做项目时还派上了用场用它画了个积分统计图 。

但它有几个缺点:
没有实现事件系统,当然它大部分时间只是用于生成海报,用不到事件交互 。
绘制曲线图形后的 BB 未能实现,需要自己手动指定 。
由于是 2020 年 当时微信小程序的 Canvas 2D 版本还牌测试版,所以使用的旧版 Canvas API 。
graphics 实现过于简单好多重复命令未去除 。
未能实现曲线的宽高计算(BB) 。
没过多久离职了,工作重心也从小程序转到其它前端项目 。
之后就没再管它 。
https://github.com/willian12345/DuduCanvas 。
2023 年我尝试着用微信开发者工具打开看了一下,还能运行 。
之前在翻译 贝塞尔曲线文字路径 一文中提到过三阶贝塞尔曲线 。
它是用 C# 伪代码来讲解的 。
定义 4 个控制点:
(x1, y1), (x2, y2), (x3, y3), (x4,y4)
定义 A..H 系数 。
A = x3 - 3 * x2 + 3 * x1 - x0
B = 3 * x2 - 6 * x1 + 3 * x0
C = 3 * x1 - 3 * x0
D = x0
E = y3 - 3 * y2 + 3 * y1 - y0
F = 3 * y2 - 6 * y1 + 3 * y0
G = 3 * y1 - 3 * y0
H = y0
得到多项式:
x = At3 + Bt2 + Ct + D
y = Et3 + Ft2 + Gt + H
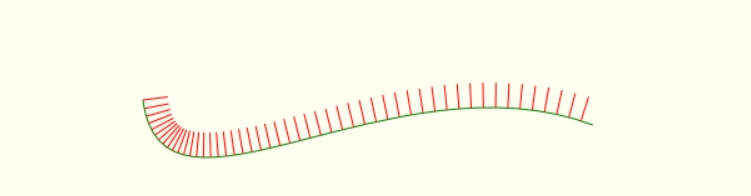
那么我们先用 Javascript 实现一下那篇文章中提到过的垂直于曲线的单位向量 。
假设我们要绘制的三阶贝塞尔曲线的四个控制点 。
[
{ x: 120, y: 320 },
{ x: 135, y: 440 },
{ x: 320, y: 280 },
{ x: 480, y: 340 },
];
下面是它三阶贝塞尔曲线采样点,t 取值 0-1 :
// 用 t 获取“样条曲线” 采样点
let sx = A * Math.pow(t, 3) + B * Math.pow(t, 2) + C * t + D
let sy = E * Math.pow(t, 3) + F * Math.pow(t, 2) + G * t + H
sx, sy 就是 t 从 0 - 1 时算出的曲线上的每个点 。
如果 t 取值足够小,那么在 canvas 上画出所有的点它就是一条贝塞尔曲线 。
t 间隔为 0.1 时

t 间隔为 0.001 时
画出垂直于曲线的向量关键, 在于对三阶贝塞尔曲线多项式的求导 。
如果你忘记了什么是求导(导函数), 没关系, 直接用公式就完了 。
我这个学渣都会用,你肯定也可以, 。
当然最好是回去复习一下高中后期的导函数部分,有助于理解曲线切线的几何意义 。
求导后得到向量:
// 求导前
x = At3 + Bt2 + Ct + D
y = Et3 + Ft2 + Gt + H
// 求导后
Vx = 3At2 + 2Bt + C
Vy = 3Et2 + 2Ft + G
用 Javascript 实现如下:
// (求导)用于计算曲线上采样点的切线向量
let tx = 3 * A * Math.pow(t, 2) + 2 * B * t + C
let ty = 3 * E * Math.pow(t, 2) + 2 * F * t + G
// 旋转 90 度或 270 度垂直于曲线采样点
let px = ty
let py = -tx
// 缩至单位向量
let magnitude = Math.sqrt(px * px + py * py)
px = px / magnitude
py = py / magnitude
// 为了向量可见,扩大 20 个单位
px *= 20;
py *= 20;
// 从采样点连接至切线向量偏移位置
console.log(sx + px, sy + py);
源码尽量平铺直叙:... 。
https://github.com/willian12345/blogpost/blob/main/curve/bezier/cubic-bezier-tangent-test.html 。
如果你对贝塞尔曲线感兴趣还可以看一下我翻译的《曲线编程艺术》的 贝塞尔曲线 这一章 。
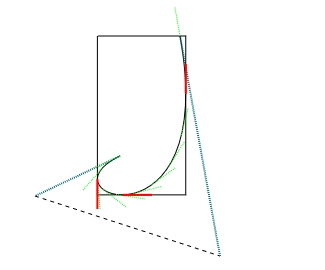
要实现三阶贝塞尔曲线的AABB(包围合)还是得从切线入手 。
比如像下面这个曲线 。
let points = [
{x: 120, y: 160 },
{x: 35, y: 200 },
{x: 220, y: 260 },
{x: 180, y: 40 },
];
四个点得出的结果:

先把它的四个点用直线连接画出来 。
ctx.beginPath();
ctx.lineWidth = 2;
ctx.setLineDash([1, 2]);
ctx.strokeStyle = '#076c75';
ctx.moveTo(points[0].x, points[0].y);
ctx.lineTo(points[1].x, points[1].y);
ctx.stroke()
ctx.beginPath();
ctx.lineWidth = 1;
ctx.moveTo(points[1].x, points[1].y);
ctx.strokeStyle = 'black';
ctx.lineTo(points[2].x, points[2].y);
ctx.stroke()
ctx.beginPath();
ctx.lineWidth = 2;
ctx.strokeStyle = '#076c75';
ctx.moveTo(points[2].x, points[2].y);
ctx.lineTo(points[3].x, points[3].y);
ctx.stroke();
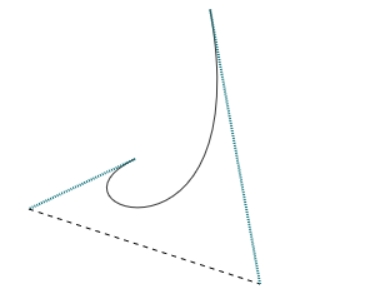
蓝色的线就像是控制手柄 。
点 points[1] 和 points[2] 分别就是控制手柄 。
控制手柄就是 PS 内的钢笔工具用过吧?就是这个,长短与位置调节就控制了曲线的形状 。
BB 包围盒就是找到曲线所有转折点中最小和最大的转折点 。
找转折点,可理解为找到曲线上的斜率 。
还是从公式入手 。
在上一节中贝塞尔公式系数直接把 x, y 都用 A..H 表示出来了 。
这次先简化到一维比如 x , 系数用 A..D 表示 。
x 坐标方程即(y 轴坐标方程其实是一样的,只是算了两遍):
x = A (1-t)^3 +3 B t (1-t)^2 + 3 C t^2 (1-t) + D t^3
对其求导,关于 t 的微分,得到微分方程 。
dx/dt = 3 (B - A) (1-t)^2 + 6 (C - B) (1-t) t + 3 (D - C) t^2
= [3 (D - C) - 6 (C - B) + 3 (B - A)] t^2
+ [ -6 (B - A) - 6 (C - B)] t
+ 3 (B - A)
= (3 D - 9 C + 9 B - 3 A) t^2 + (6 A - 12 B + 6 C) t + 3 (B - A)
合并整理后是一个二次函数:
dx/dt = (3 D - 9 C + 9 B - 3 A) t^2 + (6 A - 12 B + 6 C) t + 3 (B - A)
用其 a, b, c 简化系数代替后:
dx/dt = a t^2 + b t + c
我们要解决的是 dx/dt = 0 。
"斜率为 0 可能意味着曲线在该点处有一个极小值或极大值,或者曲线在该点处是一个水平切线" 。
反正我这个学渣是这么理解的 。
那么就是对二交方程求解 。
a t^2 + b t + c = 0 。
可用求根公式 。
- b +/- sqrt(b^2-4 a c)
-----------------------
2 a
解方程可得 两个解(根) t0, t1, 无解,或 1 个解 。
这就有了四个点的极值,起点,终点,和两个解 。
系数 a, b, c 就是根据公式代入, 比如 x 的坐标代入后:
let a = 3 * points[3].x - 9 * points[2].x + 9 * points[1].x - 3 * points[0].x;
let b = 6 * points[0].x - 12 * points[1].x + 6 * points[2].x;
let c = 3 * points[1].x - 3 * points[0].x;
还记得初中数学如何判断二次函数有几个根吧?
delta 即 b^2-4ac 判断 大于等于 0 即为有解 。
let delta = b * b - 4 * a * c;
判断有解后找到局部极限值 (local extreme) 。
代入求根公式
t1 = (-b + Math.sqrt(delta)) / (2 * a);
t2 = (-b - Math.sqrt(delta)) / (2 * a);
我们只关心 0 <= t <= 1 的情况 。
将得到和 t1, t2 分别代入贝塞尔曲线公式 。
x = A (1-t)^3 +3 B t (1-t)^2 + 3 C t^2 (1-t) + D t^3
得到的就是真实的 x 坐标值, 。
所以需 x 要判断 。
if (x < xl) xl = x;
if (x > xh) xh = x;
记住是求出的二个根 t1, t2 分别代入判断 。
它有可能是最大值,也有可能是最小值 记作: xl, xh 。
对 y 同样进行一模一样的计算,t3, t4 也可以得到一最大值与最小值 记作:yl, yh 。
将它们从起点 左下,左上,右上,右下,左下终点 的顺序连接起来就是我们要的 BB 包围盒 。
ctx.moveTo(xl, yl); // 起点,左下
ctx.lineTo(xl, yh); // 左上
ctx.lineTo(xh, yh); // 右上
ctx.lineTo(xh, yl); // 右下
ctx.lineTo(xl, yl); // 终点,左下
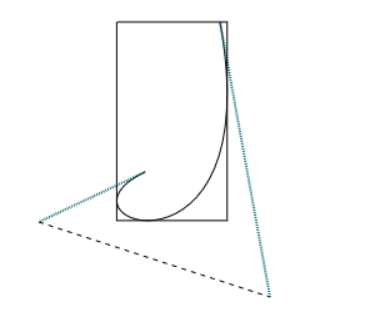
如上图,包围盒围起来了,解决了计算贝塞尔曲线宽高计算的问题 。
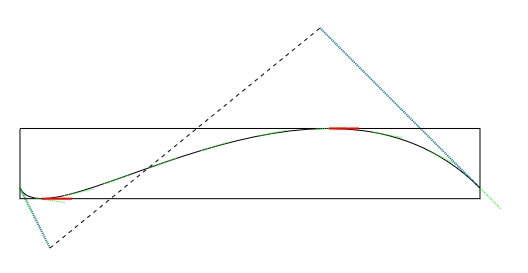
再把曲线的切线画出来,这回我们不画垂直向量,直接画切线 。
切线向量这道菜已经吃过了.. 。
将 t 步长设为 0.1, 进行曲线采样, 画出绿色的切线 。
for( let t=0; t <=1; t += 0.1){
// 绘制起点移动到对应的曲线点上
const sx = calcBezierByT(pointXArray, t);
const sy = calcBezierByT(pointYArray, t);
ctx.moveTo(sx, sy)
// a t^2 + b t + c
// 切线向量
let vx = a1 * Math.pow(t,2) + b1 * t + c1
let vy = a2 * Math.pow(t,2) + b2 * t + c2
// 缩至单位向量
let magnitude = Math.sqrt(vx * vx + vy * vy)
// vx = -vx / magnitude;
// vy = -vy / magnitude;
vx = vx / magnitude;
vy = vy / magnitude;
// 向量长度变长 30 个单位
vx *= 30
vy *= 30
ctx.strokeStyle = 'green';
ctx.lineTo(sx + vx, sy + vy);
}
ctx.stroke();
}
(绿色颜色有点儿淡了感觉...) 。
代入上一节算出的 t1, t2, t3, t4 用红色画出局部极限值 (local extreme) 验证 。
注意 曲线不同,t1, t2, t3, t4 的值有可能有,有可能没有,且我们需要的是 t1 >= 0 。
需要这样处理 。
// 过滤
const tArray = [t1, t2, t3, t4].filter((t)=> t >= 0);
for( let i=0; i <= tArray.length; i++){
...与上面生成切线一样,只是 t 值是从 tArray 获取,而不是 0.1 步长
}
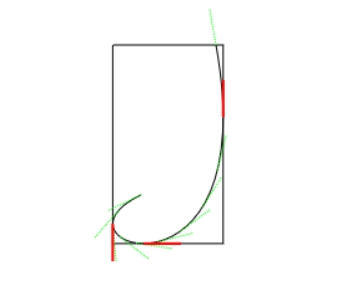
可以看到,红色标出的果然很 “极限” 。
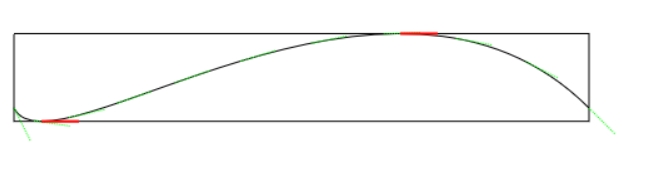
代入不同的坐标值看看 。
const points = [
{ x: 20, y: 340 },
{ x: 50, y: 400 },
{ x: 320, y: 180 },
{ x: 480, y: 340 },
];
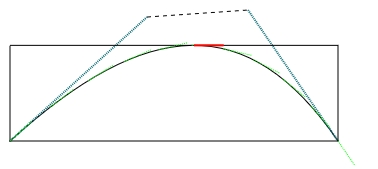
const points = [
{x: 13, y: 224 },
{x: 150, y: 100 },
{x: 251, y: 93 },
{x: 341, y: 224 },
];
(绿色颜色快看不出来了,PC上的微信截图工具会模糊截图...) 。
可以看到,有些曲线极限值就不一定有四个 。
https://github.com/willian12345/blogpost/blob/main/curve/bezier/aabb.html 。
贝塞尔曲线虽然原理很简单,但深入后就会特别复杂,你们好好深入,反正以我的能力是深入不了的 。
作为一个打工人,就要有打工人的觉悟,主打一个随意,没必要在一个问题上死磕 。
东看看,西看看,说不定回头再来看问题,已具备足够的知识与资料后就解决了 。
创业公司麻,就是这么的不稳定,何况是在这样一个环境下 。
最近公司要让我重新再接触 unity ,这又绕回来了, c# 其实挺好的 。
参考资料
https://developer.mozilla.org/zh-CN/docs/Web/API/CanvasRenderingContext2D/bezierCurveTo 。
https://floris.briolas.nl/floris/2009/10/bounding-box-of-cubic-bezier/ 。
https://stackoverflow.com/questions/24809978/calculating-the-bounding-box-of-cubic-bezier-curve 。
https://pomax.github.io/bezierinfo/#boundingbox 。
博客园: http://cnblogs.com/willian/ github: https://github.com/willian12345/ 。
最后此篇关于贝塞尔曲线的切线及其AABB问题的文章就讲到这里了,如果你想了解更多关于贝塞尔曲线的切线及其AABB问题的内容请搜索CFSDN的文章或继续浏览相关文章,希望大家以后支持我的博客! 。

我是一名优秀的程序员,十分优秀!