二分法是搜索算法中极其典型的方法，其要求输入序列有序并可随机访问。算法思想为 。

输入：有序数组nums，目的数值target 要求输出：如果target存在在数组中，则输出其index，否则输出-1 。

1. 将原数组通过[left,right]两个索引划分范围，初值left=0,right=数组的最后一个元素
2. 当left <= right时
   1. middle = (left + right)/2
   2. 判断nums[middle]是不是要查找的target，如果是则返回结果
   3. 判断nums[middle]> target，证明要查找的target在左边，因此right = middle - 1
   4. 判断nums[middle]< target，证明要查找的target在右边，因此left = middle + 1
3. 没有查找到return -1。

形如下图:

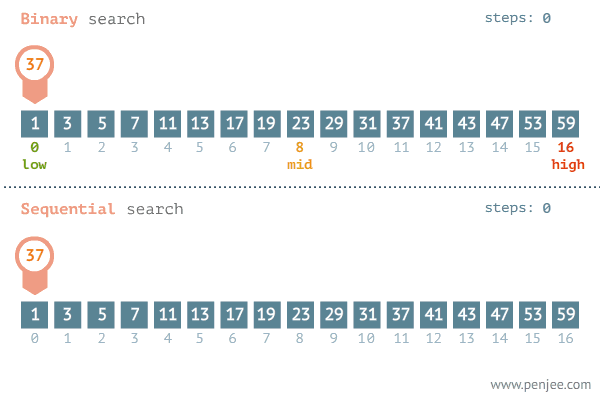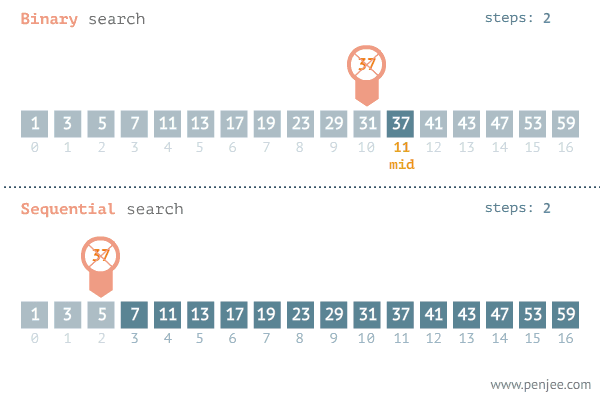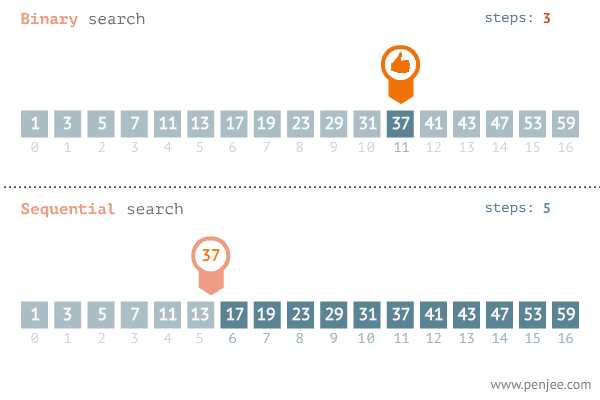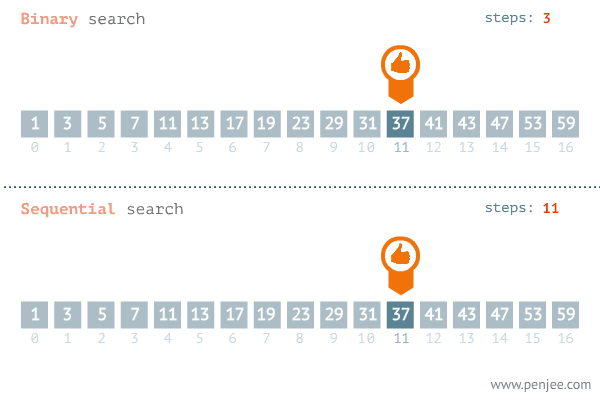
传统的二分法代码如下:

                        
                          func binarySearch(nums []int, target int) int {
	left, right := 0, len(nums)-1
	for left <= right {
		middle := (left + right) / 2
		if nums[middle] == target {
			return middle
		} else if nums[middle] > target {
			right = middle - 1
		} else {
			left = middle + 1
		}
	}
	return -1
}

                        
                      

这里要注意两个问题:

1. 上述算法中的第2步中 = 的判断，即 for left <= right 还是 for left < right 。
2. 上述算法2.2-2.4中的判断条件以及下一次查找区间的设置
3. 返回值代表什么意思

for left<= right 中 = 的判断

首先对于第一个问题， = 是否应该存在，取决于对于二分查找的初始化定义，例如:

1. 如果二分查找遍历的区间采用 [left,right]（数学中的双闭区间） 的形式，考虑 left==right 即 = 成立的情况，则表示 区间内只有单个操作数 ，这种情况还是需要处理，否则无法通过其余方式表示这种情况，所以此时 = 是必须的。
2. 如果二分查找遍历的区间采用 [left,right) 的形式，考虑 left==right 即 = 成立的情况，事实证明，这种情况并不应该存在，我们无法用 [i,i) 表示任何一个区间，所以，这种情况下， = 就不是必须的。

判断条件以及下一次查找区间的设置

然后考察对于第二个问题， 判断条件以及下一次查找区间应该如何设置 ?

注意 ：二分查找是一个经典的 查找算法 ，其目的是 查找到指定的位置或者值 ，并不仅限于 查找到等于target的index 这一种情况.

但无论怎样，二分查找本身有一个固定模式，即 二分 ，就是从middle处将区间[left,right]分成两份，然后根据middle的情况查找（或者更新新的区间），因此，我们只需要考虑清楚如下三种条件时要怎么处理即可:

1. 当遍历到nums[middle] == target时应该怎样处理（新的查找区间是什么），即当前值等于目标值
2. 当遍历到nums[middle] > target时应该怎样处理（新的查找区间是什么），即当前值大于目标值
3. 当遍历到nums[middle] < target时应该怎样处理（新的查找区间是什么），即当前值小于目标值

讨论完上述两个问题，其实二分法就有了一个固定的框架:

                        
                          func binarySearch(nums []int, target int) int {
	left, right := 0, len(nums)-1
	for left <= right {
		middle := (left + right) / 2
		if nums[middle] == target {
			// 当前值等于目标值时，如何处理（新的查找区间是什么）
		} else if nums[middle] > target {
			// 当前值大于目标值时，如何处理（新的查找区间是什么）
		} else {
			// 当前值小于目标值时，如何处理（新的查找区间是什么）
		}
	}
    // 考虑返回值的意义
	return 
}

                        
                      

返回值的含义

最后我们讨论 返回值的含义 这一话题。在传统的 二分查找 中，只有在两种情况下会返回:

1. 查找到目标target，返回查找到的index
2. 未查找到目标target，返回-1。（即文章最起始处 步骤3的含义）

这里返回值的含义表示 target在nums中的index ，该值只会出现在 nums[middle]==target 这一条件下。然而，刚才提到了 二分查找不总是处理等式条件 ，因此我们总要思考两种返回值的含义:

1. nums[middle]==target，这时return代表的是什么？
2. 数组中不存在target，此时return的是什么，此时left、right代表什么？

这里我们举一个稍稍复杂一点的例子对二分查找进行分析.

• 搜索插入位置
• 在排序数组中查找元素的第一个和最后一个位置

搜索插入位置

题目要求如下:

这个问题要求返回两种返回值:

1. 在数组中找到目标值，并返回其索引
2. 如果目标值不存在于数组中，返回它将会被按顺序插入的位置

其中对于情况1，传统的二分查找算法就可以解决，而情况2，则需要借助于本部分要讲解的 返回值的含义 .

对于传统的二分法:

                        
                          func binarySearch(nums []int, target int) int {
	left, right := 0, len(nums)-1
	for left <= right {
		middle := (left + right) / 2
		if nums[middle] == target {
			return middle
		} else if nums[middle] > target {
			right = middle - 1
		} else {
			left = middle + 1
		}
	}
	return -1
}

                        
                      

如果target能在nums数组中查找到，必定最终查找到一个[i,i]类型的区间，即区间中只有一个数字，否则区间就要再次进行二分。例如：如果要在下列数组中查找4所在的位置，查找过程如下，第三步时，查找区间为[2,3]，有两个值，无法确定答案，则需要再次进行一次查找:

                        
                          target == 4
nums   1  2  3  4
index  0  1  2  3
1      l        r
2         l     r
3            l  r
4               lr 

                        
                      

那么最终我们处理的情况必定是对于区间[left,right]中，其中left == right，因此middle == left == right，此时nums[middle]和target的关系.

• nums[middle] > target，则需要从middle左侧继续寻找，right = middle - 1，注意此时left = middle，left > right
• nums[middle] < target，则需要从middle右侧继续寻找，left = middle + 1，注意此时right = middle，left > right

所以此时，left指向的永远是大的那个值，right是小的那个值（ 因为left <= right时，循环不会终止，循环终止条件为left > right，根据数组的有序性，nums[left] > nums[right] ）.

最后，我们考察该题，对于数组nums，如果目标值不在其中，那么其最终查找到的值只有两种情况:

1. nums[middle] < target，此时nums[middle]应该是第一个小于target的值，如果要查找target所在位置，应该返回 大于middle的index ，即 left
2. nums[middle] > target，此时nums[middle]应该是第一个大于target的值，如果要查找target所在位置，应该返回 等于middle的index ，用target替换middle位置的值，即 left

因此，该题的结果，只需要修改传统二分查找的最后一行:

                        
                          func binarySearch(nums []int, target int) int {
	left, right := 0, len(nums)-1
	for left <= right {
		middle := (left + right) / 2
		if nums[middle] == target {
			return middle
		} else if nums[middle] > target {
			right = middle - 1
		} else {
			left = middle + 1
		}
	}
	return left 
}

                        
                      

在排序数组中查找元素的第一个和最后一个位置

题目要求如下:

注意这里查找的是 元素第一次和最后一次出现的位置 ，这里我们以 查找第一次出现的位置举例 ，后者同理.

考察我们在 判断条件以及下一次查找区间的设置 中强调的，考察二分查找的三种情况:

情况	分析	操作
nums[middle] == target时，即当前值等于目标值	第一次出现的位置 可能 在当前值 前面	right = middle - 1
nums[middle] > target时，即当前值大于目标值	第一次出现的位置在当前值 前面	right = middle - 1
nums[middle] < target时，即当前值小于目标值	第一次出现的位置在当前值 后面	left = middle + 1

与之前不同的是当 nums[middle] == target 时，不再有返回值了，那么考虑最后返回值的含义，最终 left > right 时情况有如下3种:

情况	分析	操作
nums[middle] == target	此时，middle前的值必定<middle，而不是等于（只要等于，考虑上表的情况1，会使right = middle - 1）	return left
nums[middle] > target	此情况不存在，因为如果有这种情况会继续使right=middle-1	不进行操作
nums[middle] < target	此时middle必定是target前的第一个元素	return left

经过上面的分析后，可以清晰的写出代码:

                        
                              l, r := 0, len(nums)-1
	for l <= r {
		m := (l + r) / 2
		if nums[m] >= target {
			r = m - 1
		} else {
			l = m + 1
		}
	}
    result := l

                        
                      

而查找元素出现的最后一个位置，只需要反过来，最后return right即可。代码如下:

                        
                              l, r: = 0, len(nums)-1
	for l <= r {
		m := (l + r) / 2
		if nums[m] <= target {
			l = m + 1
		} else {
			r = m - 1
		}
	}
    result := r

                        
                      

总结

本文详细分析了二分查找的所有细节，对于二分查找处理的问题，我们常常需要更加关注本文讨论的后两个问题:

1. 判断条件以及下一次查找区间的设置
2. 返回值的含义

最后填充模版即可.

                        
                          func binarySearch(nums []int, target int) int {
	left, right := 0, len(nums)-1
	for left <= right {
		middle := (left + right) / 2
		if nums[middle] == target {
			// 当前值等于目标值时，如何处理（新的查找区间是什么）
		} else if nums[middle] > target {
			// 当前值大于目标值时，如何处理（新的查找区间是什么）
		} else {
			// 当前值小于目标值时，如何处理（新的查找区间是什么）
		}
	}
    // 考虑返回值的意义
	return 
}

                        
                      

最后此篇关于Leetcode刷题笔记——二分法的文章就讲到这里了,如果你想了解更多关于Leetcode刷题笔记——二分法的内容请搜索CFSDN的文章或继续浏览相关文章，希望大家以后支持我的博客！ 。