- Java锁的逻辑(结合对象头和ObjectMonitor)
- 还在用饼状图?来瞧瞧这些炫酷的百分比可视化新图形(附代码实现)⛵
- 自动注册实体类到EntityFrameworkCore上下文,并适配ABP及ABPVNext
- 基于Sklearn机器学习代码实战
Note:[ wechat:Y466551 | 可加勿骚扰,付费咨询 ] 。
论文标题:MetaAdapt: Domain Adaptive Few-Shot Misinformation Detection via Meta Learning 论文作者:Zhenrui Yue、Huimin Zeng、Yang Zhang、Lanyu Shang、Dong Wang 论文来源:2023 ACL 论文地址:download 论文代码:download 视屏讲解:click 。
出发点:域偏移导致的性能下降 ; 。
简介:为了解决数据稀缺性的问题,提出了一种基于元学习的领域自适应小样本错误信息检测方法。MetaAdapt 利用有限的目标例子来提供反馈,并指导从源领域到目标领域的知识转移。特别地,本文用多个源任务来训练初始模型,并计算它们与元任务的相似性得分。基于相似性得分,重新调整了元梯度,以自适应地从源任务中学习; 。
。
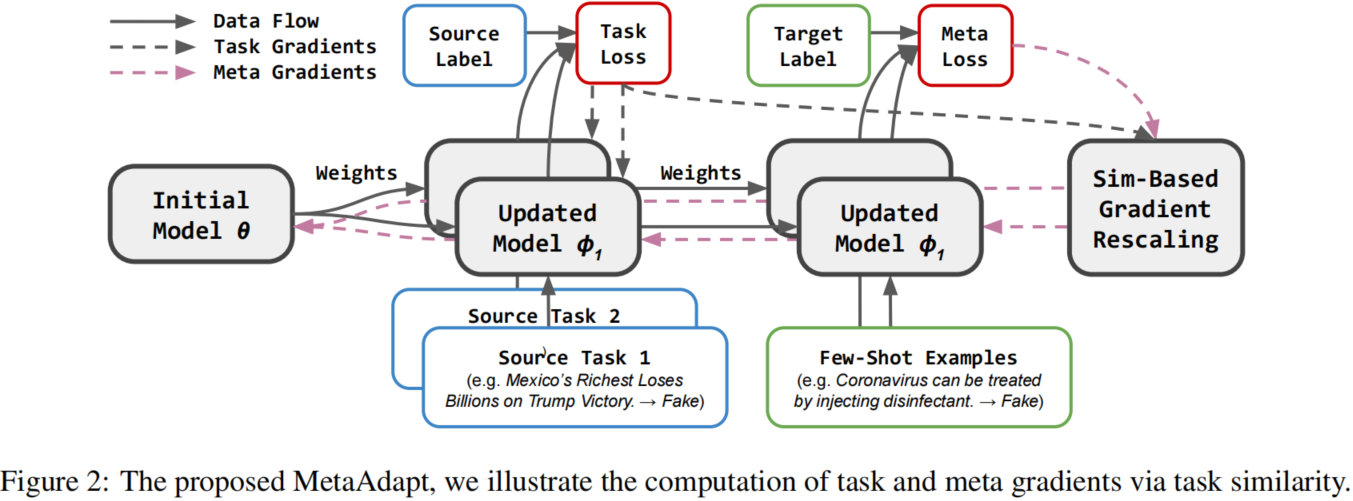
场景 :
小样本元域适应:源域带标记数据+目标域 k-shot 带标记数据; 。
双层优化目标(训练目标):
$\underset{\boldsymbol{\theta}}{\text{min}}\frac{1}{n} \sum^{n} \mathcal{L}\left(\mathcal{A} l g\left(\boldsymbol{\theta}, \operatorname{Sampler}\left(\boldsymbol{X}_{s}\right)\right), \boldsymbol{X}_{t}^{\prime}\right) \quad\quad(1)$ 。
内部优化目标(源域):
$\mathcal{A} l g(\boldsymbol{\theta}, \boldsymbol{X})=\boldsymbol{\phi}=\boldsymbol{\theta}-\alpha \nabla_{\boldsymbol{\theta}} \mathcal{L}(\boldsymbol{\theta}, \boldsymbol{X}) \quad\quad(2)$ 。
任务梯度(task gradient):
$\text{task gradient}\doteq \phi_{i}-\theta \quad\quad(3)$ 。
其中:
$\begin{array}{l}\phi &= \frac{d \mathcal{L}\left(\mathcal{A l g}(\boldsymbol{\theta}, \boldsymbol{X}), \boldsymbol{X}_{t}^{\prime}\right)}{d \boldsymbol{\theta}}\\&=\quad \frac{d \mathcal{A l g}(\boldsymbol{\theta}, \boldsymbol{X})}{d \boldsymbol{\theta}} \nabla_{\boldsymbol{\phi}} \mathcal{L}\left(\mathcal{A l g}(\boldsymbol{\theta}, \boldsymbol{X}), \boldsymbol{X}_{t}^{\prime}\right)\end{array}\quad\quad(4)$ 。
元梯度(meta gradient):
假设 :如果任务梯度和元梯度产生较高的相似性得分,则参数在内环和外环优化中都收敛到相同的方向; 。
假设源域上存在 $n$ 个任务,则得到 $n$ 个相似性得分:
$s_{i}=\operatorname{CosSim}\left(\phi_{i}-\boldsymbol{\theta}, \frac{d \boldsymbol{\phi}_{i}}{d \boldsymbol{\theta}} \nabla_{\boldsymbol{\phi}_{i}} \mathcal{L}\left(\boldsymbol{\phi}_{i}, \boldsymbol{X}_{t}^{\prime}\right)\right)\quad\quad(5)$ 。
因此,计算相似性得分概率分布:
$s=\operatorname{softmax}\left(\left[\frac{s_{1}}{\tau}, \frac{s_{2}}{\tau}, \ldots, \frac{s_{n}}{\tau}\right]\right) \quad\quad(6)$ 。
目标域参数的更新如下(任务相似性得分加权):
$\boldsymbol{\theta}-\beta \sum_{i}^{n} s_{i} \cdot \frac{d \boldsymbol{\phi}_{i}}{d \boldsymbol{\theta}} \nabla_{\boldsymbol{\phi}_{i}} \mathcal{L}\left(\boldsymbol{\phi}_{i}, \boldsymbol{X}_{t}^{\prime}\right) \quad\quad(7)$ 。

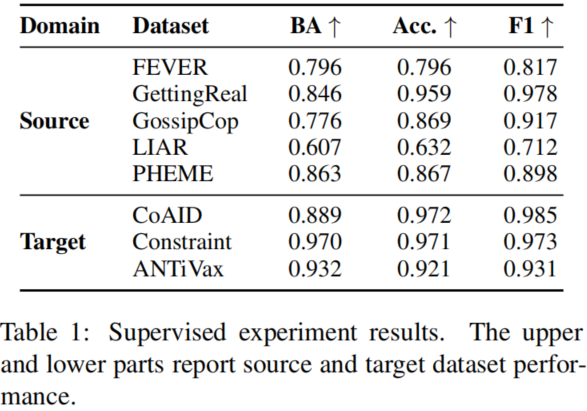
监督训练 。
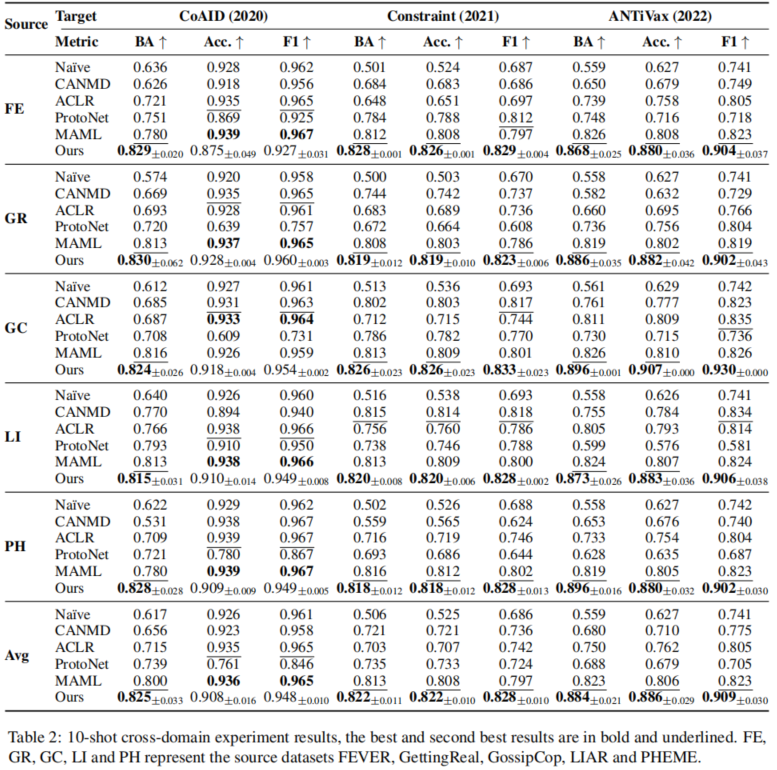
小样本元域适应 。
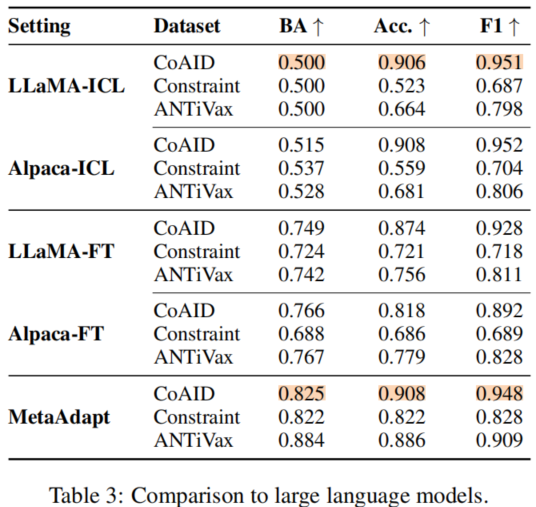
大模型 。
鲁棒性研究 。

消融研究 。

最后此篇关于论文解读(MetaAdapt)《MetaAdapt:DomainAdaptiveFew-ShotMisinformationDetectionviaMetaLearning》的文章就讲到这里了,如果你想了解更多关于论文解读(MetaAdapt)《MetaAdapt:DomainAdaptiveFew-ShotMisinformationDetectionviaMetaLearning》的内容请搜索CFSDN的文章或继续浏览相关文章,希望大家以后支持我的博客! 。
我在这里的意图是创建一个单线程的 will-make-you-a-better-programmer-just-for-reading 之类的 文章 或 论文 或 真正站起来的博文作者付出了很多努力来
我想知道是否有人有很好的资源可以阅读或编写代码来试验“自动完成” 我想知道自动完成背后的理论是什么,从哪里开始什么是常见的错误等。 我发现 Enso、Launchy、Google chrome 甚至
市场上有许多工具,如 MPS,它们促进了面向语言的编程,据说这使程序员能够为任务设计(理想的?)语言。出于某种原因,这听起来既有趣又无聊,所以我想知道是否有人知道并可以推荐有关该主题的文章。 谢谢 最
我正在编写一个使用 JointJS 来显示图表的应用。 但是,我希望能够在页面中动态添加和删除图表。添加新图表相当简单,但是当我删除图表时,删除 DOM 元素并让图表和纸张对象被垃圾收集是否安全? 最
我在声明非成员函数listOverview()时出错; void listOverview() { std::cout #include class Book; class Paper
关闭。这个问题需要更多focused .它目前不接受答案。 想改进这个问题吗? 更新问题,使其只关注一个问题 editing this post . 关闭 3 年前。 Improve this qu
我正在将 Raphael 与 Meteor 一起使用,但遇到了问题。我正在创建一个 paper通过使用 var paper = Raphael("paper", 800, 600);如果我将此代码放在
我正在使用acm LaTeX template我在使纸张双倍行距时遇到困难。 我的 LaTeX 文档如下所示: \documentclass{acm_proc_article-sp} \usepack
H.Chi Wong、Marshall Bern 和 David Goldberg 的论文“An Image Signature for any kind image”中提到的算法步骤背后的原因是什么
我一直在使用Microsoft Academic Knoledge API一周了,直到现在我还没有遇到任何问题。我想获取某个 session 的所有论文,例如 ICLR 或 ICML。我正在尝试使用从
我正在读这篇论文Understanding Deep learning requires rethinking generalization我不明白为什么在第 5 页第 2.2 节“含义、Redema
就目前情况而言,这个问题不太适合我们的问答形式。我们希望答案得到事实、引用资料或专业知识的支持,但这个问题可能会引发辩论、争论、民意调查或扩展讨论。如果您觉得这个问题可以改进并可能重新开放,visit
我必须为非程序员(我们公司的客户)创建一个 DSL,它需要提供一些更高级别的语言功能(循环、条件表达式、变量...... - 所以它不仅仅是一个“简单”的 DSL)。 使用 DSL 应该很容易;人们应
在卷积神经网络中梯度数据的可视化中,使用 Caffe 框架,已经可视化了所有类的梯度数据,对特定类采用梯度很有趣。在“bvlc_reference_caffenet”模型的 deploy.protot
auto(x)表达式被添加到语言中。一个理性的原因是我们无法以此完善前向衰减。 template constexpr decay_t decay_copy(T&& v) noexcept( i

我是一名优秀的程序员,十分优秀!