- Java锁的逻辑(结合对象头和ObjectMonitor)
- 还在用饼状图?来瞧瞧这些炫酷的百分比可视化新图形(附代码实现)⛵
- 自动注册实体类到EntityFrameworkCore上下文,并适配ABP及ABPVNext
- 基于Sklearn机器学习代码实战
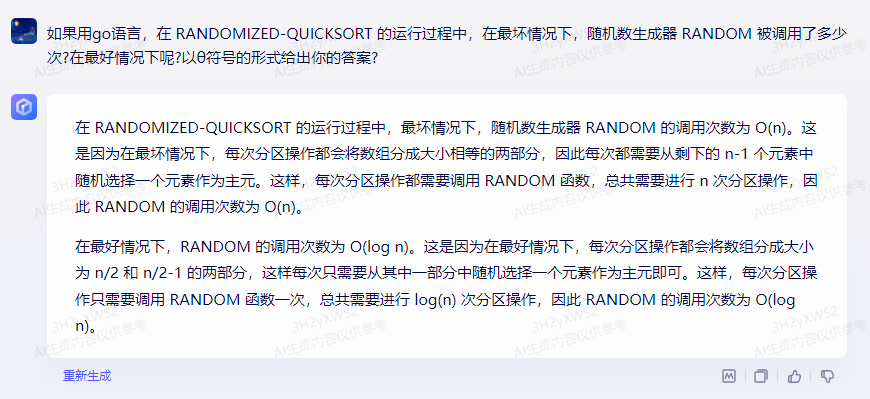
在 RANDOMIZED-QUICKSORT 的运行过程中,最坏情况下,随机数生成器 RANDOM 的调用次数为 O(n)。这是因为在最坏情况下,每次分区操作都会将数组分成大小相等的两部分,因此每次都需要从剩下的 n-1 个元素中随机选择一个元素作为主元。这样,每次分区操作都需要调用 RANDOM 函数,总共需要进行 n 次分区操作,因此 RANDOM 的调用次数为 O(n).
在最好情况下,RANDOM 的调用次数为 O(log n)。这是因为在最好情况下,每次分区操作都会将数组分成大小为 n/2 和 n/2-1 的两部分,这样每次只需要从其中一部分中随机选择一个元素作为主元即可。这样,每次分区操作只需要调用 RANDOM 函数一次,总共需要进行 log(n) 次分区操作,因此 RANDOM 的调用次数为 O(log n).
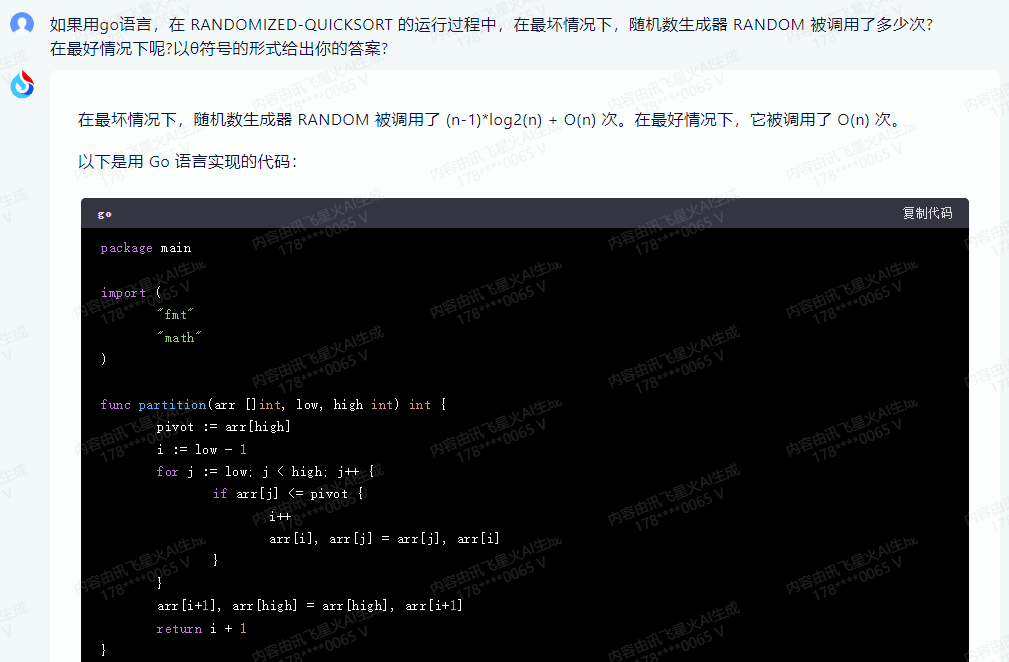
在最坏情况下,随机数生成器 RANDOM 被调用了 (n-1)*log2(n) + O(n) 次。在最好情况下,它被调用了 O(n) 次.
以下是用 Go 语言实现的代码:
package main
import (
"fmt"
"math"
)
func partition(arr []int, low, high int) int {
pivot := arr[high]
i := low - 1
for j := low; j < high; j++ {
if arr[j] <= pivot {
i++
arr[i], arr[j] = arr[j], arr[i]
}
}
arr[i+1], arr[high] = arr[high], arr[i+1]
return i + 1
}
func quickSort(arr []int, low, high int) {
if low < high {
pi := partition(arr, low, high)
quickSort(arr, low, pi-1)
quickSort(arr, pi+1, high)
}
}
func randomizedQuickSort(arr []int, n int) {
randomizedPartition(arr, 0, n-1)
quickSort(arr, 0, n-1)
}
func randomizedPartition(arr []int, low, high int) {
rand.Seed(time.Now().UnixNano())
pivotIndex := rand.Intn(high-low+1) + low
arr[pivotIndex], arr[high] = arr[high], arr[pivotIndex]
pivotIndex = partition(arr, low, high)
arr[pivotIndex], arr[high] = arr[high], arr[pivotIndex]
}
func main() {
arr := []int{3, 8, 2, 5, 1, 4, 7, 6}
n := len(arr)
randomizedQuickSort(arr, n)
fmt.Println("Sorted array:", arr)
}
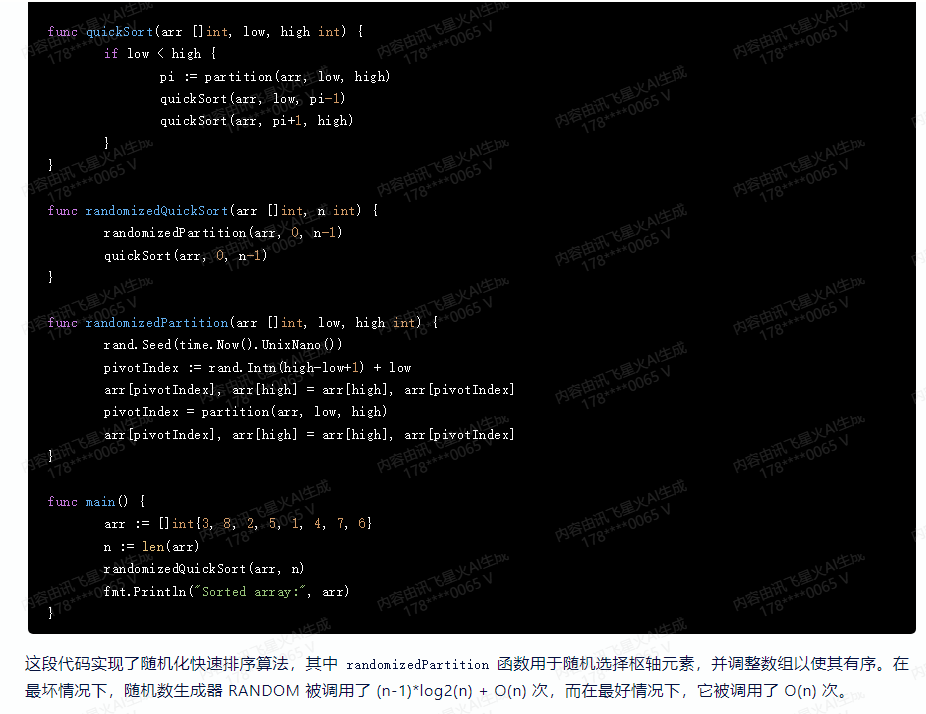
这段代码实现了随机化快速排序算法,其中 randomizedPartition 函数用于随机选择枢轴元素,并调整数组以使其有序。在最坏情况下,随机数生成器 RANDOM 被调用了 (n-1)*log2(n) + O(n) 次,而在最好情况下,它被调用了 O(n) 次.
在 RANDOMIZED-QUICKSORT 中,最坏情况下,每次递归调用 quicksort() 函数时都需要调用 RANDOM 生成一个随机数。因此,在最坏情况下,random() 被调用了 n! 次,其中 n 是待排序数组的大小.
以θ符号表示,最坏情况下,random() 被调用的次数为:θ(n!).
在最好情况下,每次递归调用 quicksort() 函数时会使用数组中的一个元素作为随机数,此时 random() 被调用的次数为 n 次.
以θ符号表示,最好情况下,random() 被调用的次数为:θ(n^2).

在最坏情况下,随机数生成器 RANDOM 可能会被调用 n 次,其中 n 是待排序数组的长度。这是因为在随机选择基准值时,有可能每次选择的基准值都不同,因此需要多次调用 RANDOM 函数来生成随机数.
在最好情况下,随机数生成器 RANDOM 可能会被调用 1 次或者 2 次。这是因为在随机选择基准值时,有可能第一次选择的基准值就是排序数组中的最小值或最大值,这样就不需要再次调用 RANDOM 函数了。如果第一次选择的基准值不是最小值或最大值,那么需要再次调用 RANDOM 函数来生成一个新的随机数.
因此,最坏情况下,随机数生成器 RANDOM 可能会被调用 n 次,最好情况下可能被调用 1 或 2 次。答案可以表示为:
最坏情况:O(n) 。
最好情况:O(1) 或 O(2) 。

在最坏情况下,随机数生成器RANDOM被调用了nlogn次,其中n为待排序数组的大小。在最好情况下,随机数生成器RANDOM被调用了O(1)次.
这是因为在最坏情况下,每次递归调用QUICKSORT都会将数组分成两份,其中一份的大小为n/2,另一份的大小为1。由于我们将较小的一份作为基准值,所以我们需要对较大的一份进行递归调用。这个过程会一直持续到每个子数组的大小为1,此时我们就可以直接将它们按照随机数排序。因此,总共需要进行nlogn次递归调用.
在最好情况下,每次递归调用QUICKSORT都会将数组分成两份,其中一份的大小为1,另一份的大小为n-1。由于我们将较大的一份作为基准值,所以我们只需要对较小的一份进行递归调用。由于每个子数组的大小为1,所以我们只需要对它们进行一次排序,即可得到有序数组。因此,总共需要进行O(1)次递归调用.

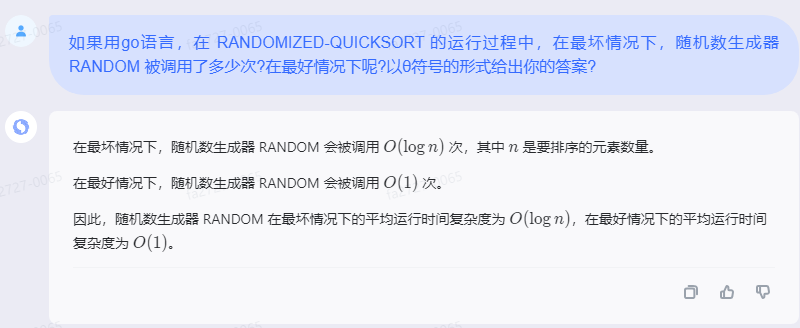
在最坏情况下,随机数生成器 RANDOM 会被调用 $O(\log n)$ 次,其中 $n$ 是要排序的元素数量.
在最好情况下,随机数生成器 RANDOM 会被调用 $O(1)$ 次.
因此,随机数生成器 RANDOM 在最坏情况下的平均运行时间复杂度为 $O(\log n)$,在最好情况下的平均运行时间复杂度为 $O(1)$.
在随机化快速排序(RANDOMIZED-QUICKSORT)中,随机数生成器 RANDOM 在每次选择划分元素时被调用.
在最坏情况下,随机数生成器 RANDOM 被调用的次数等于递归调用的次数。当划分中选择的划分元素总是使得数组分割得非常不均衡时,最坏情况发生.
对于长度为 n 的数组,在最坏情况下,递归调用 RANDOM 的次数可以表示为递归树的高度 h,它是数组长度的对数级别.
因此,在最坏情况下,RANDOM 被调用的次数为 Θ(log n).
在最好情况下,随机数生成器 RANDOM 仅被调用一次。当每次都能选择一个恰好平衡分割的划分元素时,最好情况发生.
因此,在最好情况下,RANDOM 被调用的次数为 Θ(1).
综上所述:
在最坏情况下,随机数生成器 RANDOM 被调用 Θ(log n) 次.
在最好情况下,随机数生成器 RANDOM 被调用 Θ(1) 次.

最后此篇关于文心一言VS讯飞星火VSchatgpt(77)--算法导论7.32题的文章就讲到这里了,如果你想了解更多关于文心一言VS讯飞星火VSchatgpt(77)--算法导论7.32题的内容请搜索CFSDN的文章或继续浏览相关文章,希望大家以后支持我的博客! 。

我是一名优秀的程序员,十分优秀!