- Java锁的逻辑(结合对象头和ObjectMonitor)
- 还在用饼状图?来瞧瞧这些炫酷的百分比可视化新图形(附代码实现)⛵
- 自动注册实体类到EntityFrameworkCore上下文,并适配ABP及ABPVNext
- 基于Sklearn机器学习代码实战
图像识别技术是信息时代的一门重要的技术,其产生目的是为了让计算机代替人类去处理大量的物理信息。传统图像识别技术的过程分为信息的获取、预处理、特征抽取和选择、分类器设计和分类决策。本文也是从这四点出发进行行文,以期了解传统图像识别技术、掌握hog特征提取和svm分类器。 笔者的运行环境:python3.7+pycharm+opencv4.6,全文代码均可运行.
简单理解就是把一幅图像转换成适合输入计算机和数字设备的数字信号。这需要要两个部件以获取数字图像:
常见的图像输入设备有:扫描仪、摄像机、数码相机、图像采集卡等.
图像预处理的主要目的是消除图像中无关的信息,恢复有用的真实信息,增强有关信息的可检测性和最大限度地简化数据,从而改进特征抽取、图像分割、匹配和识别的可靠性。 图像预处理的一般步骤为:灰度化-->几何变换-->图像增强,在具体项目中根据需要进行灵活运用.
灰度化是将图像转变成灰度图像,一般有分量法、最大值法、平均值法、加权平均法等.
表述:图像的灰度值可以是RGB三通道中的任意一通道的亮度值,也就是说可以将图像的R通道值作为灰度值,也可以是G通道或B通道。 数学表达:F(x, y) = R(x, y)或F(x, y) = G(x, y)或F(x, y) = B(x, y) OpenCv中复现:
def image_gray1(img):
# 分量法灰度化图像
# 判断输入图像是否为灰度图
if len(img.shape) > 2:
b, g, r = img[:, :, 0], img[:, :, 1], img[:, :, 2]
gray = b # B通道值作为灰度值
gray = g # G通道值作为灰度值
gray = r # R通道值作为灰度值
return gray
else:
return img
表述:取图像中(x, y)位置像素的RGB通道中的最大值为灰度值。 数学表达:F(x, y) = max(R(x, y), G(x, y), B(x, y)) OpenCv中复现:
def image_gray2(img):
# 最大值法灰度化图像
grayimg = np.zeros(shape=(img.shape[0],img.shape[1]))
if len(img.shape) > 2:
for i in range(img.shape[0]):
for j in range(img.shape[1]):
grayimg[i,j] = max(img[i,j][0], img[i,j][1], img[i,j][2])
return grayimg
else:
return img
表述:图像中每个像素的灰度值是其原图像三通道值得平均值。 数学表达:F(x, y) = (R(x, y) + G(x, y) + B(x, y)) / 3 OpenCv中复现:
def image_gray3(img):
# 平均值法灰度化图像
grayimg = np.zeros(shape=(img.shape[0], img.shape[1]))
if len(img.shape) > 2:
for i in range(img.shape[0]):
for j in range(img.shape[1]):
grayimg[i, j] = (int(img[i, j][0])+int(img[i, j][1])+int(img[i, j][2]))/3
return grayimg
else:
return img
表述:每个通道都有加权系数,根据系数计算其加权平均值。 数学表达:F(x, y) = 0.2989R(x, y)+0.5870G(x, y)+0.1140B(x, y) OpenCv中复现:
def convert2gray(img):
# 加权平均分灰度化图像
if len(img.shape) > 2:
r, g, b = img[:, :, 0], img[:, :, 1], img[:, :, 2]
gray = 0.2989 * r + 0.5870 * g + 0.1140 * b
return gray
else:
return img
opencv中内置了两个函数对图像灰度化,即c v2.imread(filaname, cv2.IMREAD_GRAYSCALE) 和 cv2.cvColor(src, code[, dst[, dstCn]]) (转换为灰度图时 code = cv2.COLOR_BGR2GRAY ).
图像几何变换又称为图像空间变换,通过平移、转置、镜像、旋转、缩放等几何变换对采集的图像进行处理,用于改正图像采集系统的系统误差和仪器位置(成像角度、透视关系乃至镜头自身原因)的随机误差。此外,还需要使用灰度插值算法,因为按照这种变换关系进行计算,输出图像的像素可能被映射到输入图像的非整数坐标上。通常采用的方法有最近邻插值、双线性插值和双三次插值。 opencv中的几何变换可见 这里 .
增强图像中的有用信息,它可以是一个失真的过程,其目的是要改善图像的视觉效果,针对给定图像的应用场合,有目的地强调图像的整体或局部特性,将原来不清晰的图像变得清晰或强调某些感兴趣的特征,扩大图像中不同物体特征之间的差别,抑制不感兴趣的特征,使之改善图像质量、丰富信息量,加强图像判读和识别效果,满足某些特殊分析的需要。 图像增强可分成两大类:频率域法和空间域法.
频率域法把图像看成一种二维信号,对其进行基于二维傅里叶变换的信号增强。 高频图像是指强度变化很多的图像,亮度水平从一个像素到另一个像素变化很快。低频图像可能是亮度比较均匀或变化很慢的图像。 频率域法是一种间接图像增强算法,把图像看成一种二维信号,对其进行基于二维傅里叶变换的信号增强。采用低通滤波(即只让低频信号通过)法,可去掉图中的噪声;采用高通滤波法,则可增强边缘等高频信号,使模糊的图片变得清晰。 opencv中频率域图像滤波的有关算法见: https://youcans.blog.csdn.net/article/details/125112487#6__103 。
空间域图像增强技术指在空间域中,通过线性和非线性变换来增强构成图像的像素 增强的方法主要分为点运算算法、形态学运算法、邻域增强算法。 点运算法 点运算算法即灰度级校正、灰度变换(伽马变换、对数增强)和直方图修正等,目的或使图像成像均匀,或扩大图像动态范围,扩展对比度。 opencv中灰度变换与直方图见: 【youcans的OpenCV例程300篇】总目录_youcans_的博客-CSDN博客 形态学运算法 图像处理中的形态学是指基于形状的图像处理操作,以数学形态学为工具从图像中提取表达和描绘区域形状的图像结构信息,还包括用于预处理或后处理的形态学过滤、细化和修剪等。 opencv中形态学图像处理见: 【youcans的OpenCV例程300篇】总目录_youcans_的博客-CSDN博客 邻域增强算法 邻域增强算法分为图像平滑和锐化两种。平滑一般用于消除图像噪声,但是也容易引起边缘的模糊。常用算法有均值滤波、中值滤波。锐化的目的在于突出物体的边缘轮廓,便于目标识别。锐化常用算法有梯度法(如Roberts梯度法)、算子法(Sobel算子和拉普拉斯算子等)、掩模匹配法、统计差值法等常用算法有梯度法、算子、高通滤波、掩模匹配法、统计差值法等。 opencv中空间域图像滤波见: 【youcans的OpenCV例程300篇】总目录_youcans_的博客-CSDN博客 。
特征提取的英文叫做feature extractor,它是将一些原始的输入的数据维度减少或者将原始的特征进行重新组合以便于后续的使用。简单来说有两个作用:减少数据维度,整理已有的数据特征.
Haar、Gabor、LBP、SIFI、HOG、SURF等算法.
| |
Haar | Gabor | LBP |
|---|---|---|---|
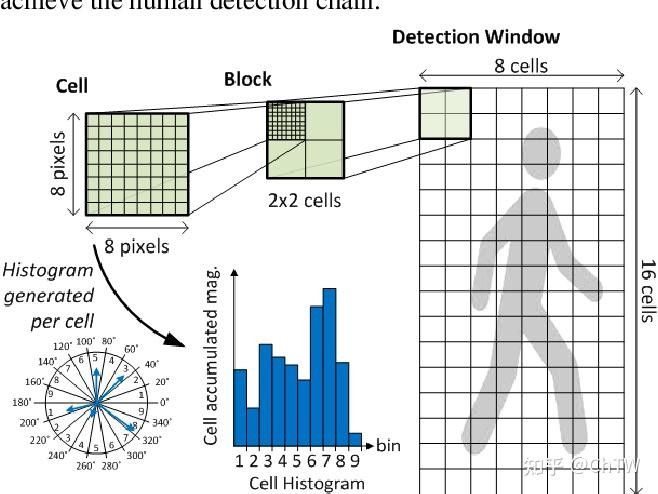
| 概述 | Haar特征通常被用来检测图像中的局部特征,如边缘、线和角等。Haar特征是通过在图像中滑动一个固定大小的窗口,并计算窗口内像素的灰度差异来确定的。这些特征通常由矩形区域的亮度差异组成,其中矩形区域可以是水平、竖直或对角线方向的。 | 在计算机视觉中,Gabor滤波器通常被用来检测图像中的纹理和边缘等特征。它可以通过在图像上滑动一个Gabor核来提取特定方向、尺度和频率的特征,从而生成滤波响应图像。Gabor滤波器的参数包括中心频率、方向、尺度和带宽等。 | LBP(Local Binary Pattern,局部二值模式)是一种用于图像分析和计算机视觉的特征描述符。它可以对图像中的纹理和结构进行描述,并且非常适合于目标检测、人脸识别、纹理分类等应用。 |
| 优点 | 简单有效、不受光照影响、不受目标大小变化影响、鲁棒性好、可以结合其他方法使用 | 较好的方向选择性、尺度不变性、可以提取细节信息、可以结合其他方法使用 | 计算简单、不受光照变化影响、可以处理局部纹理特征、可以与其他方法结合 |
| 缺点 | 对目标旋转敏感、计算复杂度高、只适用于灰度图像、对目标变形敏感 | 计算复杂度高、对图像噪声敏感、对光照变化敏感、参数选择困难 | 对噪声敏感、不具备旋转不变性、不能描述全局纹理信息 |
| 应用场景 | 人脸、人眼检测,车牌检测 | 纹理分析、人脸识别、指纹识别、目标检测 | 图形分类目标检测、人脸识别 |
| |
SIFT | HOG | SURF |
|---|---|---|---|
| 概述 | SIFT(Scale-Invariant Feature Transform:尺度不变特性变换)是一种在计算机视觉领域中广泛应用的特征提取算法。它能够在不同的尺度和旋转角度下提取出图像中的关键点,并计算出这些关键点的局部特征描述子,从而实现图像的匹配和识别。 | HOG(Histograms of Oriented Gradients:定向梯度直方图)是一种基于图像梯度的特征提取方法,被广泛应用于计算机视觉和机器学习领域 | SURF(Speeded Up Robust Features)是一种用于图像特征提取和匹配的算法,它是 SIFT(Scale-Invariant Feature Transform)算法的改进版本。SURF 算法通过快速的图像特征提取和匹配,可以在大规模图像数据集上实现高效的识别和匹配。 |
| 优点 | 较好的尺度不变性、旋转不变性、抗噪性能、匹配准确性 | 较好的局部特征、光照不变性、计算效率、可扩展性 | 计算速度快、尺度不变性和旋转不变性、鲁棒性好、可扩展 |
| 缺点 | 计算量大、对图像畸变敏感、对亮度变化敏感、不适用于快速移动目标 | 对目标旋转和缩放不具有完全的不变性、对图像噪声敏感、不适用于高速运动目标 | 对旋转和仿射变换的鲁棒性不如其他算法、对光照变化和噪声敏感、特征点数量不稳定 |
| 应用场景 | 图像匹配和识别,例如目标跟踪、三维重建、图像检索等 | 人脸检测、行人检测、车辆检测、图像分类,单目标跟踪 | 目标检测、图像拼接、三维重建、相机定位、视频跟踪 |
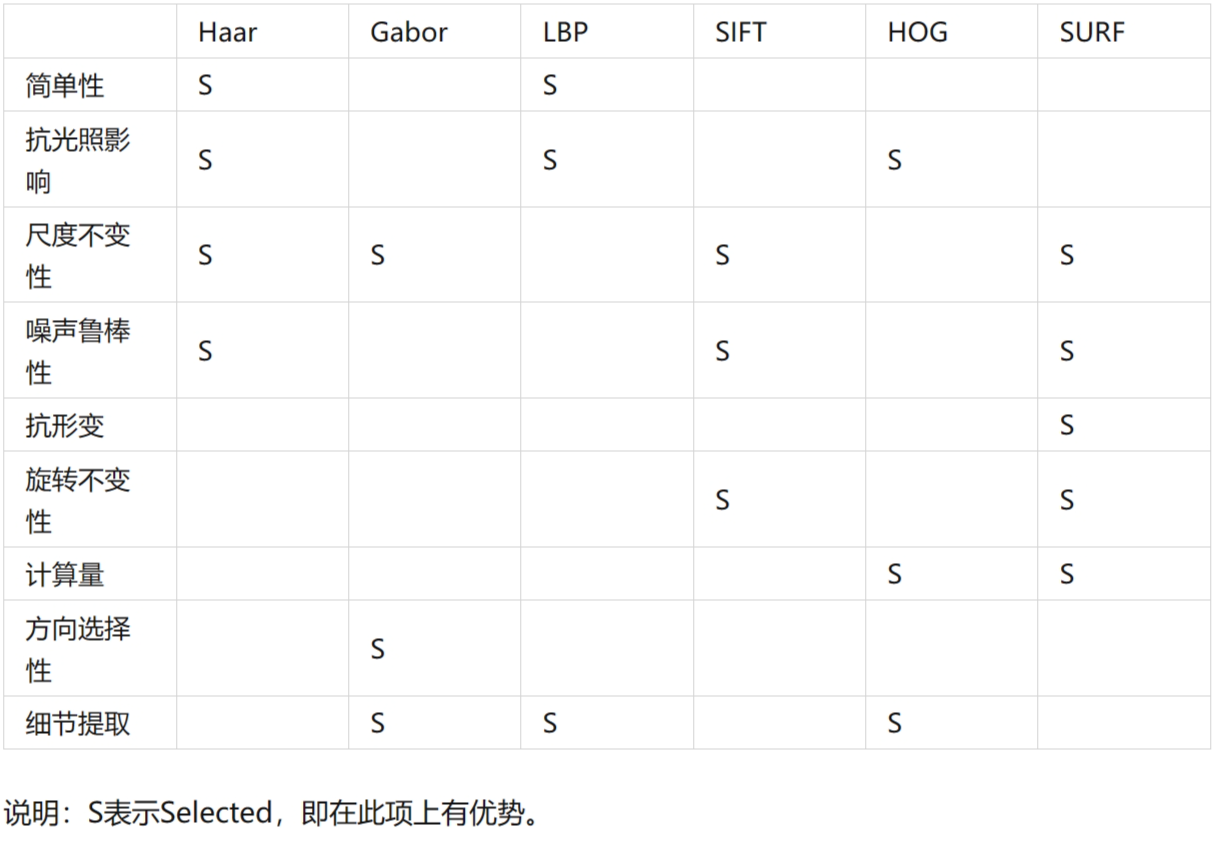
特征描述符是通过提取图像的有用信息,并且丢弃无关信息来简化图像的表示。 HOG特征描述符可以将3通道的彩色图像或者单通道的灰度图转换成一定长度的特征向量。而且HOG描述符多和SVM配合使用,用于训练高精度的目标分类器.
关于特征值和特征向量: 我们知道,一个变换可由一个矩阵乘法表示,那么一个空间坐标系也可视作一个矩阵,而这个坐标系就可由这个矩阵的所有特征向量表示,用图来表示的话,可以想象就是一个空间张开的各个坐标角度,这一组向量可以完全表示一个矩阵表示的空间的“特征”,而他们的特征值就表示了各个角度上的能量(可以想象成从各个角度上伸出的长短,越长的轴就越可以代表这个空间,它的“特征”就越强,或者说显性,而短轴自然就成了隐性特征),因此,通过特征向量/值可以完全描述某一几何空间这一特点,使得特征向量与特征值在几何(特别是空间几何)及其应用中得以发挥.
此方法的基本观点是:局部目标的外表和形状可以被局部梯度或边缘方向的分布很好的描述,即使我们不知道对应的梯度和边缘的位置。(本质:梯度的统计信息,梯度主要存在于边缘的地方) 。
首先,将图像分成很多小的连通区域,我们把它叫做cell,然后采集cell中各像素点的梯度大小和方向,在每个cell中通过某种方式绘制一个一维的梯度方向直方图。 其次,为了对光照和阴影有更好的不变性,需要对直方图进行对比度归一化,这可以通过把这些直方图在图像的更大的范围内(我们把它叫做区间或者block)进行对比度归一化。我们把归一化的块描述符叫作HOG描述子.
Gamma校正公式为: f(I)=Iγ 其中I为图像像素值,γ为Gamma校正系数。γ系数设定影响着图像的调整效果,结合下图,我们来看一下Gamma校正的作用: γ<1在低灰度值区域内,动态范围变大,图像对比度增加强;在高灰度值区域,动态范围变小,图像对比度降低,同时,图像的整体灰度值变大; γ>1在低灰度值区域内,动态范围变小,图像对比度降低;在高灰度值区域,动态范围变大,图像对比度提高,同时,图像的整体灰度值变小; 左边的图像为原图,中间图像的γ=12.2,右图γ=2.2。 作者在他的博士论文里有提到,对于涉及大量的类内颜色变化,如猫,狗和马等动物,没标准化的RGB图效果更好,而牛,羊的图做gamma颜色校正后效果更好。是否用gamma校正需要分析具体的训练集情况.
像素点的幅值和幅度 首先,利用中心差分近似计算每个像素点对x、y的偏导: Gx(x,y)=I(x+1,y)−I(x−1,y) Gy(x,y)=I(x,y+1)−I(x,y−1) 上式中Gx(x,y)、Gy(x,y)分别表示输入图像在像素点(x,y)处的水平方向梯度和垂直方向梯度,该点处的幅值和幅度为: G(x, y) = √Gx(x, y)2+Gy(x, y)2 α = arctan(Gy(x,y)/Gx(x,y)) cell梯度直方图 为什么要将图像按cell尺寸分割呢?将图像分成cell单元是为了可以用多个cell组合成block,通过block获得较好的特征和抗光照影响。 我们先把整个图像划分为若干个8x8的小单元,称为cell,并计算每个cell的梯度直方图。这个cell的尺寸也可以是其他值,根据具体的特征而定。一个8x8的cell包含了8 8 2=128个值,因为每个像素包括梯度的大小和方向。 将cell单元中的幅度作为横轴,幅度对应像素点的幅度的累加值作为相应纵轴值,组成一个梯度直方图。论文作者,将幅度分成9份取得了较为理想的行人检测效果。我们将横轴的角度分成9份,也就是9个bins,每20°为一份(有符号角度是40°为一份),横轴坐标为0, 20, 40, ..., 160。那么横轴值对应的纵轴值该如何计算呢,我们用一个例子来学习: 比如上面方向图中蓝圈包围的像素,角度为80度,这个像素对应的幅值为2,所以在直方图80度对应的bin加上2。红圈包围的像素,角度为10度,介于0度和20度之间,其幅值为4,那么这个梯度值就被按比例分给0度和20度对应的bin,也就是各加上2。 还有一个细节需要注意,如果某个像素的梯度角度大于160度,也就是在160度到180度之间,那么把这个像素对应的梯度值按比例分给0度和160度对应的bin。将这 8x8 的cell中所有像素的梯度值加到各自角度对应的bin中,就形成了长度为9的直方图: 可以看到直方图中,0度和160附近有很大的权重,说明了大多数像素的梯度向上或者向下,也就是这个cell是个横向边缘。现在我们就可以用这9个数的梯度直方图来代替原来很大的三维矩阵,即代替了8x8x2个值.
于局部光照的变化,以及前景背景对比度的变化,使得梯度强度的变化范围非常大,这就需要对梯度做局部对比度归一化。归一化能够进一步对光照、阴影、边缘进行压缩,使得特征向量对光照、阴影和边缘变化具有鲁棒性。 具体的做法:将细胞单元组成更大的空间块(block),然后针对每个块进行对比度归一化。最终的描述子是检测窗口内所有块内的细胞单元的直方图构成的向量。事实上,块之间是有重叠的,也就是说,每个细胞单元的直方图都会被多次用于最终的描述子的计算。块之间的重叠看起来有冗余,但可以显著的提升性能 。如下动图所示。 如上图所示,每个block由2×2个cell组成,每一个cell包含8×8个像素点,每个cell提取9个直方图通道,因此一个块的特征向量长度为2×2×9=36。 假设v是未经归一化的特征向量。||v||k是v的k范数,k=1,2,对块的特征向量进行归一化,一般有以下四种方法: 在人体检测系统中进行HOG计算时一般使用L2−norm,Dalal的文章也验证了对于人体检测系统使用L2−norm的时候效果最好.
最后一步就是对一个样本中所有的块进行HOG特征的提取,并将它们结合成最终的特征向量送入分类器。 那么一个样本可以提取多少个特征呢?之前我们已经说过HOG特征的提取过程:
例如:对于128×64128×64的输入图片(后面我所有提到的图像大小指的是h×w),每个块由2×2个cell组成,每个cell由8×8个像素点组成,每个cell提取9个bin大小的直方图,以1个cell大小为步长,那么水平方向有15个扫描窗口,垂直方向有7个扫描窗口,也就是说,一共有15∗7∗2∗2∗9=3780个特征.
opencv中没有提供简单的方法可视化HOG描述符,因此这里使用 scikit-image 库。先让我们来了解一下 feature.hog() 函数。 语法 :feature.hog(image, orientations=9, pixels_per_cell=(8, 8), cells_per_block=(3, 3), visualize=False, multichannel=None)--->fd, hog_image 参数 : orientations---要创建的bucket的数量,默认为9。 pixels_per_cell---单元格的大小,默认为8。可以简单理解为与HOG的信息紧凑性、抗噪声性能有关。 cells_per_block---Block的大小,单位是cell。可以简单理解与HOG的抗光照能力有关。 visualize---True,表示输出hog_image;False,表示不输出hog_image。 multichannel---None,表示输入的是单通道;True,可以输入多通道图。 返回 :fd---函数的特征矩阵;hog_image---HOG描述符图像.
import cv2
import numpy as np
from skimage import feature, exposure
runner = cv2.imread('image\\runner.jpg', cv2.IMREAD_COLOR)
# 将图像尺寸调整为64*128
runner_copy = cv2.resize(runner, dsize=(200, 400))
fd, hog_image = feature.hog(runner_copy, orientations=9, pixels_per_cell=(10, 10),
cells_per_block=(2, 2), visualize=True, multichannel=True)
# 重新缩放直方图以获得更好的显示效果
hog_image_rescaled = exposure.rescale_intensity(hog_image, in_range=(0, 10))
combined = np.hstack((hog_image, hog_image_rescaled))
cv2.imshow('11', combined)
while 1:
if cv2.waitKey(0) == ord('q'):
break
cv2.destroyAllWindows()

语法 : hog=cv2.HOGDescriptor(winSize, blocSize, blockStride, cellSize, nbins, derivAperture, winSigma, histogramNormType, L2HysThreshold, gammaCorrection, nlevels, signedGradients) 参数 : winSize---检测窗口大小。 blockStride---块步幅确定相邻块之间的重叠并控制对比度归一化程度。通常,块步幅设置为块大小的 50%。 blockSize---block是为了是为了抗光照影响而设计的。较大的块使局部图像的梯度直方图作用减弱,而较小的块则使局部图像的权重较大。通常,blockSize 设置为 2 x cellSize cellSize---单元格的大小,直接影响图像特征向量的大小。非常小的单元格会放大特征向量的大小,而非常大的单元格可能无法捕获相关信息。因此cellSize十分重要,应通过比较确定。 nbins---方向梯度直方图的条目数,积将梯度方向角度范围均分的份数,HOG论文的作者建议值为9。 signedGradients---True,有符号梯度,梯度方向角度范围[0, 360];False---无符号梯度,梯度方向角度范围[0, 180]。在最初的HOG论文中,无符号梯度用于行人检测。 检测器的函数方法: checkDetectorSize()---检查检测器大小是否等于描述符大小。 compute(img)---计算输入图像的特征向量。 --->descriptors computeGradient(img, grad, angleOfs)---计算梯度和量化梯度方向.--->grad, angleOfs detect(img)---在没有多尺度窗口的情况下执行对象检测。 --->foundLocations, weights detectMultiScale(img)---检测输入图像中不同尺度大小的对象。检测到的对象以矩形列表的形式返回。 --->foundLocations, foundWeights getDescriptorSize()---获取检测窗口的HOG特征向量的维数。 --->retcal getWinSigma()---返回 winSigma 值。 --->retcal load(filename[, objname])--- save(filename[, objname])---将线性 SVM 分类器的 HOGDescriptor 参数和系数保存到文件中。 --->None 。
def get_hog():
winSize = (20, 20)
blockSize = (8, 8)
blockStride = (4, 4)
cellSize = (8, 8)
nbins = 9
derivAperture = 1 # 默认参数
winSigma = -1. # 默认参数
histogramNormType = 0 # 默认参数
L2HysThreshold = 0.2 # 默认参数
gammaCorrection = 1 # 默认参数
nlevels = 64 # 默认参数
signedGradient = True
hog = cv2.HOGDescriptor(winSize, blockSize, blockStride, cellSize, nbins, derivAperture, winSigma,
histogramNormType, L2HysThreshold, gammaCorrection, nlevels, signedGradient)
return hog
图像分类(Image Classification)是对图像内容进行分类的问题,它利用计算机对图像进行定量分析,把图像或图像中的区域划分为若干个类别,以代替人的视觉判断。图像分类的传统方法是特征描述及检测,这类传统方法可能对于一些简单的图像分类是有效的.
常见的分类算法包括朴素贝叶斯分类器、决策树、K最近邻分类算法、支持向量机、神经网络和基于规则的分类算法等,同时还有用于组合单一类方法的集成学习算法,如Bagging和Boosting等.
| |
概述 | 特点 |
|---|---|---|
| 朴素贝叶斯分类算法 (Naive Bayes Classifier) |
发源于古典数学理论,利用Bayes定理来预测一个未知类别的样本属于各个类别的可能性,选择其中可能性最大的一个类别作为该样本的最终类别。在朴素贝叶斯分类模型中,它将为每一个类别的特征向量建立服从正态分布的函数,给定训练数据,算法将会估计每一个类别的向量均值和方差矩阵,然后根据这些进行预测。 | 如果没有很多数据,该模型会比很多复杂的模型获得更好的性能,因为复杂的模型用了太多假设,以致产生欠拟合。 |
| KNN分类算法(K-Nearest Neighbor Classifier) | 是一种基于实例的分类方法,是数据挖掘分类技术中最简单常用的方法之一。该算法的核心思想如下:一个样本x与样本集中的k个最相邻的样本中的大多数属于某一个类别yLabel,那么该样本x也属于类别yLabel,并具有这个类别样本的特性。 | 简单有效,但因为需要存储所有的训练集,占用很大内存,速度相对较慢,使用该方法前通常训练集需要进行降维处理。 |
| SVM分类算法(Support Vector Machine) | 根据统计学习理论提出的一种新的学习方法,其基本模型定义为特征空间上间隔最大的线性分类器,其学习策略是间隔最大化,最终转换为一个凸二次规划问题的求解。SVM基于核函数把特征向量映射到高维空间,建立一个线性判别函数,解最优在某种意义上是两类中距离分割面最近的特征向量和分割面的距离最大化。离分割面最近的特征向量被称为“支持向量”,即其它向量不影响分割面。图像分类中的SVM如下图所示,将图像划分为不同类别。 | 当数据集比较小的时候,支持向量机的效果非常好。同时,SVM分类算法较好地解决了非线性、高维数、局部极小点等问题,维数大于样本数时仍然有效。 |
| 随机森林分类算法(Random Forest) | 是用随机的方式建立一个森林,在森林里有很多决策树的组成,并且每一棵决策树之间是没有关联的。当有一个新样本出现的时候,通过森林中的每一棵决策树分别进行判断,看看这个样本属于哪一类,然后用投票的方式,决定哪一类被选择的多,并作为最终的分类结果。 | 在分类和回归分析中都表现良好;对高维数据的处理能力强,可以处理成千上万的输入变量,也是一个非常不错的降维方法;能够输出特征的重要程度,能有效地处理缺省值。 |
支持向量机通俗导论(理解SVM的三层境界)_v_JULY_v的博客-CSDN博客 。
opencv中集成了基于LIBSVM实现的SVM接口,便于直接进行调用。在opencv中训练完模型后,可将SVM模型保存为xml文件,可以在实时性应用中通过C++接口调用参数文件,进行实时推断。 SVM继承自StatModel和Algorithm类。在opencv中使用SVM的一般流程如下:
语法:cv2.ml.SVM_create()--->retval 作用:创建一个空模型.
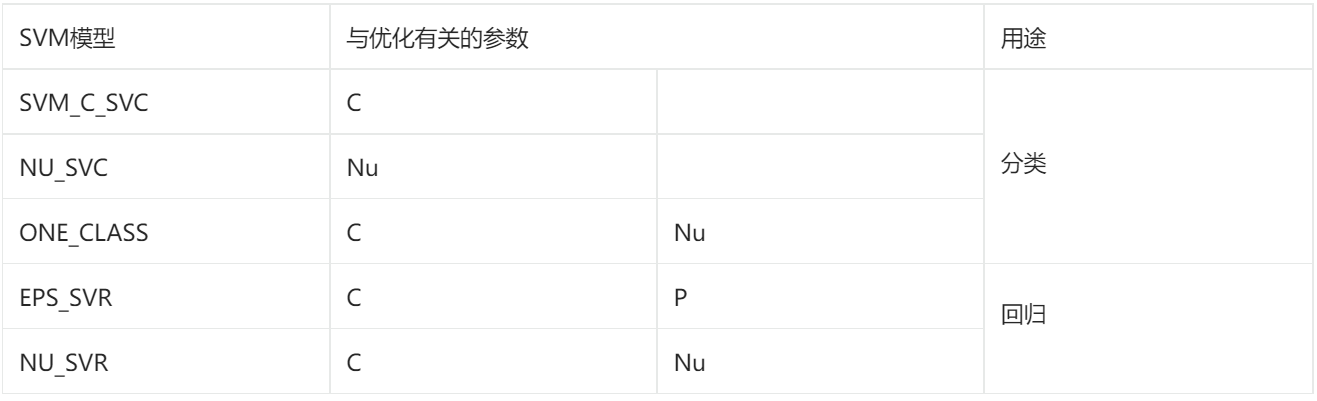
| SVM核函数 | 核函数表达式 | 与核函数有关的参数 | ||
|---|---|---|---|---|
| SVM_LINEAR (线性内核) |  |
|||
| SVM_POLY (多项式内核) | 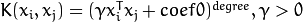 |
Gamma(γ>0) | Coef0 | Degree |
| SVM_RBF (径向基内核) | 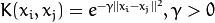 |
Gamma(γ>0) | ||
| SVM_SIGMOID (sigmoid内核) | 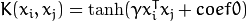 |
Gamma(γ>0) | Coef0 | |
| SVM_CHI2 (指数卡方分布内核) | k(xi, xj) = exp(γxiTxj+cofe0) | Gamma(γ>0) | |
|
| SVM_INTER (直方图交运算内核) | k(xi, xj) = min(xi, xj) | |
|
表格参考自: SVM参数设置总结(参考源码ml.hpp) - 夕西行 - 博客园 。
setType(val)---> None val = cv2.ml.SVM_C_SVC ,即数100。C-支持向量分类。n级分类(n≥ 2) 允许使用异常值的惩罚乘数 C 不完全地分离类。 val = cv2.ml.SVM_NU_SVC ,即数101。ν-支持向量分类。n级分类,可能有不完美的分离。参数ν用于代替C,参数ν在0-1范围内,值越大,决策边界越平滑。 val = cv2.ml.SVM_ONE_CLASS ,即数102。分布估计,所有的训练数据都来自同一个类,SVM 构建了一个边界,将类与特征空间的其余部分分开。 val = cv2.ml.SVM_EPS_SVR ,即数103。ε-支持向量回归。来自训练集的特征向量和拟合超平面之间的距离必须小于p。对于异常值,使用惩罚乘数 C。 val = cv2.ml.SVM_NU_SVR ,即数104。ν-支持向量回归。 ν用于代替 p。 补充: SVM=Support Vector Machine 是支持向量 SVC=Support Vector Classification就是支持向量机用于分类 SVC=Support Vector Regression.就是支持向量机用于回归分析 。
setC(val)--->None C值较大时:误分类错误较少,但余量较小。这种情况下,侧重于寻找具有很少的误分类错误的超平面。 C值较小时:具有更大余量和更多分类错误。在这种情况下,更侧重于寻找具有大余量的超平面。 默认值为[0.1 500].
setP(val)---> None 默认为[0.01, 100].
setNu(val)---> None 默认为[0.01, 0.2].
setKernel(kernelType)---> None kernelType = cv2.ml.SVM_CUSTOM ,默认为-1。由SVM::getKernelType返回,默认是RBF。 kernelType = cv2.ml.SVM_LINEAR ,默认为0。线性内核,速度最快。 kernelType = cv2.ml.SVM_POLY ,默认为1。多项式核。 kernelType = cv2.ml.SVM_RBF ,默认为2。径向基函数(RBF),大多数情况下是个不错的选择。 kernelType = cv2.ml.SVM_SIGMOID ,默认为3。sigmoid核。 kernelType = cv2.ml.SVM_CHI2 ,默认为4。Chi2核,类似于RBF核。 kernelType = cv2.ml.SVM_INTER ,默认为5。直方图交叉核,速度较快.
setGamma(val)---> None 默认为[1e-5, 0.6].
setDegree(val)---> None 默认为[0.01, 4].
setCoef0(val)---> None 默认为[0.1, 300].
setClassWeights(val)---> None 。
setTermCriteria((type, maxCount, epsilon))---> None 参数: type---终止迭代的类型。 cv2.TERM_CRITERIA_MAX_ITER , cv2.TERM_CRITERIA_COUNT ,以最大迭代次数控制迭代终止; cv2.TERM_CRITERIA_EPS ,以迭代算法精度控制迭代终止。 maxCount---最大的迭代次数; epsilon---迭代算法所需要的精度.
语法: trainAuto(samples, layout, responses[, kFold[, Cgrid[, gammaGrid[, pGrid[, nuGrid[, coeffGrid[, degreeGrid[, balanced]]]]]]]])---> retval train(samples, layout, responses)---> retval 参数: samples---训练样本的特征向量集,是以矩阵形式输入的。 layout--- cv2.ml.ROW_SAMPLE ,表示每个训练样本是行向量; cv2.ml.COL_SAMPLE ,表示每个训练样本是列向量。 responses---与训练样本有关的响应(标签)向量。 kFold---k交叉验证,训练集会分成k个子集,从中选取一个用来测试,剩余k-1个用来训练。 balanced---如果设为True且是2-class分类问题,方法会自动创建更平衡的交叉验证子集,即子集中的类之间比例接近整个训练数据集中的比例.
语法: predict(samples[, results[, flags]]---> retval, results 参数: samples---测试样本的向量集,是以矩阵形式输入的。 注意:测试样本的结果标签存储在 result.ravel() 中.
calcError(data, test[, resp])---> retval, resp 。
save(filename)---> None 。
load(filepath) -> retval 。
import cv2
import numpy as np
import random
# 设置显示框
width = 512
height = 512
win = np.zeros((height, width, 3), dtype=np.uint8)
def training_data(training_sample, sep):
global win
# 自定义数据集
# 每个类别的训练样本数量
training_samples = training_sample
# 线性可分的样本比例
frac_linear_sep = sep
# 设置训练样本和标签
train_data = np.empty((training_samples * 2, 2), dtype=np.float32)
labels = np.empty((training_samples * 2, 1), dtype=np.int32)
# 随机数种子
random.seed(100)
# 线性可分的样板训练数量
linear_samples = int(frac_linear_sep * training_samples)
# 创建线性可分class1,class1内的点坐标x∈[0, 0.4*width), y∈[0, 512)
train_class = train_data[0:linear_samples, :]
# 定义点的x坐标
c = train_class[:, 0:1]
c[:] = np.random.uniform(0.0, 0.4 * width, c.shape)
# 定义点的y坐标
c = train_class[:, 1:2]
c[:] = np.random.uniform(0.0, height, c.shape)
# 创建线性可分class2,class2内的点坐标x∈[0.6, width), y∈[0, 512)
train_class = train_data[(training_samples * 2 - linear_samples):training_samples * 2, :]
# 定义点的x坐标
c = train_class[:, 0:1]
c[:] = np.random.uniform(0.6 * width, width, c.shape)
# 定义点的y坐标
c = train_class[:, 1:2]
c[:] = np.random.uniform(0.0, height, c.shape)
# 创建线性不可分class,class内的点坐标x∈[0.4*width, 0.6*width), y∈[0, 512)
train_class = train_data[linear_samples:(training_samples * 2 - linear_samples), :]
# 定义点的x坐标
c = train_class[:, 0:1]
c[:] = np.random.uniform(0.4 * width, 0.6 * width, c.shape)
# 定义点的y坐标
c = train_class[:, 1:2]
c[:] = np.random.uniform(0.0, height, c.shape)
# 创建class1与class2的标签
labels[0:training_samples, :] = 1
labels[training_samples:training_samples * 2, :] = 2
return train_data, labels
def SVM_Model():
# 创建一个参数已经定义的模型model
model = cv2.ml.SVM_create()
model.setType(cv2.ml.SVM_C_SVC)
model.setC(0.1)
model.setKernel(cv2.ml.SVM_LINEAR)
model.setTermCriteria((cv2.TERM_CRITERIA_MAX_ITER, int(1e7), 1e-6))
return model
def train_model(model, samples, layout, reponses):
# 训练SVM模型
model.train(samples, layout, reponses)
return model
def display_area(model, color1, color2):
global win
# 显示决策区域
for i in range(win.shape[0]):
for j in range(win.shape[1]):
sample_mat = np.matrix([[j, i]], dtype=np.float32)
response = model.predict(sample_mat)[1]
if response == 1:
win[i, j] = color1
else:
win[i, j] = color2
def display_class(model, train_data, color1, color2, training_samples):
global win
# 按类显示训练数据中的点
for i in range(training_samples):
px = train_data[i, 0]
py = train_data[i, 1]
cv2.circle(win, (int(px), int(py)), 3, color1, -1)
for i in range(training_samples, 2*training_samples):
px = train_data[i, 0]
py = train_data[i, 1]
cv2.circle(win, (int(px), int(py)), 3, color2, -1)
sv = model.getUncompressedSupportVectors()
for i in range(sv.shape[0]):
cv2.circle(win, (int(sv[i, 0]), int(sv[i, 1])), 6, (200, 200, 200), 2)
if __name__ == '__main__':
training_samples = 150
frac_linear_sep = 0.9
print('创建训练数据'.center(50, '-'))
train_data, labels = training_data(training_samples, frac_linear_sep)
print('创建SVM模型'.center(50, '-'))
svm_model = SVM_Model()
print('训练SVM模型'.center(50, '-'))
svm_model = train_model(svm_model, train_data, cv2.ml.ROW_SAMPLE, labels)
print('显示决策区域'.center(50, '-'))
display_area(svm_model, (112, 125, 247), (168, 159, 121))
print('按类显示训练数据中的点'.center(50, '-'))
display_class(svm_model, train_data, (52, 70, 244), (107, 100, 69), training_samples)
cv2.imshow('111', win)
while 1:
if cv2.waitKey(0) == ord('q'):
break
cv2.destroyAllWindows()
运行结果:
训练资源: 代码:
#!/usr/bin/env python
import cv2
import numpy as np
# 本地模块common
from common import clock, mosaic
SZ = 20
CLASS_N = 10
def split2d(img, cell_size, flatten=True):
"""
将图像按照cell_size尺寸分割,将分割后的数组放置在一个新数组中并返回
:param img: 将要被分割的图像
:param cell_size: 分割尺寸
:param flatten: 是否扁平化从的标志
:return: img分割后的图像数组集
"""
h, w = img.shape[:2]
sx, sy = cell_size
cells = []
# 按行切分输入的图像
for row in np.vsplit(img, h//sy):
cells.append(np.hsplit(row, w // sx))
# 将列表转换称数组,shape=(h//sy, w//sx, sy, sx)
cells = np.array(cells)
if flatten:
# 将数组cells转为三维数组,shape=((h//sy)*(w//sx), sy, sx),(h//sy)*(w//sx)是切割后的图像数量
cells = cells.reshape((-1, sy, sx))
return cells
# 建立训练资源库和标签组
def load_digits(fn):
"""
建立训练资源库和对应的标签组
:param fn:输入图片的位置
:return:分割后的图像集合以及对应的标签组
"""
digits_img = cv2.imread(fn, 0)
# 通过split2d()函数分割读取的图像
digits = split2d(digits_img, (SZ, SZ))
# 建立[0, 9]的整数类,对应手写数字,数量与len(digits)同
labels = np.repeat(np.arange(CLASS_N), len(digits) / CLASS_N)
return digits, labels
# 纠偏
def deskew(img):
"""
判断图像倾斜是否在[0,1e-2)之内,若在返回一个副本,否则返回一个经过错切的图像
:param img: 输入图像
:return: 返回一个在倾斜角度内的图像
"""
m = cv2.moments(img)
if abs(m['mu02']) < 1e-2:
return img.copy()
skew = m['mu11'] / m['mu02']
# 创建错切矩阵
M = np.float32([[1, skew, -0.5 * SZ * skew], [0, 1, 0]])
# 错切变换
img = cv2.warpAffine(img, M, (SZ, SZ), flags=cv2.WARP_INVERSE_MAP | cv2.INTER_LINEAR)
return img
def svmInit(C=12.5, gamma=0.50625):
"""
创建并配置SVM模型
:param C: 参数C
:param gamma: 参数Gamma
:return: 返回一个已经配置完参数的SVM模型
"""
# 创建一个空SVM模型
model = cv2.ml.SVM_create()
model.setGamma(gamma)
model.setC(C)
# SVM核为SVM_RBF,需要有对应的Gamma参数
model.setKernel(cv2.ml.SVM_RBF)
# SVM类型为SVM_C_SVC,需要有对应的C参数
model.setType(cv2.ml.SVM_C_SVC)
return model
def svmTrain(model, samples, responses):
"""
返回经过训练的模型
:param model: 将要被训练的模型
:param samples: 训练数据
:param responses: 数据对应的标签
:return: 返回经过训练的模型
"""
model.train(samples, cv2.ml.ROW_SAMPLE, responses)
return model
def svmPredict(model, samples):
"""
返回模型对测试数据的预测结果
:param model: 已经训练好的模型
:param samples: 测试用的图像的特征向量
:return: 返回模型对测试数据的预测结果
"""
return model.predict(samples)[1].ravel()
def svmEvaluate(model, digits, samples, labels):
"""
返回一个打乱了的测试数据集,其中预测错误的数据是红色的
:param model: 已经训练好的模型
:param digits: 测试用的数据
:param samples: 测试用的数据的特征向量
:param labels: 测试用的数据对应的标签
:return: 返回一个打乱了的测试数据集,其中预测错误的数据是红色的
"""
predictions = svmPredict(model, samples)
accuracy = (labels == predictions).mean()
print('预测准确率: %.2f %%' % (accuracy * 100))
confusion = np.zeros((10, 10), np.int32)
for i, j in zip(labels, predictions):
confusion[int(i), int(j)] += 1
print('confusion matrix:')
print(confusion)
print(sum(sum(confusion)))
vis = []
for img, flag in zip(digits, predictions == labels):
img = cv2.cvtColor(img, cv2.COLOR_GRAY2BGR)
if not flag:
img[..., :2] = 0
vis.append(img)
return mosaic(25, vis)
# 图像归一化
def preprocess_simple(digits):
return np.float32(digits).reshape(-1, SZ * SZ) / 255.0
def get_hog():
"""
:return: 返回一个获得HOG描述符的函数
"""
winSize = (20, 20)
blockSize = (8, 8)
blockStride = (4, 4)
cellSize = (8, 8)
nbins = 9
derivAperture = 1
winSigma = -1.
histogramNormType = 0
L2HysThreshold = 0.2
gammaCorrection = 1
nlevels = 64
signedGradient = True
hog = cv2.HOGDescriptor(winSize, blockSize, blockStride, cellSize, nbins, derivAperture, winSigma,
histogramNormType, L2HysThreshold, gammaCorrection, nlevels, signedGradient)
return hog
if __name__ == '__main__':
print('加载本地图片 ... ')
# 本地数据
digits, labels = load_digits("image\\digits.png")
print('打乱数据 ... ')
# 打乱数据
rand = np.random.RandomState(10)
shuffle = rand.permutation(len(digits))
digits, labels = digits[shuffle], labels[shuffle]
print('纠偏 ... ')
# 纠偏
digits_deskewed = list(map(deskew, digits))
print('定义HOG参数 ...')
# 定义HOG参数
hog = get_hog()
print('提取每张图片的HOG特征向量 ... ')
hog_descriptors = []
# 提取提取每张图像的特征向量,并添加到列表hog_descriptors
for img in digits_deskewed:
hog_descriptors.append(hog.compute(img))
hog_descriptors = np.squeeze(hog_descriptors)
print('将数据集分成两份,90%用于训练,10%用于测试... ')
train_n = int(0.9 * len(hog_descriptors))
digits_train, digits_test = np.split(digits_deskewed, [train_n])
hog_descriptors_train, hog_descriptors_test = np.split(hog_descriptors, [train_n])
labels_train, labels_test = np.split(labels, [train_n])
print('训练SVM模型 ...')
model = svmInit()
svmTrain(model, hog_descriptors_train, labels_train)
print('Evaluating model ... ')
vis = svmEvaluate(model, digits_test, hog_descriptors_test, labels_test)
cv2.imwrite("digits-classification.jpg", vis)
cv2.imshow("Vis", vis)
cv2.waitKey(0)
cv2.destroyAllWindows()
'''
加载本地图片 ...
打乱数据 ...
纠偏 ...
定义HOG参数 ...
提取每张图片的HOG特征向量 ...
将数据集分成两份,90%用于训练,10%用于测试...
训练SVM模型 ...
Evaluating model ...
预测准确率: 99.00 %
confusion matrix:
[[52 0 0 0 0 0 0 0 0 0]
[ 0 43 2 0 0 0 0 0 0 0]
[ 0 0 61 0 0 0 0 1 0 0]
[ 0 0 0 49 0 0 0 0 0 0]
[ 0 0 0 0 44 0 0 0 0 0]
[ 0 0 0 0 0 49 0 0 0 0]
[ 0 0 0 0 0 0 46 0 0 0]
[ 0 0 0 0 0 0 0 50 1 0]
[ 0 0 0 0 0 1 0 0 50 0]
[ 0 0 0 0 0 0 0 0 0 51]]
500
'''
输出图片:
见 https://www.yuque.com/shuiguohaohaochio/cegzao/zz1has756r75kylg 。
最后此篇关于【opencv】传统图像识别:hog+svm实现图像识别详解的文章就讲到这里了,如果你想了解更多关于【opencv】传统图像识别:hog+svm实现图像识别详解的内容请搜索CFSDN的文章或继续浏览相关文章,希望大家以后支持我的博客! 。
背景: 我最近一直在使用 JPA,我为相当大的关系数据库项目生成持久层的轻松程度给我留下了深刻的印象。 我们公司使用大量非 SQL 数据库,特别是面向列的数据库。我对可能对这些数据库使用 JPA 有一
我已经在我的 maven pom 中添加了这些构建配置,因为我希望将 Apache Solr 依赖项与 Jar 捆绑在一起。否则我得到了 SolarServerException: ClassNotF
interface ITurtle { void Fight(); void EatPizza(); } interface ILeonardo : ITurtle {
我希望可用于 Java 的对象/关系映射 (ORM) 工具之一能够满足这些要求: 使用 JPA 或 native SQL 查询获取大量行并将其作为实体对象返回。 允许在行(实体)中进行迭代,并在对当前
好像没有,因为我有实现From for 的代码, 我可以转换 A到 B与 .into() , 但同样的事情不适用于 Vec .into()一个Vec . 要么我搞砸了阻止实现派生的事情,要么这不应该发
在 C# 中,如果 A 实现 IX 并且 B 继承自 A ,是否必然遵循 B 实现 IX?如果是,是因为 LSP 吗?之间有什么区别吗: 1. Interface IX; Class A : IX;
就目前而言,这个问题不适合我们的问答形式。我们希望答案得到事实、引用资料或专业知识的支持,但这个问题可能会引发辩论、争论、投票或扩展讨论。如果您觉得这个问题可以改进并可能重新打开,visit the
我正在阅读标准haskell库的(^)的实现代码: (^) :: (Num a, Integral b) => a -> b -> a x0 ^ y0 | y0 a -> b ->a expo x0
我将把国际象棋游戏表示为 C++ 结构。我认为,最好的选择是树结构(因为在每个深度我们都有几个可能的移动)。 这是一个好的方法吗? struct TreeElement{ SomeMoveType
我正在为用户名数据库实现字符串匹配算法。我的方法采用现有的用户名数据库和用户想要的新用户名,然后检查用户名是否已被占用。如果采用该方法,则该方法应该返回带有数据库中未采用的数字的用户名。 例子: “贾
我正在尝试实现 Breadth-first search algorithm , 为了找到两个顶点之间的最短距离。我开发了一个 Queue 对象来保存和检索对象,并且我有一个二维数组来保存两个给定顶点
我目前正在 ika 中开发我的 Python 游戏,它使用 python 2.5 我决定为 AI 使用 A* 寻路。然而,我发现它对我的需要来说太慢了(3-4 个敌人可能会落后于游戏,但我想供应 4-
我正在寻找 Kademlia 的开源实现C/C++ 中的分布式哈希表。它必须是轻量级和跨平台的(win/linux/mac)。 它必须能够将信息发布到 DHT 并检索它。 最佳答案 OpenDHT是
我在一本书中读到这一行:-“当我们要求 C++ 实现运行程序时,它会通过调用此函数来实现。” 而且我想知道“C++ 实现”是什么意思或具体是什么。帮忙!? 最佳答案 “C++ 实现”是指编译器加上链接
我正在尝试使用分支定界的 C++ 实现这个背包问题。此网站上有一个 Java 版本:Implementing branch and bound for knapsack 我试图让我的 C++ 版本打印
在很多情况下,我需要在 C# 中访问合适的哈希算法,从重写 GetHashCode 到对数据执行快速比较/查找。 我发现 FNV 哈希是一种非常简单/好/快速的哈希算法。但是,我从未见过 C# 实现的
目录 LRU缓存替换策略 核心思想 不适用场景 算法基本实现 算法优化
1. 绪论 在前面文章中提到 空间直角坐标系相互转换 ,测绘坐标转换时,一般涉及到的情况是:两个直角坐标系的小角度转换。这个就是我们经常在测绘数据处理中,WGS-84坐标系、54北京坐标系
在软件开发过程中,有时候我们需要定时地检查数据库中的数据,并在发现新增数据时触发一个动作。为了实现这个需求,我们在 .Net 7 下进行一次简单的演示. PeriodicTimer .
二分查找 二分查找算法,说白了就是在有序的数组里面给予一个存在数组里面的值key,然后将其先和数组中间的比较,如果key大于中间值,进行下一次mid后面的比较,直到找到相等的,就可以得到它的位置。

我是一名优秀的程序员,十分优秀!