Note：[ wechat：Y466551 | 可加勿骚扰，付费咨询 ]

论文信息

论文标题：Moka‑ADA: adversarial domain adaptation  with model‑oriented knowledge adaptation  for cross‑domain sentiment analysis 论文作者：Maoyuan ZhangXiang LiFei Wu 论文来源：2023 aRxiv 论文地址： download   论文代码：download 视屏讲解：click 。

1 介绍 

出发点 ：以往方法将特征表示转换为域不变的方法倾向于只对齐边缘分布，并且不可避免地会扭曲包含判别知识的原始特征表示，从而使条件分布不一致； 。

　　以往方法和本文方法的对比：我们采用对抗性判别域自适应（ADDA）框架来学习边际分布对齐的领域不变知识，在此基础上，在源模型和目标模型之间进行知识自适应以实现条件分布对齐。具体地说，我们设计了一个对中间特征表示和fnal分类概率具有相似性约束的对偶结构，以便训练中的目标模型从训练后的源模型中学习鉴别知识。在一个公开的情绪分析数据集上的实验结果表明，我们的方法取得了新的最先进的性能.

跨域情绪分析相关工作的联系 :

• • 伪标记技术[3,4]，使用在源标记数据上训练的模型，为未标记的目标数据生成伪标签，然后以监督的方式训练目标域的模型；　　
  • 基于枢轴的方法[5,6]，旨在选择域不变的特征，并将它们作为跨域映射的基础；
  • 对抗性训练方法[7,8]，目的是通过在模型训练过程中添加对抗性代价来学习输入样本的域独立映射，从而使源域分布和目标域分布之间的距离最小化；

方法对比 :

贡献 :

• • 提出了一种新的方法，Moka-ADA，来学习领域不变知识和判别知识，以确保边缘分布和条件分布同时对齐；
  • 设计了一个包含具有相似性约束的对偶结构的面向模型的知识自适应模块，使训练中的目标模型能够从训练后的源模型中学习鉴别性知识；
  • 采用知识蒸馏来促进鉴别知识的转移，这有助于增加类间距离，从而减少类内距离，并提高对抗性领域自适应的稳定性；
  • 在亚马逊审查基准数据集上进行了广泛的实验，平均准确率为94.25%，将CDSA任务的最新性能提高了1.11%；

2 方法

2.1 Model‑oriented knowledge adaptation

　　为了使训练中的目标编码器从训练后的源编码器中学习鉴别性知识，设计了一个面向模型的知识自适应模块，包括中间特征表示相似度约束（ISC）和最终分类概率相似度约束（FSC）.

2.1.1 Intermediate similarity constraints (ISC) based on the reproducing kernel hilbert space

　　源域数据 $\boldsymbol{x}_{s} \sim \mathbb{D}_{S}$，通过源域编码器 $E_{s}$ 和 目标编码器 $E_{t}$ 分别得到特征表示 $\boldsymbol{h}_{s}=E_{s}\left(\boldsymbol{x}_{s}\right)$、 $\hat{\boldsymbol{h}}_{t}=E_{t}\left(\boldsymbol{x}_{s}\right)$，且满足 $\boldsymbol{H}_{S}=\left\{\left(\boldsymbol{h}_{s}^{i}\right)\right\}_{i=1}^{n} \sim \mathbb{H}_{S}$  和 $\boldsymbol{H}_{T}=\left\{\left(\hat{\boldsymbol{h}}_{t}^{i}\right)\right\}_{i=1}^{n} \sim \mathbb{H}_{T} $，特征分布 $\mathbb{H}_{S}$ 和 $\mathbb{H}_{T}$ 之间的距离使用 $\text{MMD}$ 计算:

　　　　$\begin{aligned}\underset{E_{t}}{\text{min}} \; & \mathcal{L}_{\mathrm{ISC}}\left(\boldsymbol{x}_{s}\right) \\= & \operatorname{MMD}^{2}\left[\mathcal{F}, \boldsymbol{h}_{s}, \hat{\boldsymbol{h}}_{t}\right] \\= & \left\|\mathbb{E}_{\boldsymbol{h}_{s} \sim \mathbb{H}_{S}} \phi\left(\boldsymbol{h}_{s}\right)-\mathbb{E}_{\hat{\boldsymbol{h}}_{\boldsymbol{t}} \sim \mathbb{H}_{T}} \phi\left(\hat{\boldsymbol{h}}_{t}\right)\right\|_{\mathcal{H}}^{2} \\= & \mathbb{E}_{\boldsymbol{h}_{s}, \boldsymbol{h}_{s}^{\prime} \sim \mathbb{H}_{s}, \mathbb{H}_{S}} k\left(\boldsymbol{h}_{s}, \boldsymbol{h}_{s}^{\prime}\right) -  2 \mathbb{E}_{\boldsymbol{h}_{s}, \hat{\boldsymbol{h}}_{t} \sim \mathbb{H}_{s}, \mathbb{H}_{T}} k\left(\boldsymbol{h}_{s}, \hat{\boldsymbol{h}}_{t}\right)  +\mathbb{E}_{\hat{\boldsymbol{h}}_{t}, \hat{h}_{t}^{\prime} \sim \mathbb{H}_{T}, \mathbb{H}_{T}} k\left(\hat{\boldsymbol{h}}_{t}, \hat{\boldsymbol{h}}_{t}^{\prime}\right),\end{aligned}$ 。

　　其中，核函数 $k(\boldsymbol{u}, \boldsymbol{v})=\sum_{i=1}^{m} \exp \left\{-\frac{1}{2 \delta_{i}}\|\boldsymbol{u}-\boldsymbol{v}\|_{2}^{2}\right\}$； 。

2.1.2 Final similarity constraints (FSC) based on the knowledge distillation

　　传统的方法将对目标样本设置一个硬标签（伪标签），这在重复训练过程中容易造成过拟合。为了缓解这一问题，利用知识蒸馏（KD），通过产生一个软概率分布来控制知识转移的程度.

　　软概率分布的优势:

• • 软标签用多个概率值来描述概率分布，可以更好地处理噪声和不确定性；
  • 包含了不同类之间的相关性信息，有助于增加类间距离，从而减少类内距离；

　　接着将 $\boldsymbol{h}_{s}$、$\hat{\boldsymbol{h}}_{t}$ 放入放缩余弦分类器  。

　　　　$\boldsymbol{p}_{s}=C_{s}\left(\boldsymbol{h}_{s}\right)$　　$\hat{\boldsymbol{p}}_{t}=C_{s}\left(\hat{\boldsymbol{h}}_{t}\right)$　　$\boldsymbol{P}=\sigma\left(\boldsymbol{p}_{s} / T\right)$　　$\boldsymbol{Q}=\sigma\left(\hat{\boldsymbol{p}}_{t} / T\right)$ 。

　　最终相似性约束如下:

　　　　$\begin{aligned}\underset{E_{t}}{\text{min}} \; & \mathcal{L}_{\mathrm{FSC}}\left(\boldsymbol{x}_{s}\right) \\& =T^{2} \cdot \operatorname{KL}(\boldsymbol{P} \| \boldsymbol{Q}) \\& =T^{2} \cdot \mathbb{E}_{\boldsymbol{x}_{s} \sim \mathbb{D}_{S}} \sum_{k=1}^{K} P_{k} \log \frac{P_{k}}{Q_{k}},\end{aligned}$ 。

　　2.1 节小结：综上所述，对源编码器和目标编码器的输入是相同的，目标编码器用“中间”和“fnal”来模拟源编码器，从而实现条件分布对齐的鉴别知识.

笔记 :

　　传统的余弦相似度计算公式为:

　　　　cosine similarity = dot product(A, B) / (norm(A) * norm(B)) 。

　　其中，dot product(A, B)表示向量 A 和 B 的点积，norm(A) 和 norm(B) 分别表示向量 A 和 B 的范数.

　　放缩余弦分类器通过引入放缩因子来调整余弦相似度的计算，公式如下:

　　　　scaled cosine similarity = dot product(A, B) / (scale_factor * norm(A) * norm(B)) 。

2.2 Adversarial domain adaptation with model‑oriented knowledge adaptation

　　本文提出的 Moka-ADA 框架 如 Figure2 所示:

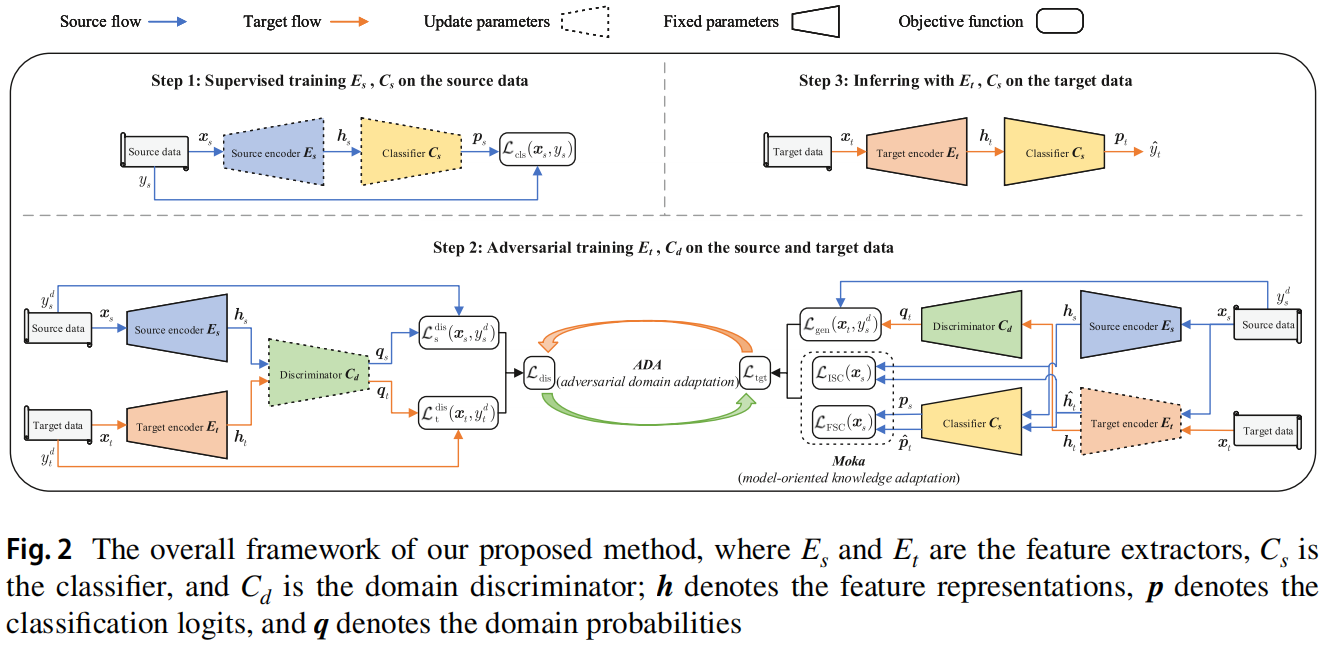
　　主要包括三个步骤:

• • Step1：对源数据上的源编码器 $E_s$ 和分类器 $C_s$ 进行监督训练；
  • Step2：对抗性训练目标编码器 $E_t$ 和鉴别器 $C_d$，以对齐源域和目标域分布；
  • Step3：利用训练后的目标编码器 $E_t$ 和分类器 $C_s$ 对目标数据进行推断；

Step1 ，目标是使用来自源域的标记数据来训练一个性能良好的源模型，它作为目标模型的后续训练的 “teacher”，通过使用交叉熵损失，通过对源编码器 $E_s$ 和分类器 $C_s$ 在 $(x_s,y_s)$ 进行监督训练，可以最小化源误差:

　　　　$\begin{array}{l}\underset{E_{s}, C_{s}}{\text{min}} \; \mathcal{L}_{\mathrm{cls}}\left(\boldsymbol{x}_{s}, y_{s}\right)=\mathbb{E}_{\left(\boldsymbol{x}_{s}, y_{s}\right) \sim \mathbb{D}_{S}}-\sum_{k=1}^{K} \mathbb{1}_{\left[k=y_{s}\right]} \log \sigma\left(\boldsymbol{p}_{s}\right)\end{array}$ 。

Step2 ，固定 $E_s$ 的参数，并使用 $E_s$ 初始化 $E_t$ 的参数，接着进行对抗性训练:

　　域分类损失最小化:

　　　　$\begin{aligned}\underset{C_{d}}{\text{min}} \; & \mathcal{L}_{\mathrm{dis}}\left(\boldsymbol{x}_{s}, \boldsymbol{x}_{t}, y_{s}^{d}, y_{t}^{d}\right) \\& =\min _{C_{d}}\left[\frac{\mathcal{L}_{\mathrm{s}}^{\mathrm{dis}}\left(\boldsymbol{x}_{s}, y_{s}^{d}\right)+\mathcal{L}_{\mathrm{t}}^{\mathrm{dis}}\left(\boldsymbol{x}_{t}, y_{t}^{d}\right)}{2}\right] \\& =\frac{\mathbb{E}_{\boldsymbol{x}_{s} \sim \mathbb{D}_{S}}-\log \left(1-\boldsymbol{q}_{s}\right)+\mathbb{E}_{\boldsymbol{x}_{t} \sim \mathbb{D}_{T}}-\log \boldsymbol{q}_{t}}{2} .\end{aligned}$ 。

　　域分类损失最大化（迷惑域鉴别器）:

　　　　$\begin{aligned}\underset{E_{t}}{\text{min}} \;\; & \mathcal{L}_{\text {gen }}\left(\boldsymbol{x}_{t}, {\color{Red} y_{s}^{d}} \right) \\\quad & =\mathbb{E}_{\boldsymbol{x}_{t} \sim \mathbb{D}_{T}}-\left[y_{s}^{d} \log \boldsymbol{q}_{t}+\left(1-y_{s}^{d}\right) \log \left(1-\boldsymbol{q}_{t}\right)\right] \\& =\mathbb{E}_{\boldsymbol{x}_{t} \sim \mathbb{D}_{T}}-\log \left(1-\boldsymbol{q}_{t}\right),\end{aligned}$ 。

　　注意：对抗性训练中的 特征提取器这边指的是 目标编码器 $E_t$； 。

　　目标编码器的最终训练目标:

　　　　$\begin{array}{l}\underset{E_{t}}{\text{min}}\;\mathcal{L}_{\mathrm{tgt}}\left(\boldsymbol{x}_{s}, \boldsymbol{x}_{t}, y_{s}^{d}\right) \\\quad= \underset{E_{t}}{\text{min}}\left[\mathcal{L}_{\mathrm{gen}}\left(\boldsymbol{x}_{t}, y_{s}^{d}\right)+\mathcal{L}_{\mathrm{ISC}}\left(\boldsymbol{x}_{s}\right)+\mathcal{L}_{\mathrm{FSC}}\left(\boldsymbol{x}_{s}\right)\right]\end{array}$ 。

Step3 ，使用训练好的目标编码器 $E_t$ 和分类器 $C_s$ 对用于测试的目标数据情绪极性标签预测如下:

　　　　$\hat{y}_{t}=\arg \max \boldsymbol{p}_{t}$ 。

2.3 算法流程

　　长这样的算法步骤:

3 实验

情绪分类结果 。

可视化 。

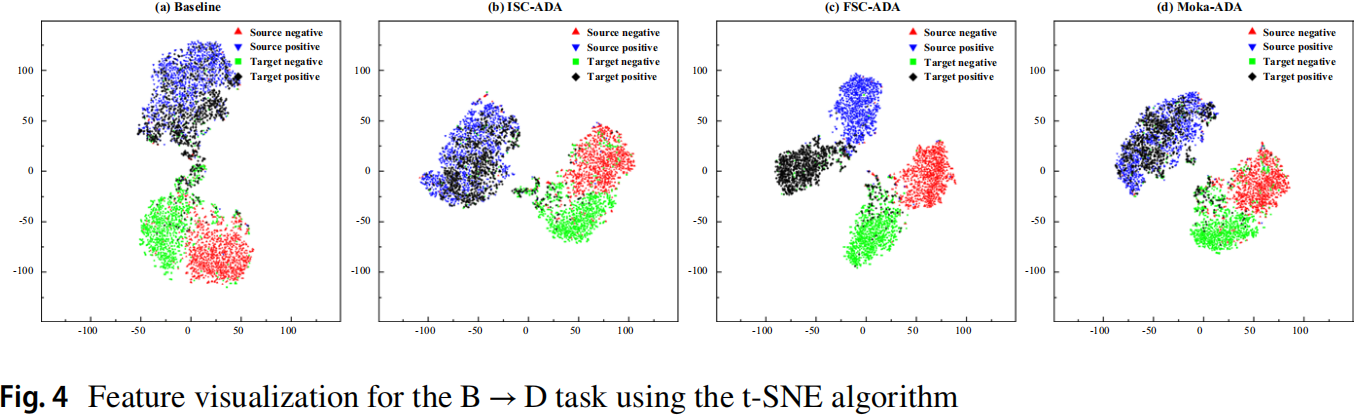
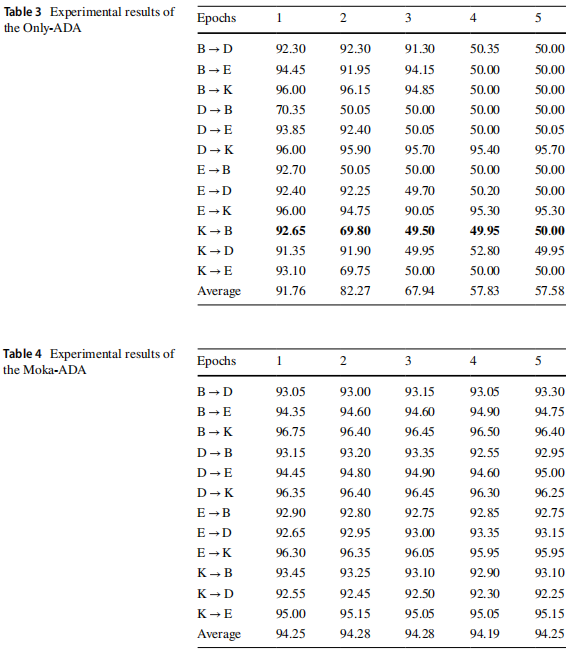
消融实验 。

最后此篇关于论文解读（Moka‑ADA）《Moka‑ADA:adversarialdomainadaptationwith model‑orientedknowledgeadaptationfor cross‑domainsentimentanalysis》的文章就讲到这里了,如果你想了解更多关于论文解读（Moka‑ADA）《Moka‑ADA:adversarialdomainadaptationwith model‑orientedknowledgeadaptationfor cross‑domainsentimentanalysis》的内容请搜索CFSDN的文章或继续浏览相关文章，希望大家以后支持我的博客！ 。