- Java锁的逻辑(结合对象头和ObjectMonitor)
- 还在用饼状图?来瞧瞧这些炫酷的百分比可视化新图形(附代码实现)⛵
- 自动注册实体类到EntityFrameworkCore上下文,并适配ABP及ABPVNext
- 基于Sklearn机器学习代码实战
[
20
,
40
,
60
]
/ |
\
[
5
,
10
] [
25
,
30
] [
45
,
50
,
55
,
58
]
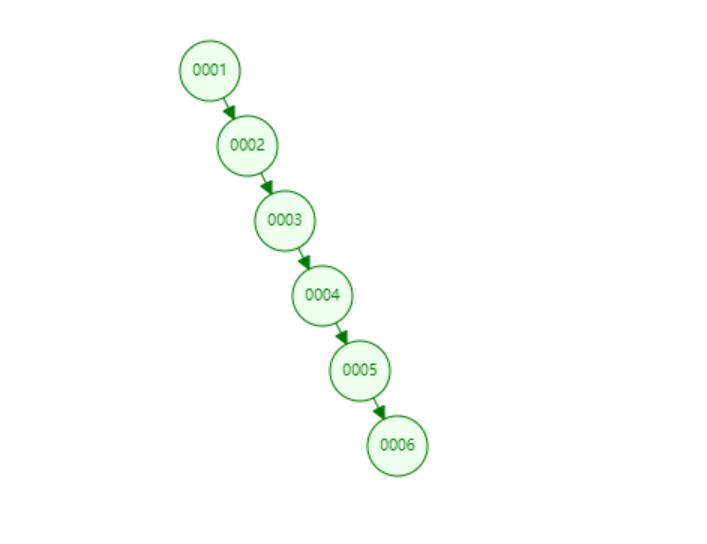
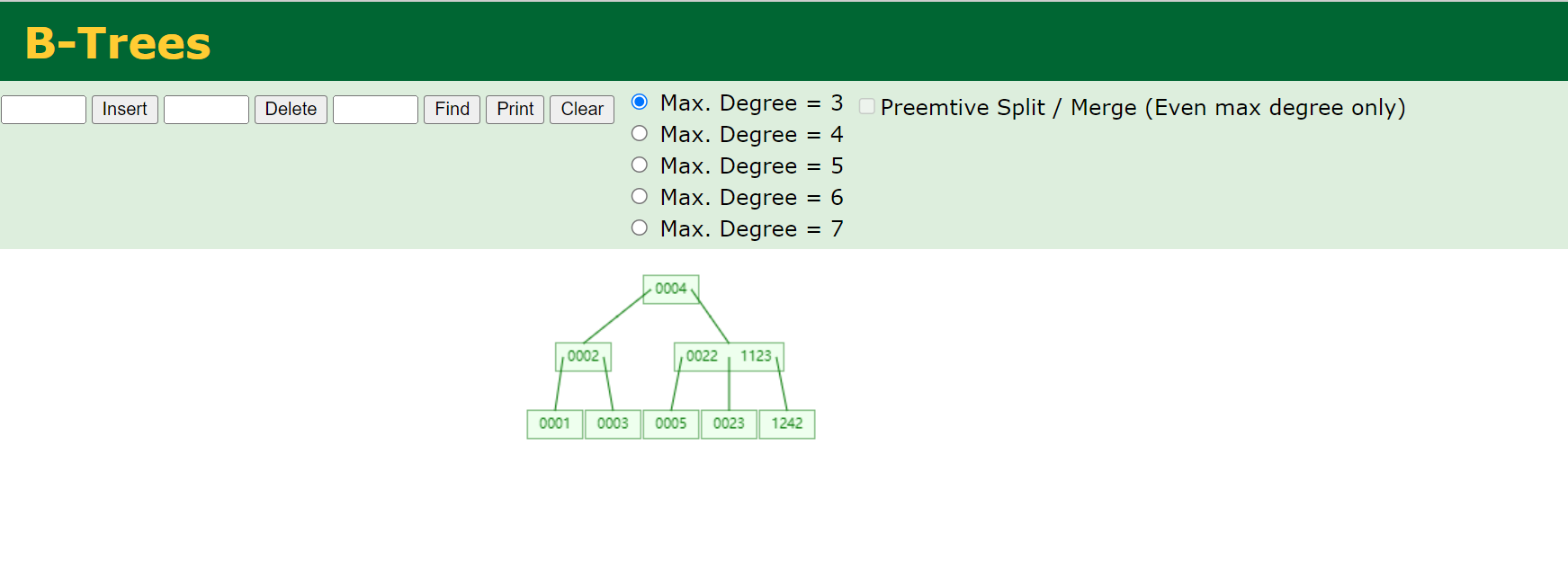
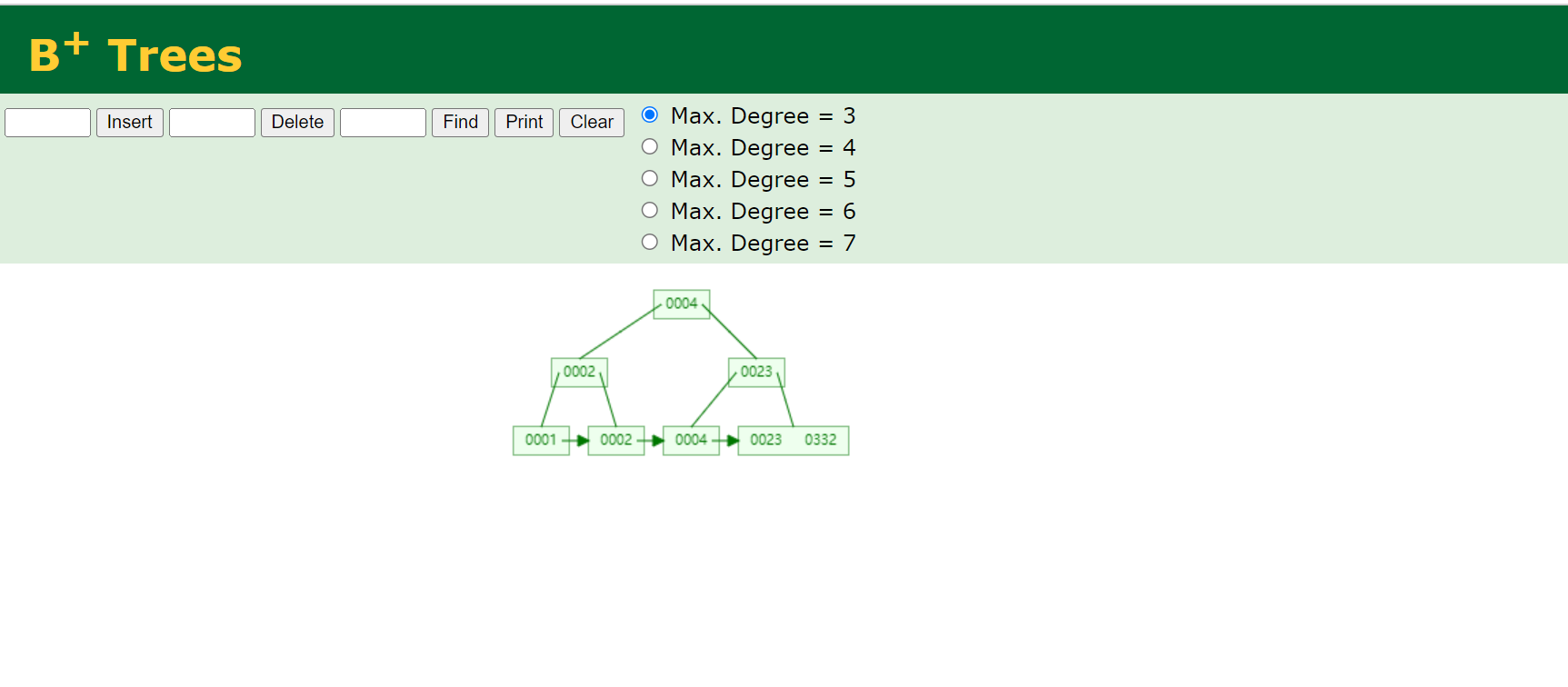
假设我们有一个B树的节点最大容量为3的情况。
在这个B树中,每个节点存储的键值数量不定,但都在一个范围内。每个非叶子节点既存储索引键值,又存储实际数据。
例如,节点[
20
,
40
,
60
]包含键值20、40和60,并且包含对应的子节点的指针。这样的设计使得B树在查找特定键值时,不仅可以找到索引位置,还可以直接获取数据。
[
40
]
/ |
\
[
5
,
10
,
20
]-> [
30
,
35
] ->[
45
,
50
,
55
,
58
]
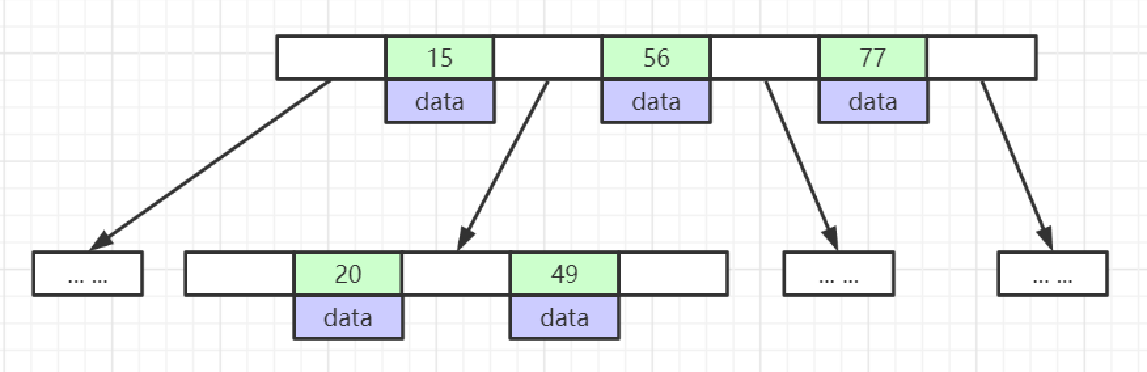
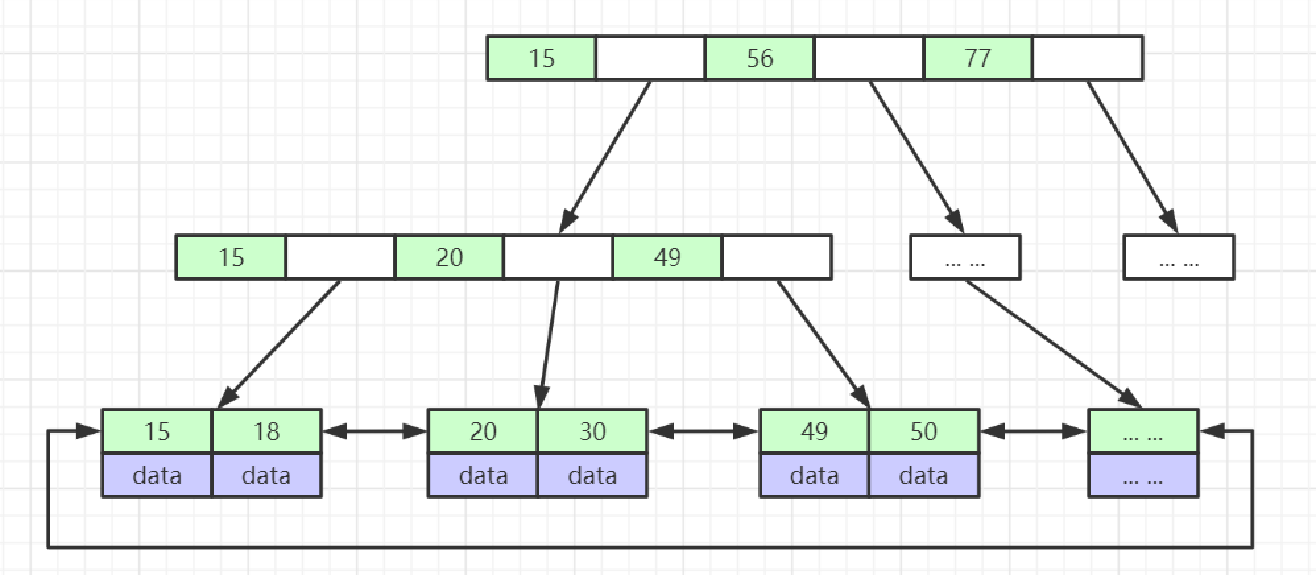
假设我们有一个B
+
树的节点最大容量为3的情况。
在这个B
+
树中,每个节点存储的索引键值数量更多,相比于B树,它具有更高的空间利用率。每个非叶子节点仅存储索引键值,而所有的数据项都存储在叶子节点中。
例如,节点[
40
]仅包含键值40,并且包含指向叶子节点的指针。这使得B+树的非叶子节点更加紧凑,只用于索引导航,不占用额外的空间来存储数据。
。
[
20
,
40
,
60
]
/ |
\
[
5
,
10
] [
25
,
30
] [
45
,
50
,
55
,
58
]
假设我们要进行键值在10到30之间的范围查询。范围查询需要在不同的层级之间跳转,增加了IO操作。
[
40
]
/ |
\
[
5
,
10
,
20
]-> [
30
,
35
] ->[
45
,
50
,
55
,
58
]
范围查询只需在叶子节点之间遍历有序链表,不需要在不同的层级之间跳转,减少了IO操作。

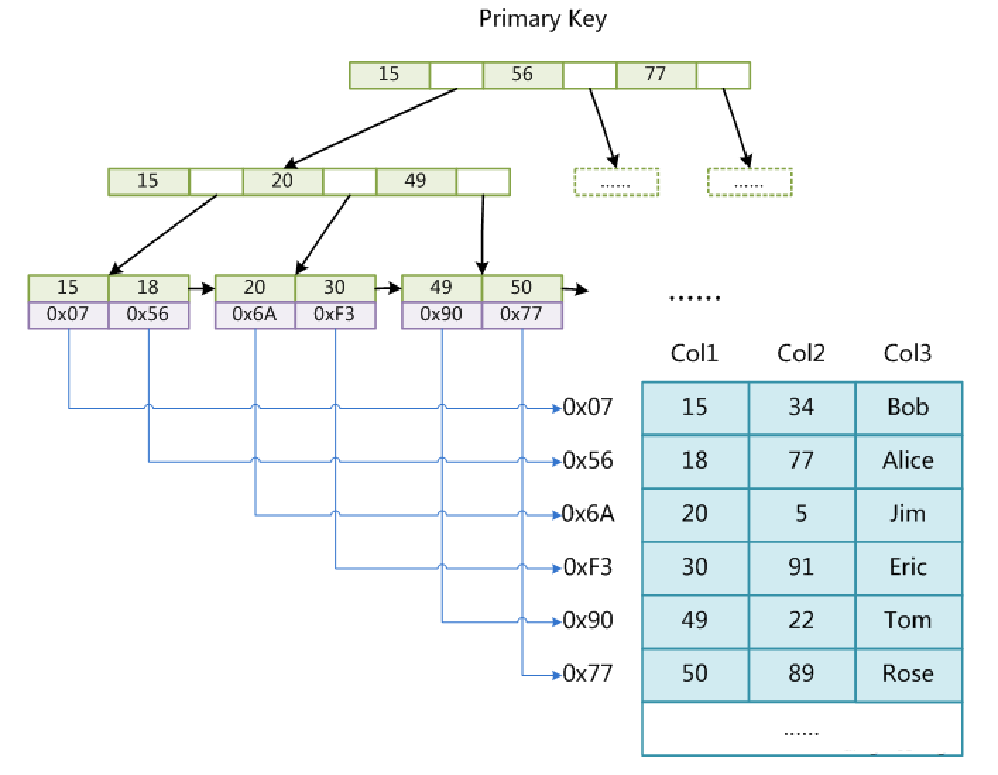
主键索引: [
1
: Alice] [
2
: Bob] [
3
: Charlie] [
4
: David] ...
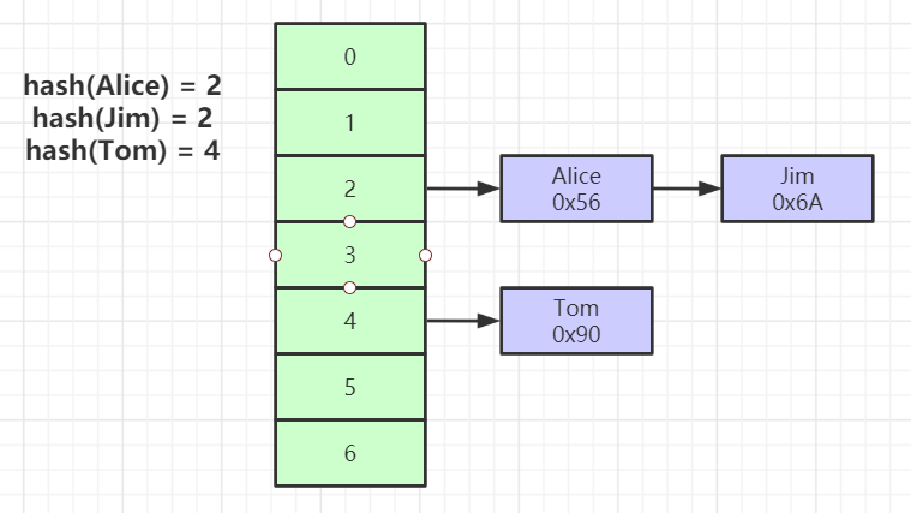
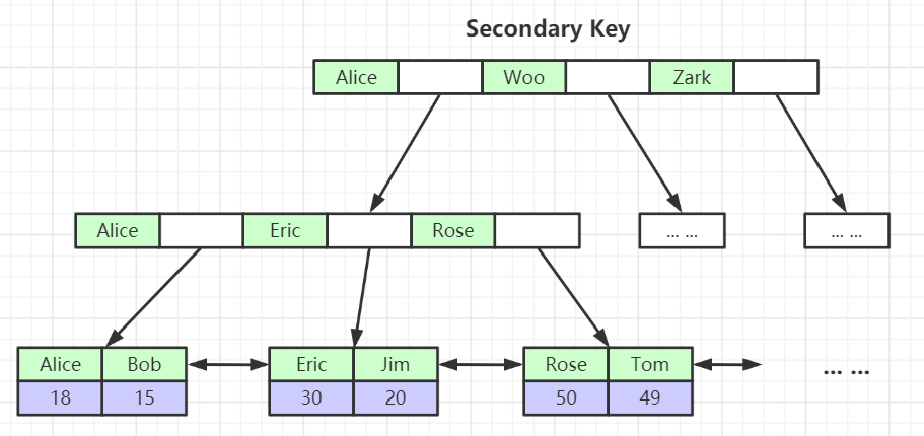
非主键索引: [Alice:
1
] [Bob:
2
] [Charlie:
3
] [David:
4
] ...
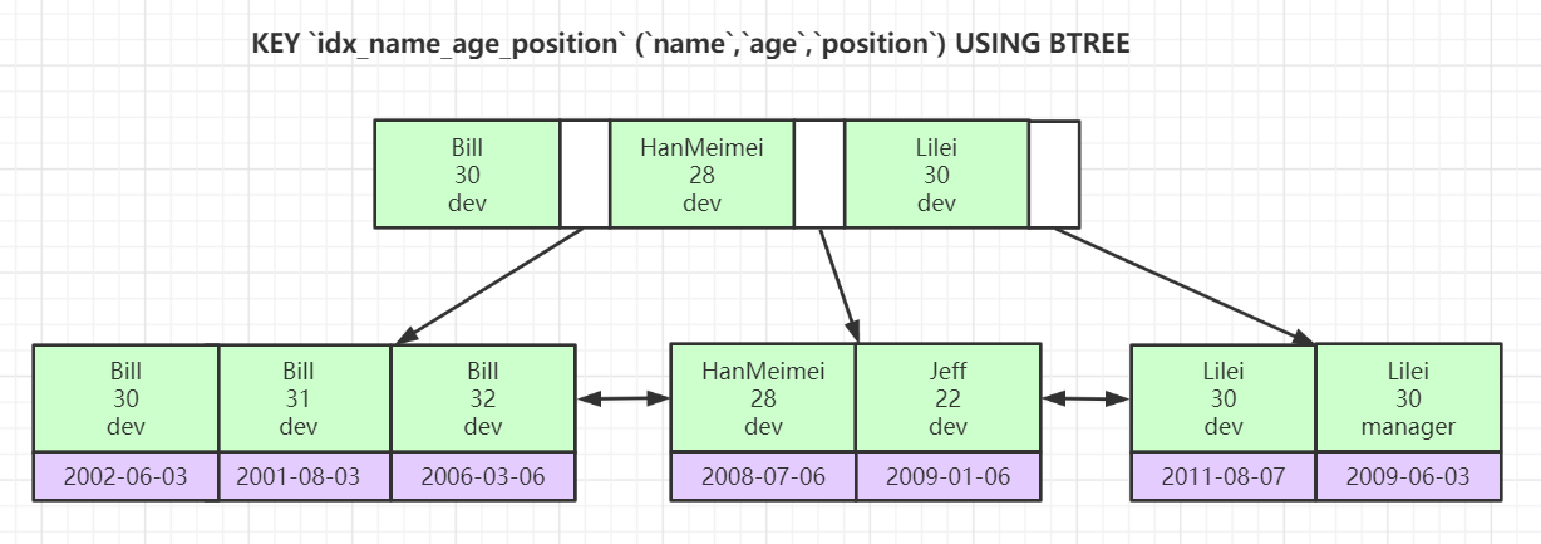
联合索引 (category, brand, price) 排序:
(Computers, Dell,
1000
)
(Computers, HP,
800
)
(Computers, Lenovo,
900
)
(Electronics, Samsung,
600
)
(Electronics, Sony,
700
)
(Furniture, Ikea,
300
)
(Furniture, Ashley,
400
)
(Furniture, Wayfair,
500
) ...
。
最后此篇关于深入理解Mysql索引的文章就讲到这里了,如果你想了解更多关于深入理解Mysql索引的内容请搜索CFSDN的文章或继续浏览相关文章,希望大家以后支持我的博客! 。
最近做一个项目,由于是在别人框架里开发app,导致了很多限制,其中一个就是不能直接引用webservice 。 我们都知道,调用webserivice 最简单的方法就是在 "引用"
这是SDL2代码的一部分 SDL主函数 int main(int argc,char *argv[]) { ... ... bool quit=false; S
c 中的函数: PHPAPI char *php_pcre_replace(char *regex, int regex_len, ch
我有以下映射: public class SecurityMap : ClassMap { public SecurityMap() {
我在vue-lic3中使用了SCSS,但是有一个奇怪的错误,使用/ deep /会报告错误,我不想看到它。 代码运行环境 vue-cli3 + vant + scss 的CSS /deep/ .van
我在深入阅读 C# 时遇到了这个我能理解的内容: 当它被限制为引用类型时,执行的比较类型完全取决于类型参数被限制为什么。 但是不能理解这个: 如果进一步限制派生自重载 == 和 != 运算符的特定类型
Closed. This question is opinion-based。它当前不接受答案。 想改善这个问题吗?更新问题,以便editing this post用事实和引用来回答。 3年前关闭。
有人可以详细介绍关于自赋值的运算符重载中的 *this 和 const 例如: Class& Class::operator=(const Class& other) { a = other.
在向树中插入新节点时,如何填充闭包表的深度/长度列? ancestor 和 descendant 中的值是来自另一个表的 ID,表示要以树结构排列的页面。 关闭表: ancestor desce
现在我正在阅读“深入了解 C#”。缺少的一件事是完成一章后我可以解决的一系列问题。那会帮助我理解我刚刚学到的概念。 哪里可以找到适合 C#3.0 的问题集? 谢谢 最佳答案 你可以试试LINQ 101
TypeScript 给 JavaScript 扩展了类型的语法,我们可以给变量加上类型,在编译期间会做类型检查,配合编辑器还能做更准确的智能提示。此外,TypeScript 还支持了高级类型用
是否有一个单行代码来获取生成器并生成该生成器中的所有元素?例如: def Yearly(year): yield YEARLY_HEADER for month in range(1, 13)
所以我阅读了一些与“什么是方法组”相关的 StackOverflow 问题以及其他互联网文章,它们在底线都说了同样的话——方法组是“一组重载方法” ". 但是,在阅读 Jon Skeet 的“C# 深
有什么方法可以从子组件中获取子组件吗? 想象一下以下组件树: 应用程序 问题 问题选项(包含复选框) 问题选项(包含复选框) 问题选项(包含复选框) 我想从 App 访问问题选项以选中所有复选框。 参
class_eval 和 instance_eval 在定义方法等情况下是完全可以预测的。我也理解类的实例和类的单例(又名特征类)之间的区别。 但是 我无法弄清楚以下唯一的事情:比方说,出于某些策略目
我想出了如何将符号 rwx 部分读取/转换为 421 个八进制部分,这非常简单。但是当涉及到特殊字符时,我感到非常困惑。我们知道 -r-xr---wx 转换为 0543,但 -r-sr---wt 或
我怀疑我系统的 Java 版本有问题。某些应用程序出现段错误或内存不足或存在链接错误。如果我从源代码安装了 JDK,我会做类似“make test”的事情,看看哪些测试失败了。但是,看起来从源代码构建
如何克隆一个 repo(使用 libgit2 ) 我想做什么git clone确实,但有 libgit2 .我可能要问的是什么 git clone确实很深入。 这是我目前正在做的: 初始化一个repo
00、头痛的JS闭包、词法作用域? 被JavaScript的闭包、上下文、嵌套函数、this搞得很头痛,这语言设计的,感觉比较混乱,先勉强理解总结一下😂😂😂.
我开始玩 lubridate R 中的包。我注意到 now(tzone="EST")计算为: [1] "2015-08-25 13:01:08 EST" 而 now(tzone="PST")导致警告:

我是一名优秀的程序员,十分优秀!