第四章 利萨茹曲线（Lissajous Curves）

原作：Keith Peters https://www.bit-101.com/blog/2022/11/coding-curves/ 。

译者：池中物王二狗(sheldon) 。

blog: http://cnblogs.com/willian/ 。

源码：github: https://github.com/willian12345/coding-curves 。

曲线艺术编程系列 第四章 。

确保您已知晓了最初一章中我们对示例代码的约定.

利萨茹曲线一直以来是我最喜欢的技术之一。除了循环的形状，实际上它可比看起来有用.

在这一篇中我们将覆盖它的基础知识，除此之外像往常一样，我们另外还得看看它在其它方面的应用.

基础

利萨茹曲线又名利萨茹图形或鲍迪奇曲线。两个名字都来自于 19 世纪研究和撰写它们的人名.

这些曲线图形由上下左右来回摆动循环的长曲线形成。在它们在纯粹的形状时（译者注：没有复杂多余线条时），让我们想起常常在老式科幻电影中显示在示波器上发光的图形.

公式

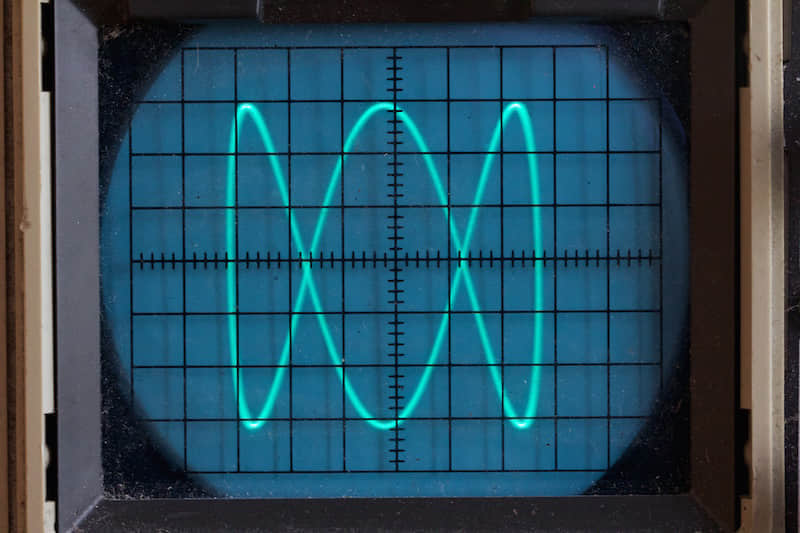
此番，在一开始我搜索利萨茹曲线相关题材时就找到了一个有用的参数方程.

                        
                          x = A * sin(a * t + d)
y = B * sin(b * t)

                        
                      

有一个正弦波在 x 轴，另一个正弦波在 y 轴。 它们不会在某个方向上趋向无限，它在周期内自循环.

公式中变量挺多的。让我们分别看看.

A 和 B 最后影响的是曲线在 x 轴宽和 y 轴高。确切的讲，只是宽高的一半，因为会在它各自方向上延展.

t 是一个范围 在 0 到 2 * PI 的范围参数变量。尽管在真正执行时它在各自方向上会超出范围，但很快它就会返回回来。在 x 方程式中 t 乘以 a, y 方程式中 t 乘以 b ，然后在各自轴结果传入正弦函数。另外，在 x 方程式中参数 d 或者说 delta 变量用于把它移出相位.

此方程可能看起来像之前章节中我们接触的圆方程。如果我们将 A 和 B 设为相等并且把它当作 r ，并且将 a 和 b 设为 1，再去掉 d ,再用余弦代替 x 方程的 正弦函数，我们就得到了:

                        
                          x = r * cos(t)
y = r * sin(t)

                        
                      

这就是原点在 0，0 的圆方程了。因为余弦就是正弦 +90 度，所以我们也可以说:

                        
                          x = r * sin(t + d)
y = r * sin(t)

                        
                      

... 这个 d 就是 90 度 ，或者 PI / 2 弧度.

A 和 B 分开的情况你在椭圆方程里已经见过了， 在那里 A 我们叫作 '半径 x', B 就是 “半径 y” 。

                        
                          x = A * sin(t + d)
y = B * sin(t)

                        
                      

所以当参数像上面那样同步变化，我们得到的是圆或椭圆，但当我们改动一些参数后，我们将得到了更有趣的曲线.

好了，说的够多了，开始编码吧。我们直接跳到创建一个利萨如函数。我会简化一下.

                        
                          function liss(cx, cy, A, B, a, b, d) {
  res = 0.01
  for (t = 0; t < 2 * PI; t += res) {
    x = cx + sin(a * t + d) * A
    y = cy + sin(b * t) * B
    lineTo(x, y)
  }
  closePath()
}

                        
                      

此处，分辨率变量 res 值不像之前在圆和椭圆函数内那样。在这里我给了一个很小的值，尽管它意味着画更多简单的小曲线。这样设定后从 0 到 2 * PI (6.28...), 从 0.01 开始增长将会得到 528 条线段，这对大多数例子来说足够用了（译者注：线段越多意味着越平滑）。如果曲线变的不平滑了，你就改这个值让线段变的更多。但我不打算深入测算到一个合适的值.

现在我们能用它画出来像下面这样调用:

                        
                          width = 600
height = 600
canvas(600, 600)
 
liss(300, 300, 250, 250, 1, 1, PI / 2)
stroke()

                        
                      

这个图就像我上面说的那样，我把 A 和 B 设为相等的值，a 和 b 设为 1 并且 d 设为 PI / 2 。这样实际得到的结果就是一个圆形... 。

... 看，确实是圆.

让我们先将 d 设为 0 然后 a 和 b 稍后小变化一下子。 这里，将 a 和 b 分别设置为 2 和 1（再次 d 设为 0） 。

                        
                          liss(300, 300, 250, 250, 2, 1, 0)


                        
                      

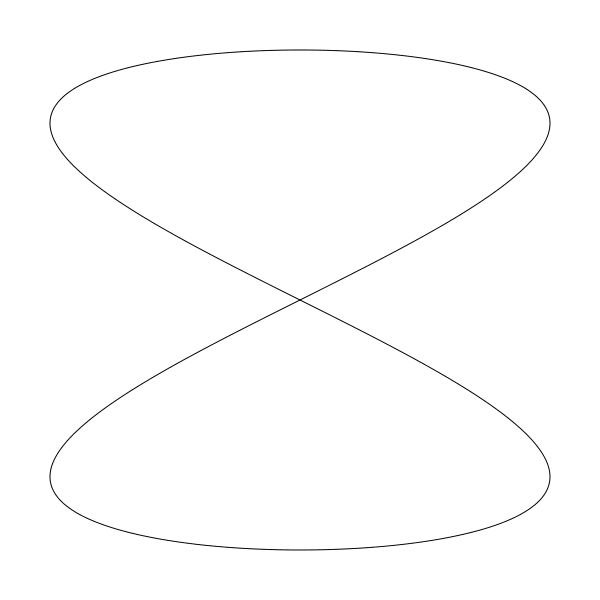
设为 2 和 3 时:

                        
                          liss(300, 300, 250, 250, 2, 3, 0)


                        
                      

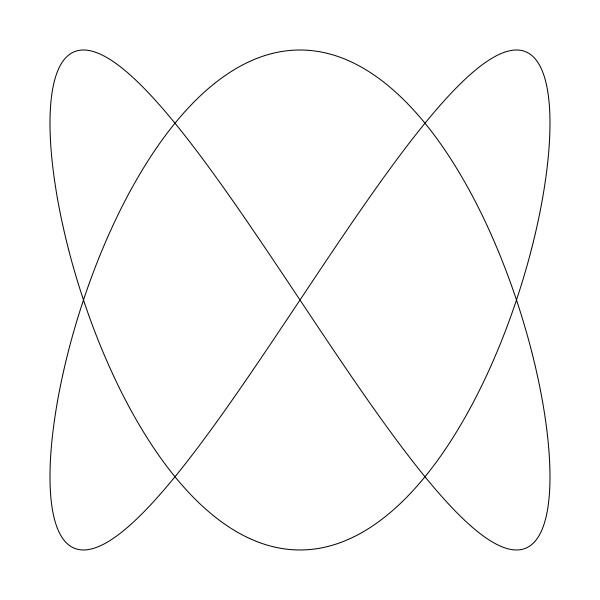
让我们调的更大一点，11 和 8 。

                        
                          liss(300, 300, 250, 250, 11, 8, 0)


                        
                      

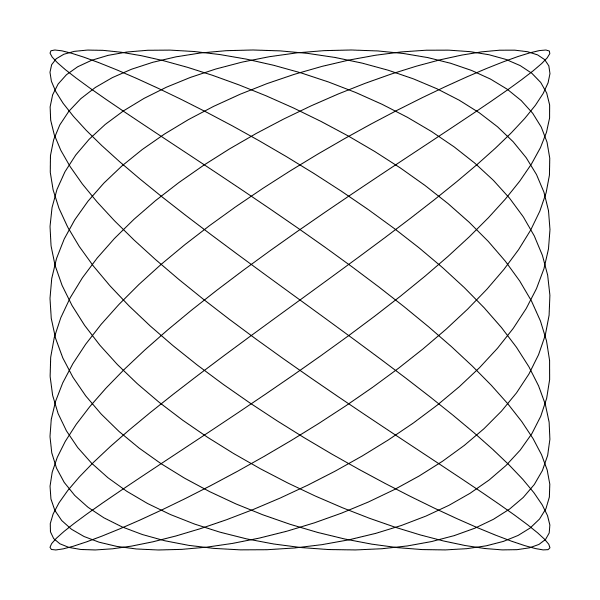
以上的这几个例子都中 d 都是 0， 波形都在自己轴的相位。现在我们保持 11 和 8 不变，将 d 变成 0.5， 移出它们的相位.

                        
                          liss(300, 300, 250, 250, 11, 8, 0.5)


                        
                      

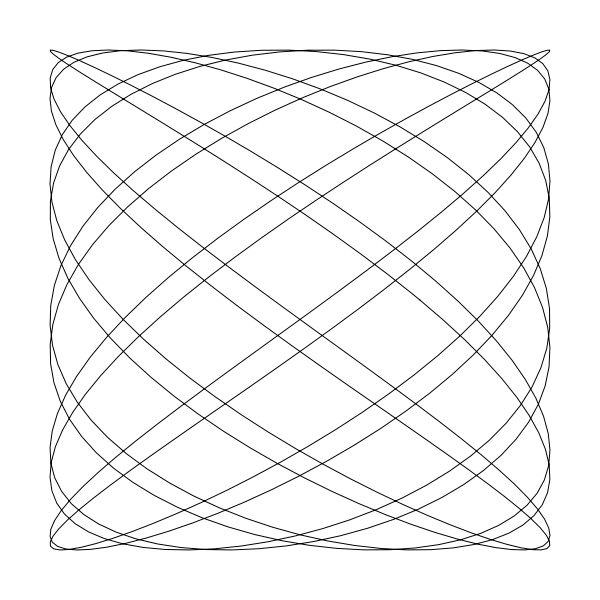
这里的动画是 a 为 6，b 为 7， d 持续变化时产生的图形变化 。

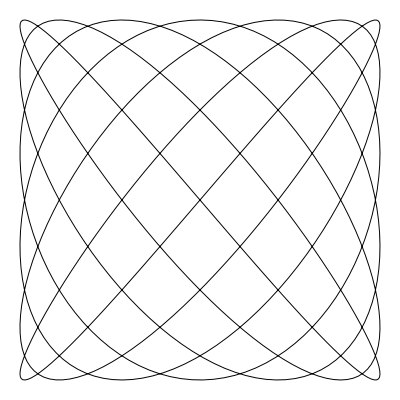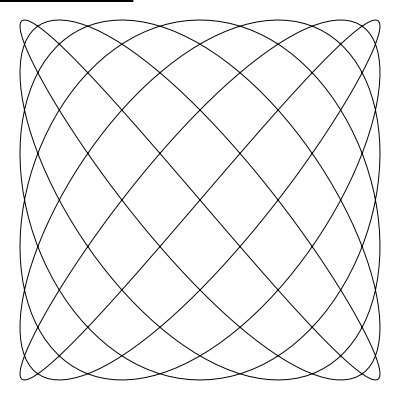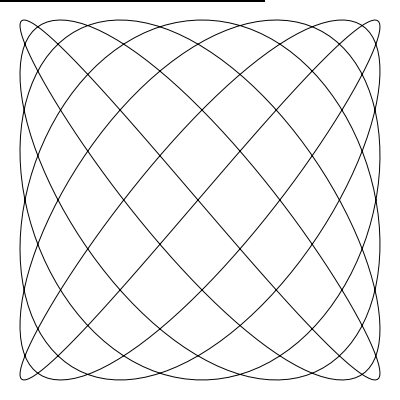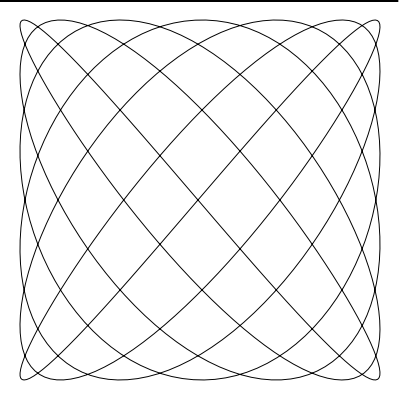
如果你希望你创建的曲线首尾丝滑的连接，那么没有什么 比 a 和 b 不是整数更糟的了（译者注：想丝滑需要 a 和 b 为整数）。 如果你将 a 设为 6.4，b 设为 7.3 。

                        
                          liss(300, 300, 250, 250, 6.4, 7.3, 0)

                        
                      

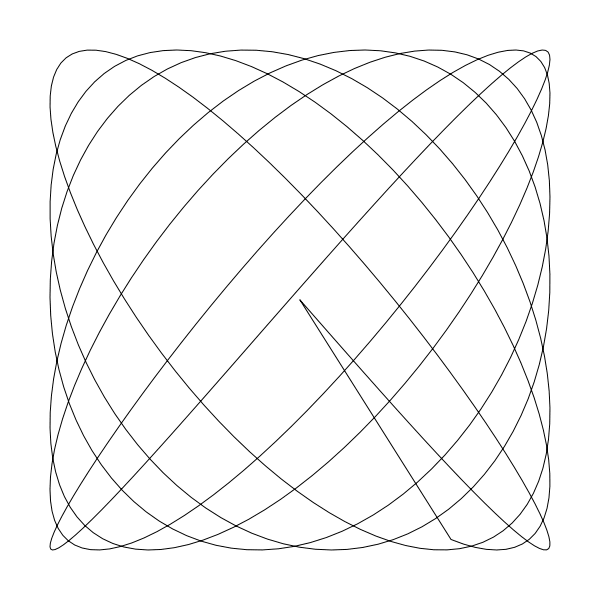
如果你想看清楚点发生了啥，那么将 closePath 从函数内注释掉看看结果:

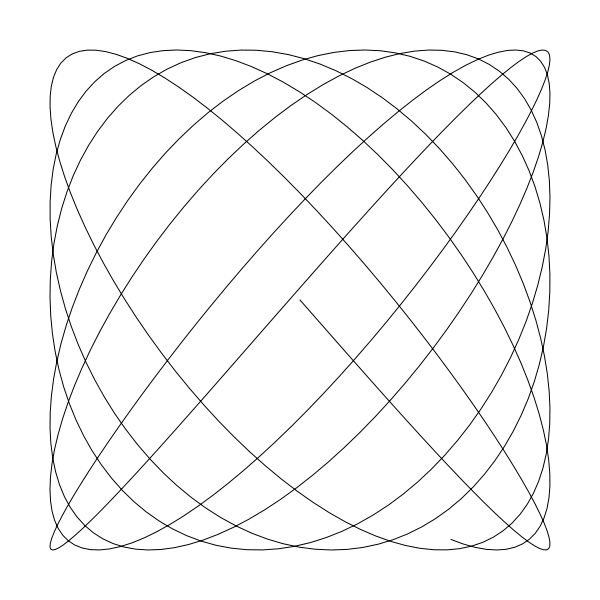
现在你可以看到曲线开始与结束点在随机位置， 而不是像 a 与 b 为整数时丝滑的连接起来.

当然，当你在这里使用小数时，你可以将变量 t 的范围从 0 到 2 * PI 继续放大到可以填满整个空间。 这里是我将 t 范围扩展到 20 * PI 的效果:

如果 a 和 b 你使用了有理数路径将最终又连接起来。 但可能会花点时间（译者注：如果是在动画中）。这个图中看起来就基本很接近了.

我们当然也能通过改变 A 和 B 这两个变量来获取宽的图形:

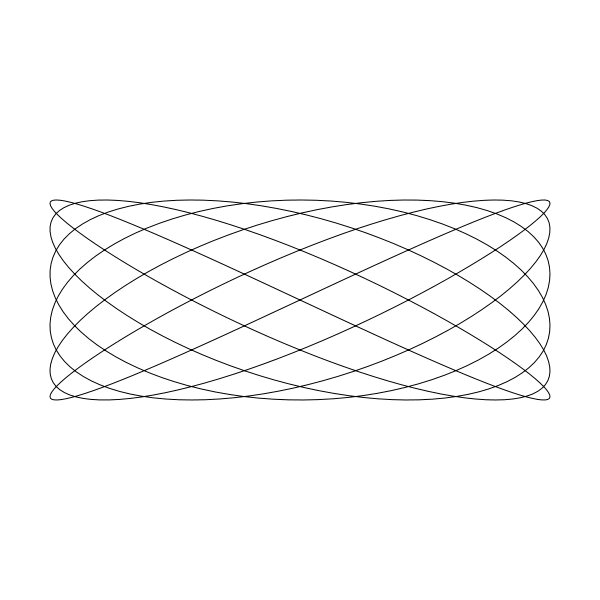
A = 250, B = 100 。

or tall figures

或高的 。

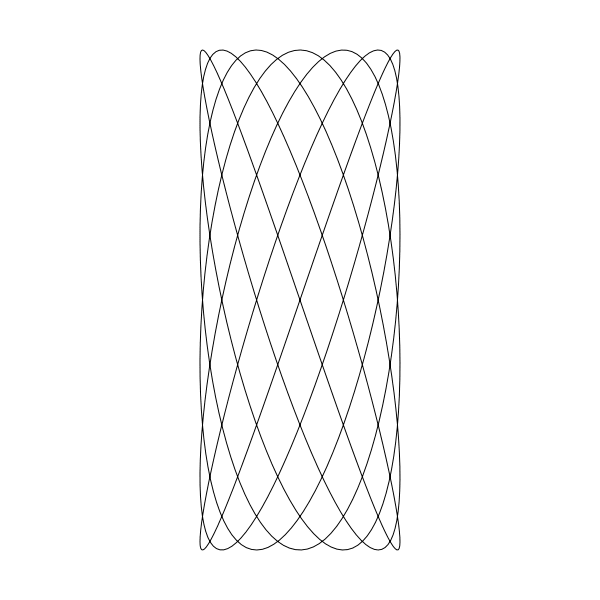
A = 100, B = 250 。

这就是绘制利萨茹图形最直接的方法。 可以查查维基百科与此相关的资料，学习一下这类曲线的多种属性。 我考虑在这里创建一个可交互的 demo， 但最后发现网上已经有很多了。文章最后我放了一些链接 。

取而代之的是，我们可以看看另外的应用方向.

动画

此处不会像上面做的曲线动画一样，不讨论曲线自身的动画，但会利用利萨茹曲线的结果应用在某个对象上.

但，首先我们先聊一聊最基础的动画 。

摆动(振荡)

通常你想在屏幕上对一个对象进行动画但又不想它超出屏幕， 让它上下左右的动，或者对它进行扭曲，变大，缩小。 你可能已经学习过一些 2D 图形变形属性，平移，旋转，缩放。 你可以用正弦或余弦函数计算结果值应用于这些变形属性，随着时间的推移改变那些函数方法的输入值就可以.

我们需要扩展一下我们的伪代码，它包含一个 loop 循环函数用于时刻进行不同绘制，它运行起来就是动画了。Processing （译者注：一个著名的图形库） 已经有内建的功能，其它图形系统也有类似的功能。但是你可能需要自己编写一个函数来实现这些功能。如果你用的是 HTML 和 javascript 的，那么我们可以使用 requestAnimationFrame 函数来实现.

我们假定它也拥有一个 clearCanvas 方法。我们可以把上一篇中编写的 circle 函数用到此处，或者使用你编码平台内置的绘图 api 。 我们像下面这样开始:

                        
                          width = 400
height = 400
t = 0
canvas(width, height)
 
function loop() {
  clearScreen()
  circle(width / 2 + sin(t) * 100, height / 2, 20)
  fill()
  t += 0.1
}

                        
                      

这里将正弦中的 t 乘以 100 以获得圆在 x 轴上的偏移。当 t 持续增长时，这个圆会来回运动。你也可以简单的对 y 轴应用同样的效果。或者应用在半径上:

                        
                          width = 400
height = 400
t = 0
canvas(width, height)
 
function loop() {
  clearScreen()
  circle(width / 2, height / 2, 50 + sin(t) * 20)
  fill()
  t += 0.1
}

                        
                      

此处，我们用 50 作为基础半径，加上使用 t 的正弦值乘以 20。由于 正弦值从 -1 到 +1 ，半径会加上 -20 到 +20 , 结果就是 30 至 70 之间摆动.

我们同样也可以将此应用在旋转属性上，但需要换一下图形，以便于我们可以观察到它的旋转。我把这个留给你自己实现吧.

回到绕圆运动。我们希望它绕整个 canvas 做圆周运行。我们一样可以使用正弦配合余弦完成圆周运动:

                        
                          width = 400
height = 400
t = 0
canvas(width, height)
 
function loop() {
  clearScreen()
  circle(width / 2 + cos(t) * 100, height / 2 + sin(t) * 100, 20)
  fill()
  t += 0.1
}

                        
                      

假设我们希望它运动的更加自然该如何实现？我们可以为它添加一些随机运动，然后你会发现一个问题，如何保证它只在屏幕内运动。不难，我们可以使用利萨茹的公式来实现这一点，像下面这样:

                        
                          width = 400
height = 400
t = 0
a = 13
b = 11
canvas(width, height)
 
function loop() {
  clearScreen()
  circle(width / 2 + sin(a * t) * 100, height / 2 + sin(b * t) * 100, 20)
  fill()
  t += 0.02
}

                        
                      

虽然这是一个不太完美的循环运动 gif 动画，但精神你肯定已经领会到了。这个圆看起来就像是随机绕着屏幕运动，但它实际是按利萨茹曲线路径运动。在我看来它就像是一只苍蝇在来回飞。事实上如果你多添加一些应用不同的参数的圆，那么它们会看起来更像一群苍蝇在飞。没有公分母的 a 和 b 数值设的越高，它在路径的运动看起来会更加随机.

利萨茹网络和随机利萨茹网络

下面这些图并非“标准官方”的图形，你可以在任何地方找到相关文档（可能我以前在某个地方提到过），但我始终觉得相互交流不同的创意是非常好的。你常常可以创造出一些独一无二的东西。所以我就放一些我自创的图在这里吧.

一些年前我曾经使用过利萨如曲线并尝试在不同的方式渲染它们。不仅仅是渲染它自己的路径，我决定用曲线上的每个相近点连接成线条。结果非常酷炫， 我将它们称为“利萨茹网络”。这里是一些例子:

你可以在这里找到更多 http://www.artfromcode.com/?p=657 。

我觉得它们看起来超酷。这些技术包含在了 Generative Design 这本书中 （信我） 。

随着我创意持续的进步， 我希望让它们更加的自然。 而不是仅仅给 a 和 b 添加乘数，我开始让这些参数变的随机一点。这会生成真正惊艳的图，我把它们称作“随机利萨茹网络” 。

它成为了我最爱欢迎作品这一。几年后我甚至被委托用此项技术设计一个系列印在红酒瓶上.

（译者注：红酒网站打不开...） 。

我就不再亮代码了。希望更多是对你的启发 -- 如何利用利萨茹曲线这一概念让颠覆事物让它变的更有趣.

下一章我们将聚焦在一些相关的系统上，它们同样使用非常有趣的方式创建曲线.

本章 Javascript 源码 https://github.com/willian12345/coding-curves/blob/main/examples/ch04/ 。

---

博客园: http://cnblogs.com/willian/ github: https://github.com/willian12345/ 。

最后此篇关于曲线艺术编程codingcurves第四章利萨茹曲线（LissajousCurves）的文章就讲到这里了,如果你想了解更多关于曲线艺术编程codingcurves第四章利萨茹曲线（LissajousCurves）的内容请搜索CFSDN的文章或继续浏览相关文章，希望大家以后支持我的博客！ 。