【技术分享】万字长文图文并茂读懂高性能无锁 “B-Tree 改”：Bw-Tree

原文链接： https://mp.weixin.qq.com/s/I5TphQP__tHn6JoPcP--_w 参考文献不一定能下载。如果你获取不到这几篇论文，可以关注公众号 IT技术小密圈 回复 bw-tree 获取.

一. 背景

Bw-Tree 希望实现以下能力

• 解决多核处理器性能瓶颈
  • 通过 CAS 操作实现 latch-free 能力, 提高多核 CPU 利用率。
  • 通过增量更新提高 CPU 缓存命中率。
• 利用更为高效的闪存：虽然闪存有着相似的随机读速度和顺序读速度，但其随机写速度远小于顺序写操作。 Log-Structured Store(LSS), 可以很好的利用这一点实现高效读写。

二. 基于 Bw-Tree 的存储整体架构

映射表

缓存层中维护着 映射表(mapping table ), 保存逻辑页和物理页的映射关系，逻辑页由逻辑页标识符 PID 唯一标识.

映射表将 PID 映射为以下两种地址之一

• 闪存偏移量(flash offset) : 持久化存储中的页的地址；
• 内存指针(memory pointer) : 内存页的地址。

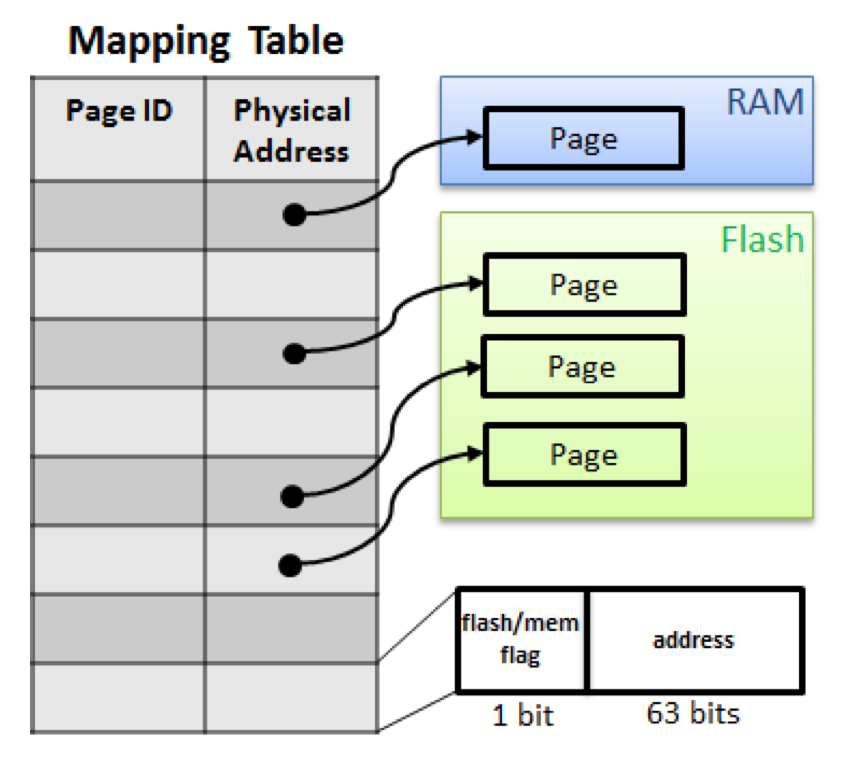
BW-Tree 的节点指针都是逻辑的 PID，因此在 SMO 操作过程中， 某些节点的物理地址发生变化，并不需要更新所有对该节点有引用的所有节点指针(PID 并没有发生变化).

增量更新

BW-Tree 通过创建描述变更内容的 增量记录(delta record) 并将其插入到当前页的前面来实现对页的状态变更.

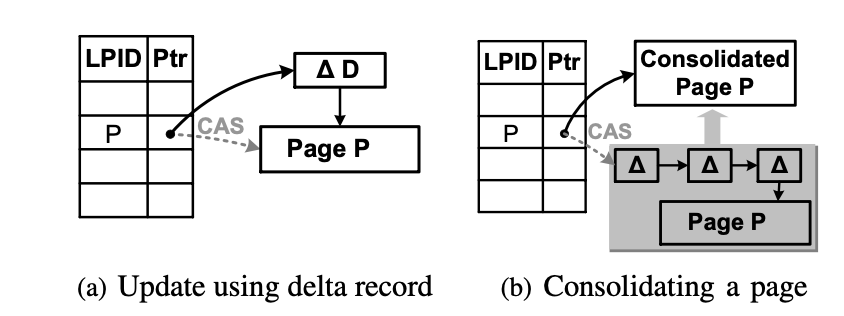
如下图 (a) 中，先将对 Page P 的一次变更操作做成一个增量记录 ∆D ，并让 ∆D 指向 Page P。然后将 Page P 的逻辑地址 PID P 映射的物理地址通过 CAS(compare and swap) 原子操作由 Page P 的物理地址改为 ∆D 的物理地址。(Page P 被称为 Base 页) 。

当变更导致前置的增量记录达到一定的规模之后，会触发合并操作，将所有的增量记录和原本的页合成一个新的页.

如下图(b) 中，将 Page P 前置的所有增量记录和 Page P 一起合并为一个 Consolidated Page P ， 然后通过 CAS 操作将 Page P 的逻辑地址 PID P 映射的物理地址替换为 Consolidated Page P 的物理地址。Page P 及其前置的所有增量记录将会被垃圾回收机制回收处理.

日志存储(Log Structure Store) 和 WAL(Write-Ahead Log) 日志

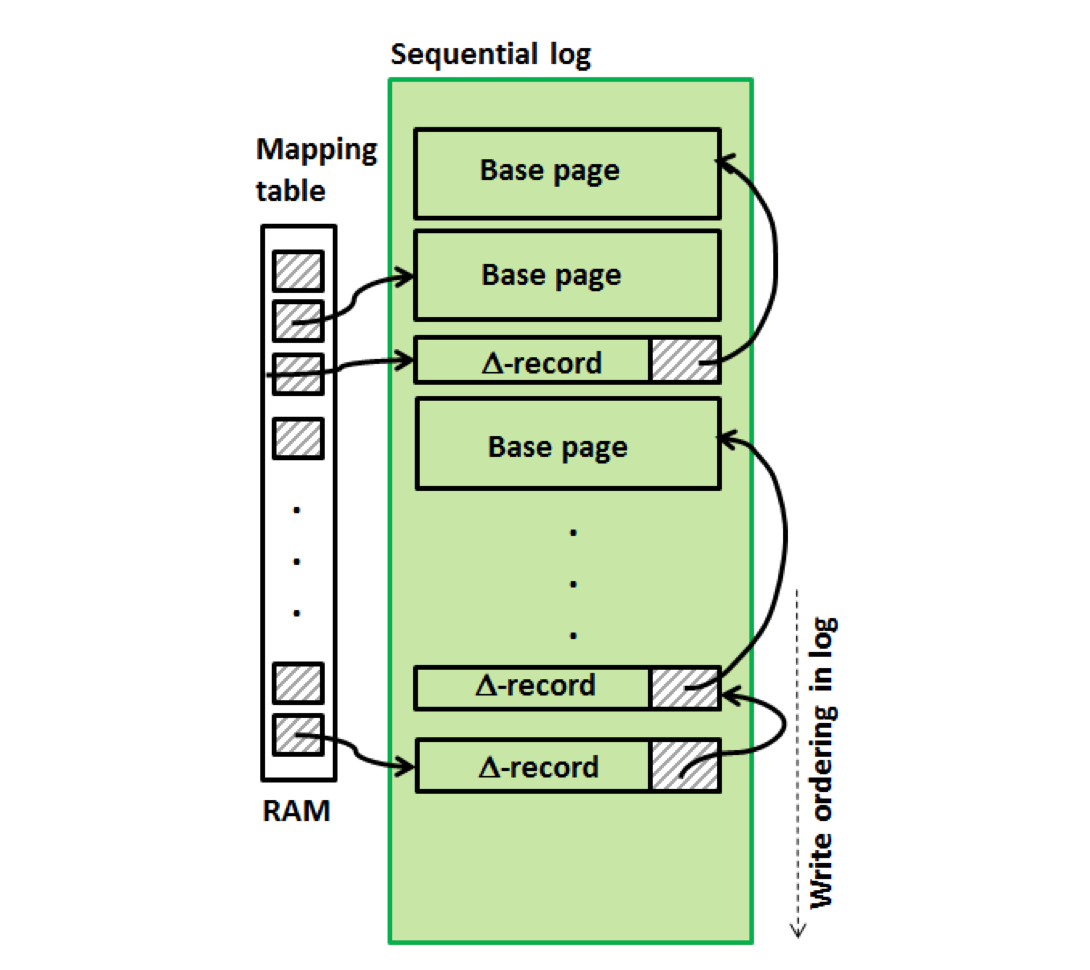
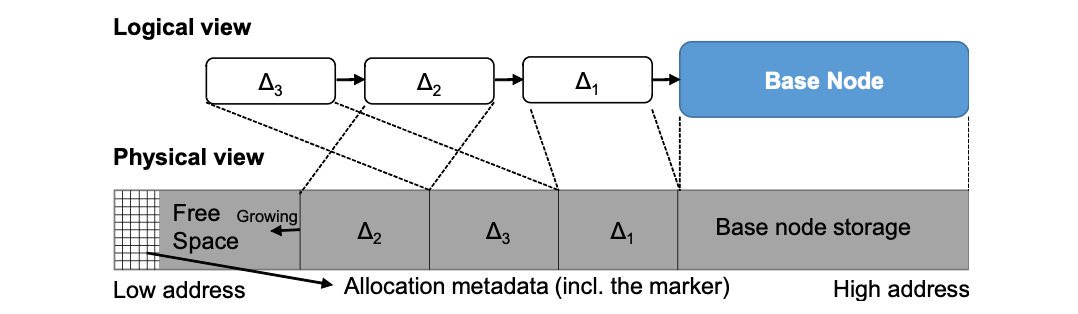
BW-Tree 在闪存中的存储结构如下图。当增量记录( ∆record )达到一定数量之后，会执行一次刷盘操作将所有 Base 页的增量记录一起顺序写入磁盘.

这将会导致每一个 Base 页和它对应的许多 ∆record 并不在相邻的地址内，而闪存的随机读性能和顺序读性能几乎一致，因此可以接受。(如果是其他顺序读性能更好的持久化存储可能需要一定优化，后文有提及。) 。

如上文所述， 并不是所有的变更操作都立即刷盘(而是会等待增量记录达到一定数量规模才会一次刷盘)。因此，在每次执行变更前，记录 WAL 日志也是必要的.

给每一次变更操作一个日志序列号(LSN), 当某次刷盘完成之后， 对应的最新 LSN 之前的 WAL 日志都可以失效.

BW-Tree 架构

整体架构

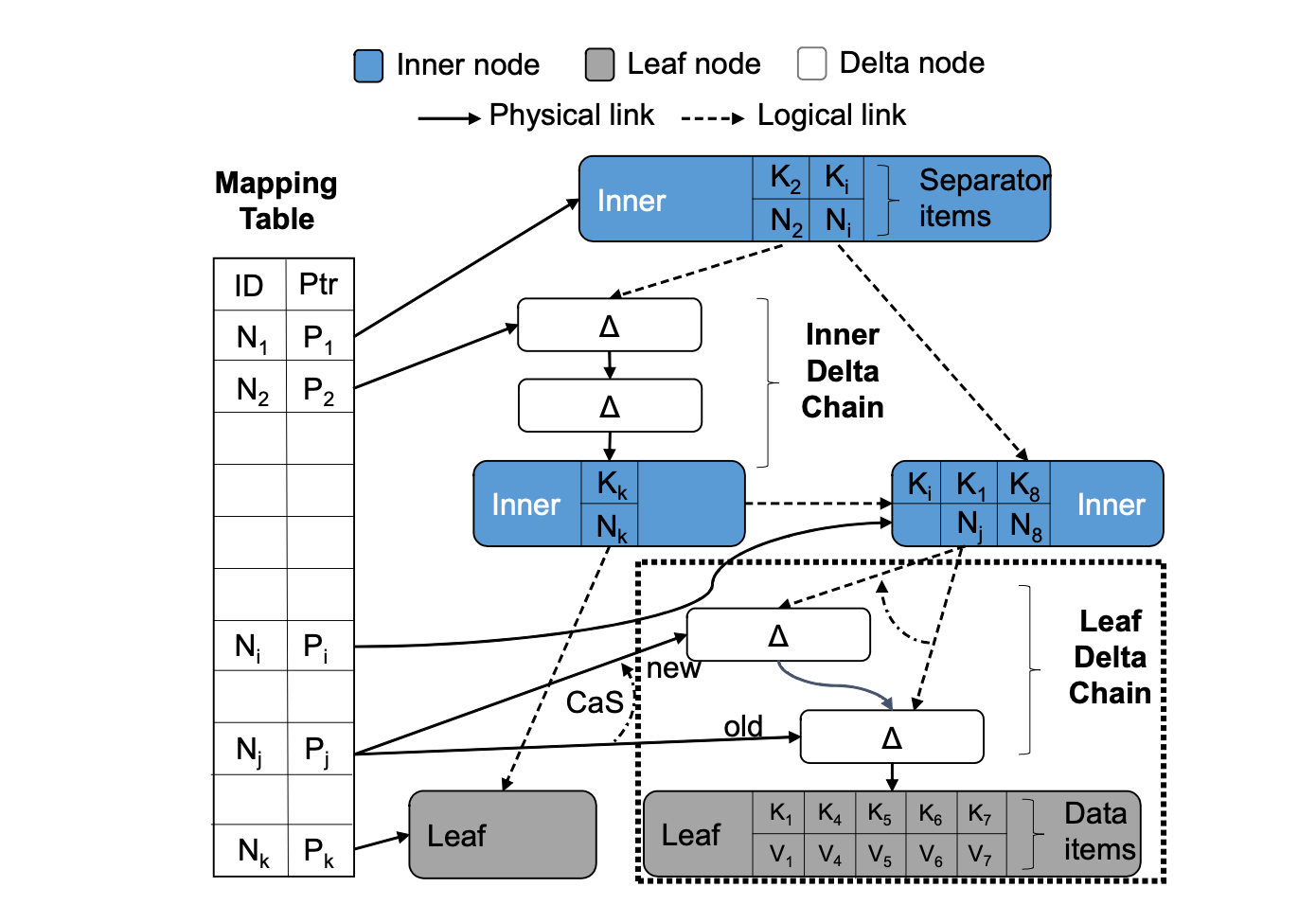
如上图所示， BW-Tree 的每个节点都有唯一的逻辑地址 PID(N1, N2, ..., Ni, ..., Nj, ..., Nk, ...) 。节点之间不使用物理地址，而是使用逻辑地址 PID 相互引用.

当需要获取某个节点的物理地址时，会先查询映射表，将 PID 转化为物理地址。 因此在对单个原子的 CAS 指令就能实现对有多个引用的节点的物理地址进行变更.

BW-Tree 和其他基于 B+tree 索引直接最大的不同在于 BW-Tree 避免直接操作树的节点，而是直接将节点的增删改查保存增量记录中，这样极大地减少了 CPU 缓存失效的概率.

另外将每个 Base Page 的变更维护在一条 增量链(Delta Chain) 中，并通过中间层映射表隔离 Page 地址的变更(PID 保持不变), 使得可以在一次原子 CAS 中实现对 Page 进行变更操作.

逻辑节点的实现细节(Base 节点和 Delta 链)

如下图所示，在 BW-Tree 中，一个逻辑节点包含两部分: Base 节点和 Delta 链。Base 节点记录当前节点的在上一次合并(consolidate) 之后的数据，Delta 链记录在此之后 Base 节点发生的所有变更操作.

Delta 链将对 Base 节点的操作按照时间顺序用单向链表(物理指针)连接起来，链表的结尾处指向 Base 节点.

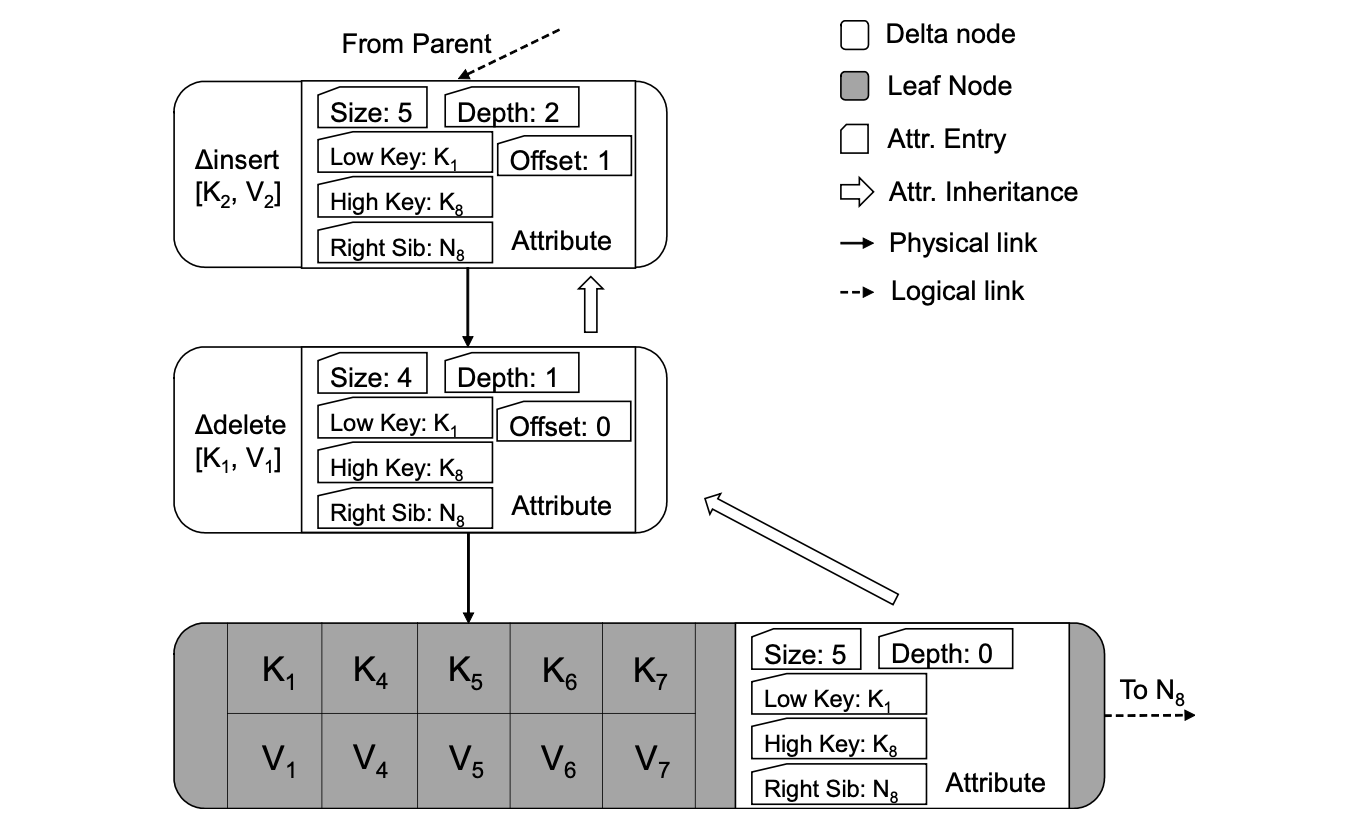
Base 节点和 Delta 链中的每一条 Delta 记录都保存了一些额外的元数据信息，它标识逻辑节点在某次操作时的状态(每次对某个节点做变更操作，都会将最新的状态记录在最新的 delta 记录中)。这些信息将会用于树的遍历等操作.

下表解释了这些元数据的内容.

• low-key , high-key ：当前逻辑节点的数据范围在区间 [low-key, high-key) 。如上图中，逻辑节点的数据范围始终未变，在每个 Delta 记录及 Base 节点中都是 [K1, K8) 。
• right-sibling : 指向右兄弟节点的逻辑地址(类似于 B-link tree)。如上图的兄弟节点 PID 为 N8 。
• size : 记录当前逻辑节点的大小。如上图中。Base 节点的 size 为 5 ；在执行完 ∆delete [K1, V1] 操作后，size 变为了 4 ；在执行完 ∆insert [K2, V2] 操作后，size 又变为了 5 。
• depth : 记录当前 Delta 记录在 Delta 链中与 Base 节点的距离。如上图中， ∆delete [K1, V1] 操作的 depth 为 1 , ∆insert [K2, V2] 操作的 depth 为 2 。
• offset ：待操作的数据在当前 Base 节点的位置(而不是逻辑节点的位置，也就是说，不关 delta 链中其他节点什么事儿)。如上图中， ∆delete [K1, V1] 操作中， K1 在 Base 节点的第一位，因此它的 offset 为 0 。 ∆insert [K2, V2] 操作中， K2 在 Base 节点的第二位，因此它的 offset 为 1 。

BW-Tree 的结构操作(Structure Modification Operation, SMO)

BW-Tree 的所有 SMO 操作都是通过原子操作实现的 latch-free 操作, 它将单个的 SMO 操作拆分为一些列 CAS 原子操作。 为了确保没有线程需要等待其他线程的 SMO 操作结束，当它发现部分完成的 SMO 操作时，会在执行当前线程原本的任务之前，先将部分完成的 SMO 操作剩下部分执行完成。(help-along protocol) 。

下面本文将会详细介绍 BW-Tree 具体是如何实现这样的能力的.

分裂(Split)

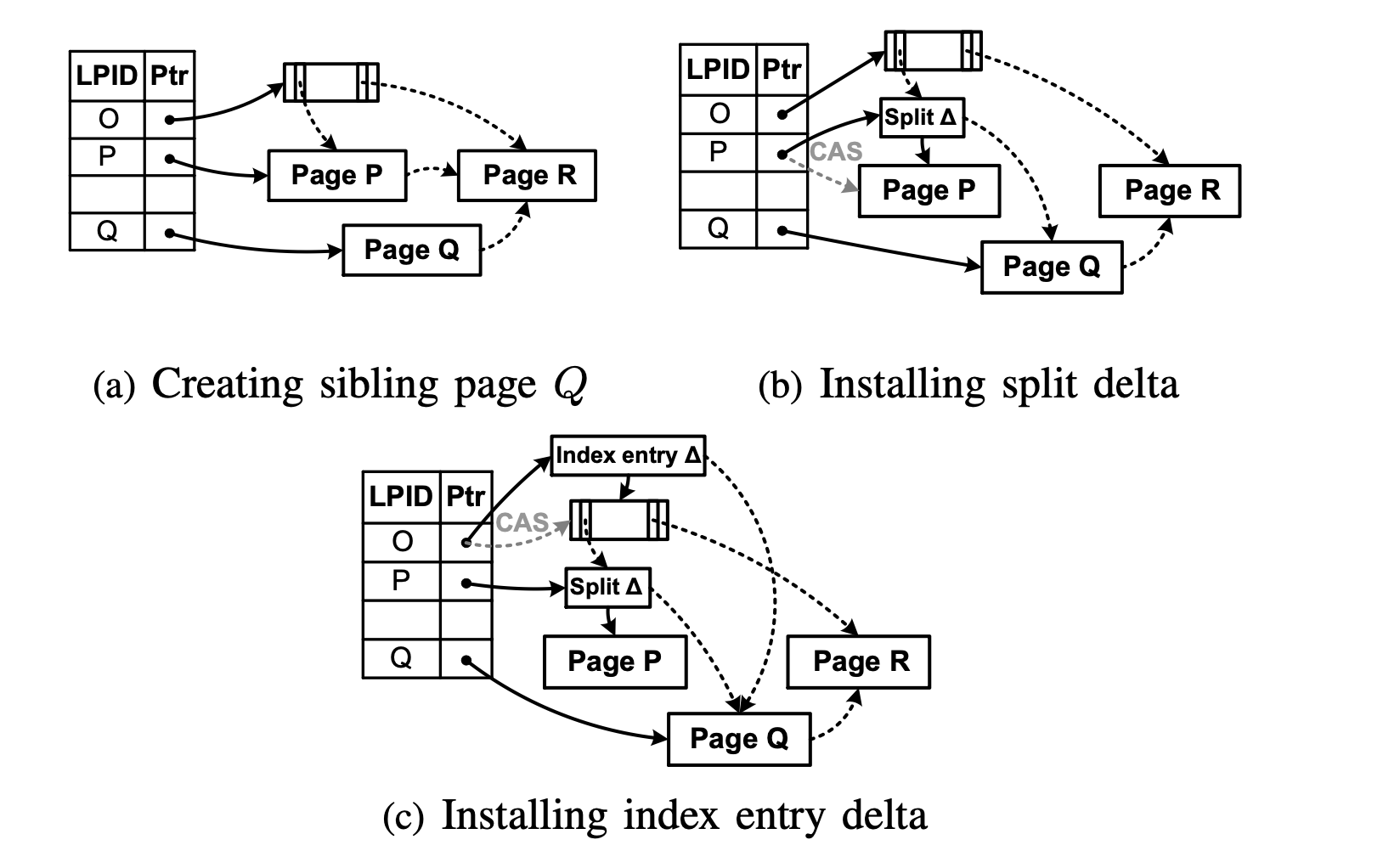
与 B-link tree 类似， BW-Tree 将 split 分为两个阶段: 先将子节点用原子操作拆分为两个节点( half split ), 然后将新的 分隔键(separator key) 和刚拆分的子节点的指针用原子操作更新到其父节点.

以上图将 O 节点的子节点 P 拆分为 P 节点和 Q 节点为例

1. 拆分子节点(half-split) (a) 创建 P 节点的兄弟节点 Q : 如上图 (a) 所示。申请一个新的 Page 作为 Q 节点；在节点 P 中找一个合适的键 Kp 作为节点 P，Q 的分隔键(separator key).

   节点 P 仅保留小于 Kp 的数据，大于等于 Kp 的数据将拷贝到节点 Q；将节点 Q 的兄弟节点设为节点 R(即当前节点 P 的兄弟节点)；将节点 Q 注册到地址映射表中.

   整个流程中，节点 Q 均不被用户可见，因此不需要原子操作。在这个阶段节点 P 依然处于为分裂状态.

   (b) 更新 P 节点, 将 Q 节点作为其兄弟节点 ：如上图 (b) 所示。为节点 P 创建执行分裂操作的 delta 记录( Split ∆ ), 该记录包含两个信息: 将 Kp 作为节点 P，Q 的分隔键以及让 Q 节点作为 P 节点的兄弟节点(让 P 逻辑节点的兄弟节点指针 right-sibling 指向 Q 节点的逻辑地址 Q)； 然后调用 CAS 原子操作将逻辑地址 P 指向 Split ∆ 的地址.

   当 CAS 操作完成时，对节点 P, Q 的所有查询，都将会被父节点 O 路由到 P 逻辑节点(Split ∆)。如果待查询的 K 小于 Kp, 查询将会被路由到节点 P。若 K 大于等于 Kp, 查询将会通过 right-sibling 路由到节点 Q.

2. 更新父节点 ：要实现直接从父节点 O 路由到刚被分裂的节点 Q(而不经过节点 P)，需要将节点 Q 的信息更新到节点 O 中。如上图 (c) 所示。 先创建一个指向节点 O 的 Delta 记录 Index entry ∆ ，它包含了三个信息: (a) 节点 P， Q 的分隔键 Kp； (b) 指向节点 Q 的逻辑地址；(c) 节点 Q 和其 right-sibling 的分隔键 Kq(Kp 和 Kq 确定出节点 Q Key 的范围 [Kp, Kq) ).

合并(Merge)

如上图所示，当某个节点的大小小于某个阈值，BW-Tree 将使用 latch-free 的方式将它合并到其他节点(BW-Tree 仅支持与左兄弟节点合并).

以上图将 P 节点的子节点 R 合并到节点 L 为例:

1. 将 R 节点标记为删除 : 如上图 (a) 所示。为节点 R 新增 Delta 记录 Remove Node ∆ , 用于将逻辑节点标记为删除。当查询访问到 Remove Node ∆ 节点，将会跳转到节点 R 左边的兄弟节点，即节点 L.

2. 合并子节点 ： 如上图 (b) 所示。为节点 L 新增 Delta 记录 Merge ∆ ，该记录将节点 L 与节点 R 合并起来作为一个逻辑节点整体.

   在步骤 1 到步骤 2 之间，实际上是无法感知到节点 R 的。(因为节点 R 已经被Remove Node ∆ 节点逻辑移除了 )。在步骤 2 执行之后， 才能通过 Remove Node ∆ 跳转到 R 的左兄弟节点 L， 通过 Merge ∆ 查询到节点 R 的值.

   但是这并不会影响并发操作的正确性，因为 help-along protocol 会保证在发现其他线程存在未完成 SMO 操作的情况下，先将 SMO 操作执行完成，再进行原本的操作。因此就不会在步骤 1 到步骤 2 之间去对节点 R 进行操作.

3. 更新父节点 : 如上图 (a) 所示。父节点添加 Delta 记录 ∆ Delete Index Term for R ，用于将节点 R 在父节点中的索引删除。节点 L 将节点 R 的索引范围也纳入其中.

   在这个阶段之后，Remove Node ∆ 这个 delta record 和节点 R 在地址映射表中的位置都将不再被使用， 他们将会被 epoch GC 逻辑回收.

点查询(Search)

• 唯一键查询 : 唯一建的查询和普通的 B+ 树类似，唯一的区别在于，当遍历到叶节点时，如果存在 Delta 链，它会先依次遍历 Delta 链，并将最先出现的结果返回。当 Delta 链中不存在时，才会去 Base 节点执行二分查找.

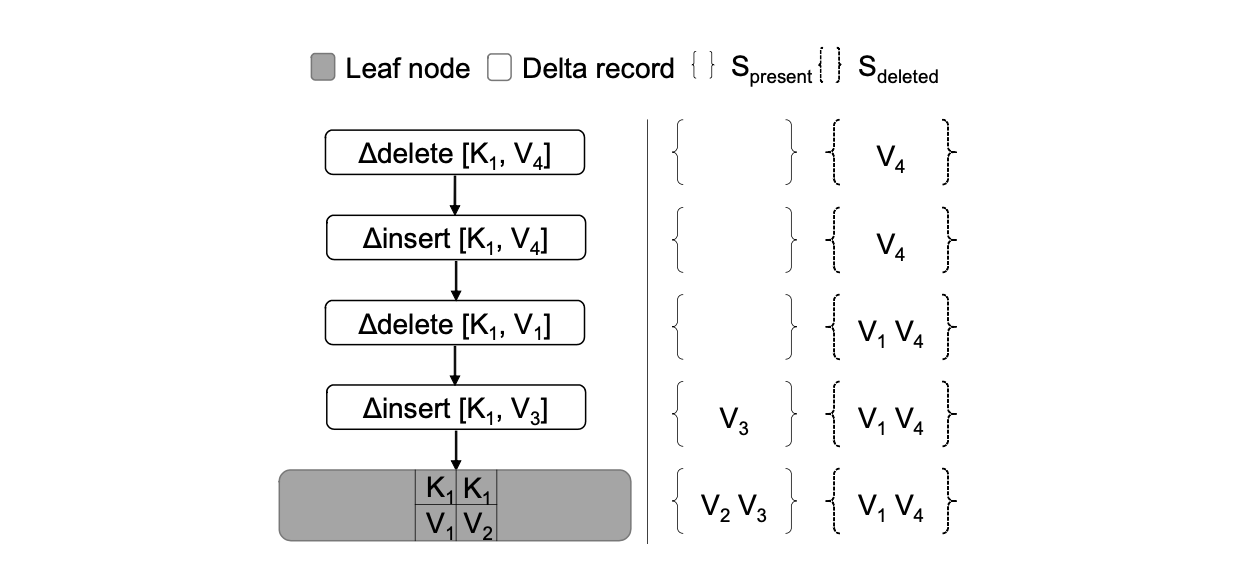
• 非唯一建查询 ：当定位到数据仅可能存在在某个叶子节点时，必须遍历所有的 Delta 链和 Base 节点才能查找出指定键的所有值。操作逻辑如下图.

  在遍历 Delta 链的过程中，将已知符合要求的数据放在集合 Spresent , 将已知被删除的数据放在集合 Sdeleted 。按顺序遍历 Delta 链时，当遍历到插入 Delta 记录(K, V) 时，如果 V 不在 Sdeleted，则将其加入 Spresent。当遍历到删除 Delta 记录(K, V) 时，如果 V 不在 Spresent，则将其加入 Sdeleted.

  记 Sbase 为 Base 节点中的该键的所有值的集合。 则最终的查询结果为 Spresent ∪ (Sbase - Sdeleted) 。

遍历(Scan)

• 正向 Scan : 正向遍历会将正在处理的节点拷贝到迭代器中。当迭代器中保存的节点的数据全部遍历完成，就会继续将下一个节点的数据全部拷贝到迭代器继续遍历。 因此，整个 Scan 过程读取的数据并不是一个快照(snapshot)的数据 .

  如下图所示，当遍历完一个节点 N0 [K0, K1) 的数据，会查找该节点的上界 K1 所在的节点作为下一个节点。 如果遍历 N0 过程中, N0 发生的 SMO 操作是的 N0 键的范围变大, 该节点的上界 K1 所在的节点依然是 N0, 则将新的 N0 拷贝到迭代器中。然后查找到 K1 的位置，继续遍历该节点.

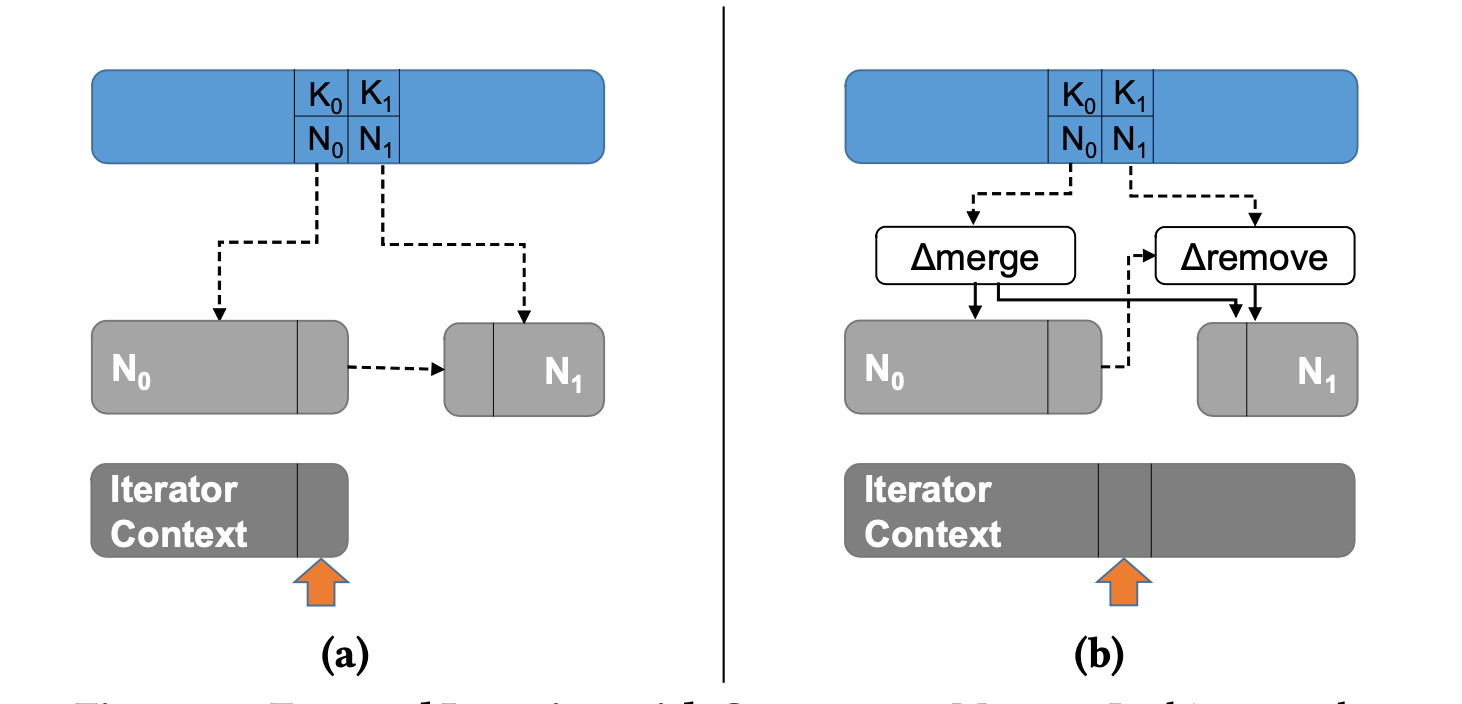
• 反向 Scan ：反向 Scan 整体逻辑和正向 Scan 一致。唯一的区别在于反向 Scan 的下一个节点的查找方式有所不同。反向 Scan 遍历完一个叶子节点后，会将小于该叶子节点的下界的最大的 Key所在的叶子节点作为下一个遍历的节点.

  如下图，N1 的下界是 K5， 小于 K5 的最大键为 K4(N0)， 因此, K4 所在的节点 N0 就是就是 N1 遍历完之后，下一个需要遍历的节点.

对 BW-Tree 的优化

• Delta 记录的预分配 : 如下图， 提前为内存中的 Delta记录预分配内存空间，减少内存碎片。

• 用去中心化 Epoch GC 替代中心化 Epoch GC

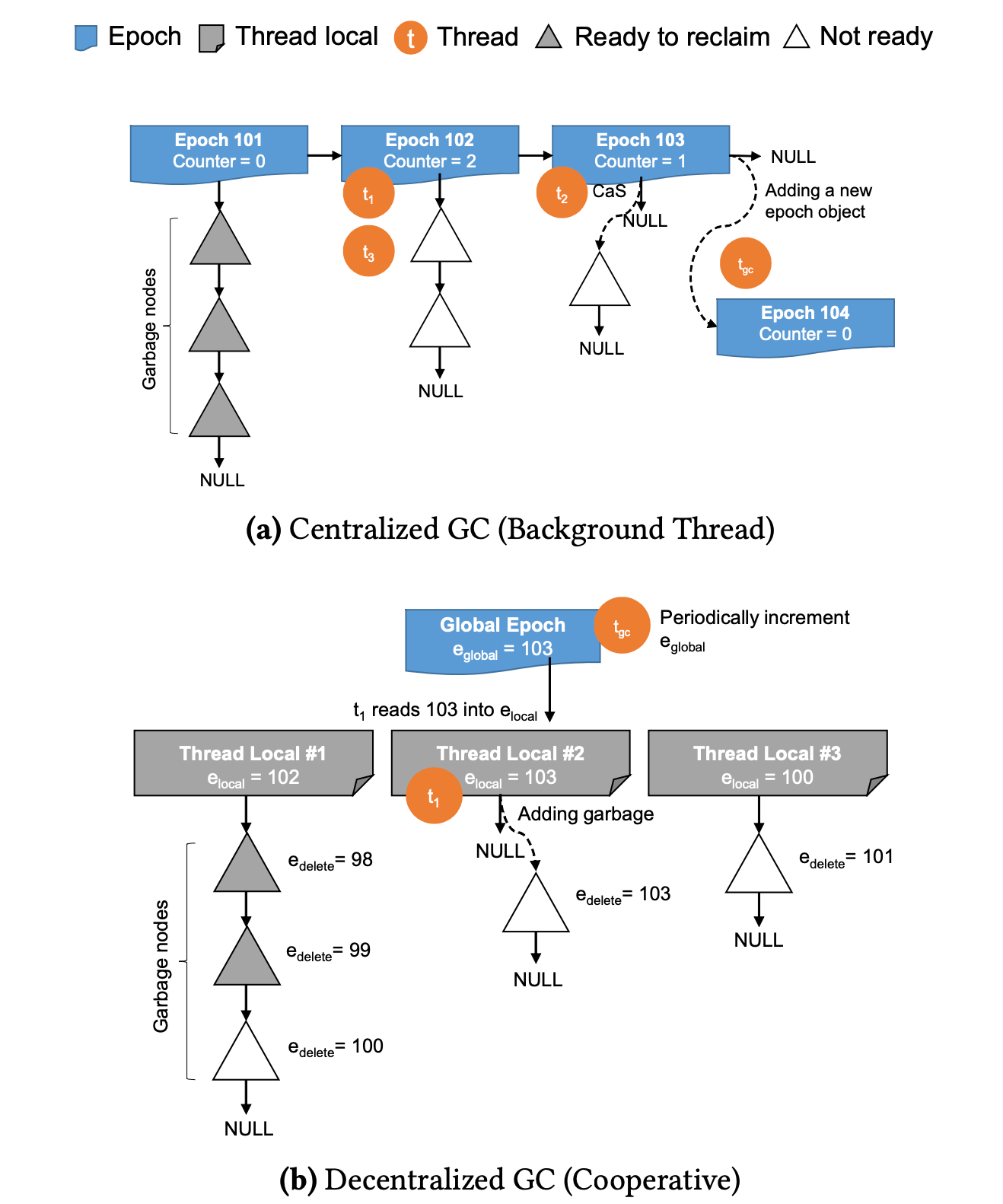
  • 中心化 Epoch GC ： 如下图 (a) 所示， 唯一的 GC 线程(Background Thread) 维护 Epoch 链表。每个 Epoch 节点维护引用当前 Epoch 删除的资源及其引用线程数的总和。当某个 Epoch 的线程引用计数恢复 0 时，该 Epoch 及其维护的垃圾资源可以被删除。如下图中的 Epoch 101.

  • 去中心化 Epoch GC ： (1) 全局 Global Epoch 维护全局 Epoch 时钟 e_global。每个工作线程产生的垃圾节点由本线程维护在本地垃圾回收链表 l_local, 并将该垃圾节点的 e_delete 设置为当前进程的 e_local.

    (2) 当某个线程开始索引操作时，会先将当前的全局 Epoch 时钟 e_global 拷贝到当前线程，记作 e_local。当该索引操作结束后，会再次将 e_local 刷新为 e_global。 (3) 每个工作现场会定期获取当前全局最小的 e_local, 并将本线程维护的 l_local 中 e_delete 小于全局最小 e_local 的垃圾节点回收.

• 快速整合(Fast Consolidation) :
  • 将原 Base 节点的键区间作为一个整体 [start, end) . 依次遍历 Delta 链，将键区间分为多个部分。
    (1) 当遍历到插入 Delta 记录，则将当前记录所在区间 [s, e) 拆分为 [s, offset) 和 [offset, e) 。
    (2) 当遍历到删除 Delta 记录，则将当前记录所在区间 [s, e) 拆分为 [s, offset) 和 [offset+1, e) 。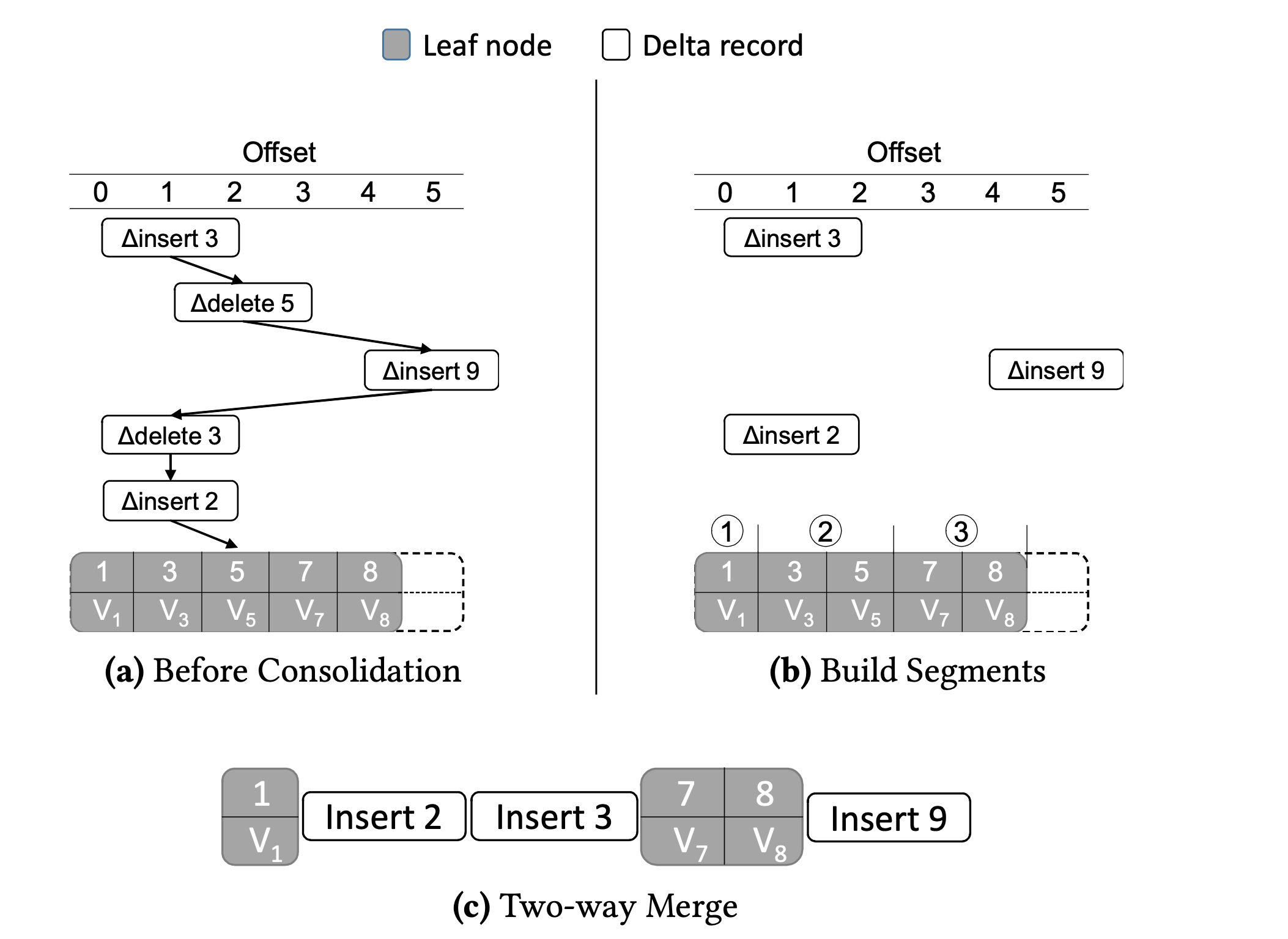
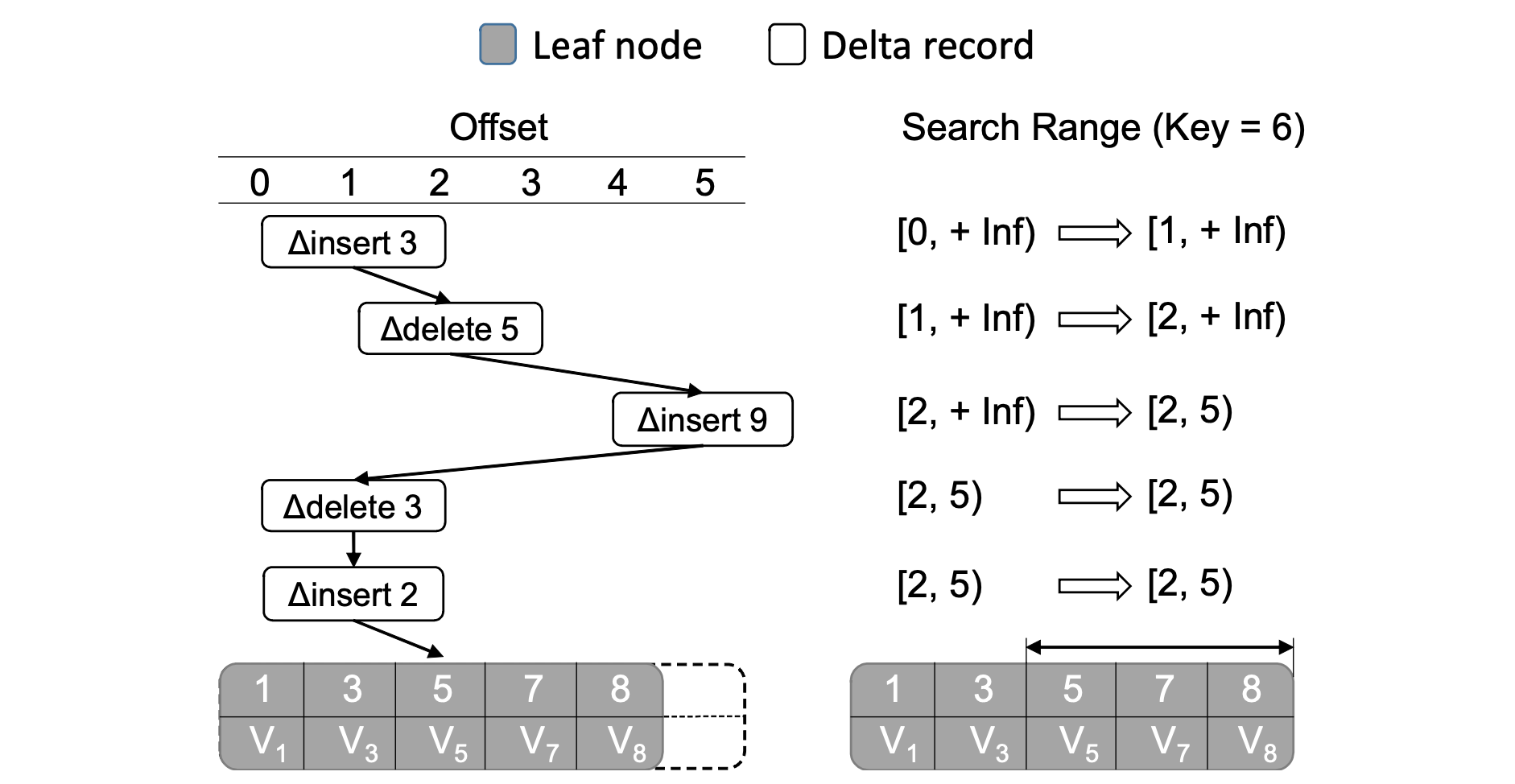
    (3) 如果删除 Delta 记录删除的数据不在 Base 节点中，则忽略该记录。
  • 上述操作将 Base 节点拆分为多个部分。然后将拆分的多个部分和新插入数据一起整合成新的 Base 节点。

• 节点搜索快捷方式(Node Search Shortcuts)

  • 当工作线程遍历 Delta 链查找键 K 时， 它会初始化二分查找的偏移量(offset) [min. max) 范围为 [0, +inf) 。遍历过程中，当遇到键位 K', 偏移量为 offset 的 ∆insert 或 ∆delete 记录，它会比较 K 与 K'。若 K=K', 则立即得到 K 所在偏移量为 `[offset, offset+1)``，不用在 Base 节点进行二分查找。若 offset > min 并且 K>K′， 则将 min 设为 offset。 若 offset < max 并且 K <K′， 将 max 设为 offset。如果最后的区间大小大于 1， 则在偏移量区间内二分查找键 K.

  • 如下图中的例子， 最终得到的区间是 [2, 5) , 因此最后只需要在 Base 节点中 offset 在 [2. 5) 区间内的键二分查找 Key=6.

其他

本文更多的是介绍内存内的 BW-Tree 的维护逻辑，更多关于持久化数据的维护相关的内容请查看 LLAMA: A Cache/Storage Subsystem for Modern Hardware 。后续我也会在公众号 IT技术小密圈 更新对该论文的分享，欢迎关注.

参考文献

• Building a Bw-Tree Takes More Than Just Buzz Words
• The Bw-Tree: A B-tree for New Hardware
  Platforms
• LLAMA: A Cache/Storage Subsystem for Modern Hardware

参考文献可能不太好下载。如果你获取不到这几篇论文，可以关注公众号 IT技术小密圈 回复 bw-tree 获取.

最后此篇关于【技术分享】万字长文图文并茂读懂高性能无锁“B-Tree改”：Bw-Tree的文章就讲到这里了,如果你想了解更多关于【技术分享】万字长文图文并茂读懂高性能无锁“B-Tree改”：Bw-Tree的内容请搜索CFSDN的文章或继续浏览相关文章，希望大家以后支持我的博客！ 。