初等数论

素数定义

设整数 \(p\ne 0,\pm 1\) 。如果 \(p\) 除了平凡约数以外没有其他约数，那么称 \(p\) 为素数（不可约数）.

若整数 \(a\ne 0,\pm 1\) 且 \(a\) 不是素数，则称 \(a\) 为合数.

——————OI Wiki 。

素数的判定（素性测试）

如何判断一个数 \(x\) 是不是质数?

很显然我们可以暴力的枚举 \(1\) 到 \(\sqrt{x}\) 来看是否整除来判断，但复杂度太高了.

                        
                          #include<bits/stdc++.h>
#define int long long 
using namespace std;
int t,n;
inline int pd(int x)
{
    int len=sqrt(x);
    for(int i=2;i<=len;i++)
        if(x%i==0)return 0;
    return 1;
}
signed main()
{
    cin>>t;
    while(t--)
    {
        cin>>n;
        if(pd(n))cout<<"Y"<<endl;
        else cout<<"N"<<endl;
    }
    return 0;
}

                        
                      

Miller-Rabin素性测试

这个算法就一个用法：判断一个数是不是素数.

这个算法的依据是:

费马小定理

对于任意的质数 \(p\) ,任意整数 \(a\) ,均满足: \(a^{p}\equiv a\pmod{p}\) ，如果 \(a\) 不是 \(p\) 的倍数，这个也可以写成 \(a^{p-1} \equiv 1 \pmod{p}\) 。

证明如下: 这个式子可以用欧拉定理来证明

首先,把式子稍微变换一下得到

\(a^{p-1}\times a\equiv a\pmod{p}\) ,因为 \(a\equiv a\pmod{p}\) 恒成立,所以 \(a^{p-1}\bmod p=1\) 时费马小定理才成立,又因为 \(p\) 是质数,所以 \(\varphi(n)=n-1\) ,所以根据欧拉定理:若 \(a\) , \(p\) 互质则 \(a^{p-1}\bmod p=1\) 成立。那么对于 \(a\) , \(p\) 不互质，因为 \(p\) 是质数，所以， \(a\) 一定是倍数 \(a^{p}\equiv a\equiv 0 \pmod{p}\) 。综上所述，费马小定理得证，其实算是一个欧拉定理的特例.

那么是不是当一个数 \(p\) 满足任意 \(a\) 使得 \(a^{p-1}\equiv \pmod{p}\) 成立的时候它就是素数呢?

答案是 false 。

所以我们需要下面的定理来减小错误的概率.

二次探测定理

若 \(p\) 为素数， \(a^{2}\equiv \pmod{p}\) ，那么 \(a\equiv \pm 1\pmod{p}\) 。

证明:

\(a^{2}\equiv 1\pmod{p}\) 。

\(a^{2}-1\equiv 0\pmod{p}\) 。

\((a-1)\times (a+1)\equiv 0\pmod{p}\) 。

\((a-1)\equiv 0\pmod{p}\) 或 \((a+1)\equiv 0\pmod{p}\) 。

\(a\equiv \pm 1\pmod{p}\) 。

算法过程

我们把 \(p-1\) 分解成 \(2^{k}\times t\) 的形式 。

能这么分的原因是 \(p\) 如果是素数，那他只要不是 \(2\) ，那么 \(p-1\) 一定是偶数，也就是都至少能分离出一个二出来 。

当 \(p\) 是素数，有 \(a^{2^{k}\times t}\equiv 1\pmod{p}\) 。

然后随机选择一个数 \(a\) ，计算出 \(a^{t}\pmod{p}\) 。

然后如果要是当前的值就是 \(1\) ，那么说明后面再平方也还是 \(1\) （二次探测定理），可以直接返回判断是素数；否则就开始跟据计算出来的 \(k\) 来进行 \(k\) 次的平方操作，如果要是遇到值为 \(p-1\) 的值，下一次平方值必定为 \(1\) ，所以也可以直接返回，这样就实现了利用费马小定理的同时利用二次探测定理来判断素数了 。

百度告诉我们若 \(p\) 通过一次测试，则 \(p\) 不是素数的概率为 \(25\%\) 。

那么我们用 \(2,3,5,7,11,13,17,19,23,27...\) 来进行多次判断，正确性就会大大提高.

当然也不会是 \(100\%\) ，但是有以下的结论.

我们需要注意的是，因为是次方运算有点猛，所以推荐使用龟速乘来防止溢出.

埃氏筛

从小到大枚举范围，如果当前数没有被标记就说明是质数，直接加进去，然后枚举在范围内的当前数的倍数标记，然后一直重复直到结束，算是比较优秀的筛了（至少相对暴力）据说复杂度 \(O(n\log\log n)\) 。

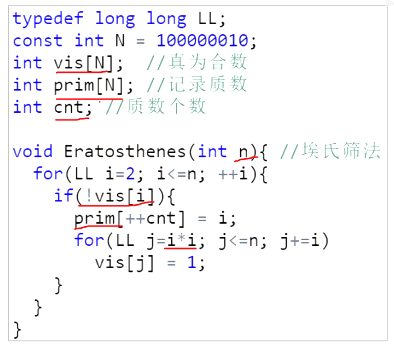
图片来自 b 站董晓算法.

线性筛

重中之重，必须掌握——————我说的 。

当然我觉得这个还是更快一些的.

我们首先要知道的就是上面的筛慢在什么地方?

因为有很多数被重复筛了好几次，那么我们有什么办法能不能让一个数只被筛一次，让复杂度成为真正的线性呢?

答案是 true 。

我们和上面一样，只不过在筛的时候，我们不是枚举当前质数的多少倍了，而是每枚举到一个数 \(i\) ，然后就开始枚举当前筛出来的质数的 \(i\) 倍，而当当前 \(i\) 对当前枚举到的质数取模是 \(0\) 的时候，就直接退出，这样可以做到每一个合数都被自己的最小质因数筛掉，因为当前 \(i%p=0\) 说明 \(i\) 已经被 \(p\) ，也就是 \(i\) 的最小质因数给筛掉了，那么后面在出现的 \(i\) 乘以各个素数的数一定会被 \(p\) 给筛掉，现在就不用筛了，直接退出.

code

                        
                          #include<bits/stdc++.h>
using namespace std;
int n,m,ans[100010000],vis[100010000],cnt;
int main()
{
	std::ios::sync_with_stdio(0);
	cin>>n>>m;
	for(int i=2;i<=n;i++)
	{
		if(!vis[i])ans[++cnt]=i;
		for(int j=1;j<=cnt&&ans[j]*i<=n;j++)
		{
			vis[ans[j]*i]=1;
			if(i%ans[j]==0)break;
		}
	}
	for(int i=1;i<=m;i++)
	{
		int x;
		cin>>x;
		cout<<ans[x]<<endl;
	}
	return 0;
}

                        
                      

EXGCD

欧几里得应该在上一篇关于数论的文章里讲到了，而且也不难，所以在此不再赘述.

基本算法：对于不完全为 \(0\) 的非负整数 \(a\) , \(b\) , \(\gcd(a,b)\) 表示 \(a\) , \(b\) 的最大公约数，必然存在整数对 \(x\) , \(y\) ，使得 \(\gcd(a,b)=a\times x+b\times y\) . 。

证明:

设 \(a>b\) . 。

显然当 \(b=0,\gcd(a,b)=a\) ,此时 \(x=1,y=0\) . 。

当 \(a\times b \ne 0\) 时； 。

设 \(a\times x_{1}+b\times y_{1}=\gcd(a,b)\) ,

\(b\times x_{2}+(a\bmod b)\times y_{2}=\gcd(b,a\bmod b)\) 。

根据朴素的欧几里得原理有 \(\gcd(a,b)=gcd(b,a\bmod b)\) ,

则： \(a\times x_{1}+b\times y_{1}=b\times x_{2}+(a\bmod b)\times y_{2}\) 。

即： \(a\times x_{1}+b\times y_{1}=b\times x_{2}+(a-\left \lfloor\frac{a}{b}\right \rfloor\times b)\times y_{2}=a\times y_{2}+b\times x_{2}-\left \lfloor\frac{a}{b}\right \rfloor\times b\times y_{2}\) 。

等量代换得： \(x_{1}=y_{2};y_{1}=x_{2}-\left \lfloor\frac{a}{b}\right \rfloor\times y_{2}\) ,

这样我们就可以一直递归求 \(x1,y1\) 了.

因为总有一个时候 \(b=0\) ，所以递归可以结束.

                        
                          #include<bits/stdc++.h>
#define int long long 
using namespace std;
int x,y,n,m;
inline void exgcd(int a,int b)
{
	if(b==0){x=1,y=0;return ;}
	exgcd(b,a%b);
	int t=x;
	x=y;
	y=t-a/b*y;
}
signed main()
{
	cin>>n>>m;
	exgcd(n,m);
	x=(x%m+m)%m;
	cout<<x<<endl;
	return 0;
}

                        
                      

或者这种写法:

                        
                          #include<bits/stdc++.h>
#define int long long 
using namespace std;
int x,y,n,m;
inline void exgcd(int a,int b,int &x,int &y)
{
	if(b==0){x=1,y=0;return ;}
	exgcd(b,a%b,y,x);
	y-=a/b*x;
}
signed main()
{
	cin>>n>>m;
	exgcd(n,m,x,y);
	x=(x%m+m)%m;
	cout<<x<<endl;
	return 0;
}

                        
                      

逆元

主要还是模运算下乘法运算的逆元， 下文中逆元都会带有下标 \(inv\) .

如果一个线性同余方程 \(ax\equiv 1\pmod{b}\) ，则称 \(x\) 为 \(a\bmod b\) 的逆元，记作 \(a^{-1}\) 。 ——————OI Wiki 。

EXGCD求逆元

\(a \equiv b \pmod{m}\) 。

老朋友了，表示 \(a\bmod m=b\mod m\) .

然后看一下这个： \(\frac{a}{b} \equiv x\pmod{p}\) . 。

模意义下的除法在大多数时候都不适用.

当题目中要求对答案取模，但我们又不得不使用一般的除法的时候，就需要用逆元的乘法来代替除法.

根据逆元的定义得:

\((a\times b_{inv}) \equiv x \pmod{p}\) ,

左右两边同乘 \(b\) ,移项得:

\(\left\{\begin{matrix} (b\times a\times b_{inv})\equiv x\times b \pmod{p}\\ a\equiv b\times x \pmod{p} \end{matrix}\right.\) 。

上减下得:

\(a\times(b\times b_{inv}-1)\equiv 0 \pmod{p}\) 。

移项得:

\(b\times b_{inv}-1\equiv 0 \pmod{p}\) ,

两边同时加一得:

$ b\times b_{inv}\equiv 1\pmod{p}$； 。

设一个正整数 \(k\) ； 。

两边同时加 \(k\times p\) 得； 。

$ b\times b_{inv}+k\times p\equiv 1+k\times p\pmod{p}$； 。

因为 \((k\times p )\bmod p=0\) ,

所以：$ b\times b_{inv}+k\times p\equiv 1\pmod{p}$； 。

根据我们的扩展欧几里得可以得知：当知道 \(a,b\) 的值的时候是可以求出 \(a\times x+b\times y=gcd(a,b)\) 中的 \(x,y\) 的值。当然前提是 \(b,p\) 互质的时候上面的柿子就可以得出:

\(b\times b_{inv}+k\times p= 1\) ； 。

知道 \(b,p\) 就可以愉快的求 \(b_{inv}\) 啦.

好的到了这一步已经可以有两种解决方式了，一种是用扩展欧几里得来解逆元，另一种是用费马小定理，先来好理解的.

费马小定理求逆元

首先回到我们前面推的柿子； 。

$ b\times b_{inv}\equiv 1\pmod{p}$； 。

好的现在我们可以知道当 \(p\) 为质数时:

\(a^{p}\equiv a\pmod{p}\) ,

稍微变换一下得:

\(a^{p-1}\times a\equiv a\pmod{p}\) 。

因为 \(a\) 是正整数，两边同除 \(a\) 得:

\(a^{p-1}\equiv 1 \pmod{p}\) ,

根据我们上面得出得柿子一结合就可以得出:

\(\left.\begin{matrix} b\times b_{inv}\equiv 1\pmod{p} \\ b\times b^{p-2}\equiv 1\pmod{p} \end{matrix}\right\}\Rightarrow b_{inv}=b^{p-2}\) 。

所以我们就可以用:

\(a\times b^{p-2} \bmod p\) 来求 $ \frac{a}{b}\bmod p$ 啦.

线性求逆元

前面的都太慢了，我们要追求效率.

首先我们有一个 \(1_{inv}\equiv 1\pmod{p}\) ,

我们设 \(p=k\times i+r\) ； 。

然后放到 \(\pmod{p}\) 意义下就可以得到:

\(k\times i+r\equiv 0\pmod{p}\) ,

乘上 \(i_{inv},r_{inv}\) 可以得到,

\(k\times r_{inv}+i_{inv}\equiv 0\pmod{p}\) 。

移项得:

\(i_{inv}\equiv -k\times r_{inv}\pmod{p}\) 。

把 \(k,r_{inv}\) 用 \(p\) 表示出来就好了.

\(i_{inv}\equiv -\left \lfloor \frac{p}{i} \right \rfloor \times (p\bmod i)_{inv} \pmod{p}\) ,

贴一下代码:

                        
                          inv[1] = 1;
for(int i = 2; i < p; ++ i)
    inv[i] = (p - p / i) * inv[p % i] % p;


                        
                      

积性函数

数论函数：在数论上，对于定义域为正整数，值域为复数的函数，我们称之为数论函数.

非完全积性函数：对于数论函数 \(f\) ，若满足 \(gcd(a,b)=1\) 时，有 \(f(ab)=f(a)\times f(b)\) ，则称函数 \(f\) 为积性函数. 。

完全积性函数：对于数论函数 \(f\) ，即使不满足 \(gcd(a,b)=1\) ，仍有 \(f(ab)=f(a)\times f(b)\) ，则称函数 \(f\) 为完全积性函数. 。

简单积性函数

\(\varphi (n)\) ————欧拉函数，计算从一到 \(n\) 与 \(n\) 互质的数的数目.

\(\mu(n)\) ————莫比乌斯函数，关于非平方数的质因子数目. 。

\(\mu(n)=\left\{\begin{matrix} 1 \ \ (n=1) \\ 0\ \ \ \ (n\text{含有1除外的平方因子}) \\ (-1)^{k}\ \ \ \ (k\text{为}n\text{的本质不同质因子个数）} \end{matrix}\right.\) 。

\(\gcd(n,k)\) ————最大公约数函数，当 \(k\) 固定的情况时是积性函数.

\(d(n)\) ———— \(n\) 的正因子数目.

\(\sigma(n)\) ———— \(n\) 的正因子之和.

\(\sigma k(n)\) ————因子函数， \(n\) 的所有正因子的 \(k\) 次幂之和，当中 \(k\) 可以为任何复数.

\(1(n)\) ————不变的函数，定义为 \(1(n)=1\) （完全积性函数）.

\(id(n)\) ————单位函数，定义为 \(id(n)=n\) （完全积性函数）.

\(idk(n)\) ————幂函数，对于任何复数、实数 \(k\) ，定义为 \(idk(n)=n^k\) （完全积性函数）.

\(\xi(n)\) ————定义为：若 \(n=1\) , \(\xi(n)=1\) ;若 \(n>1,\xi(n)=0\) 。别称为“对于狄利克雷卷积的乘法单位”（完全积性函数）.

\(\lambda(n)\) ————刘维尔函数，关于能整除 \(n\) 的质因子的数目. 。

\(\gamma(n)\) ————定义为 \(\gamma(n)=(-1)^{\omega(n)}\) ,在此加性函数 \(\omega(n)\) 是不同能整除 \(n\) 的质数的数目.

参考资料：OI WIKI，自为风月马前卒的博客， https://www.cnblogs.com/zylAK/p/9569668.html ，b站董晓算法.

最后此篇关于初等数论——素数，逆元，EXGCD有关的文章就讲到这里了,如果你想了解更多关于初等数论——素数，逆元，EXGCD有关的内容请搜索CFSDN的文章或继续浏览相关文章，希望大家以后支持我的博客！ 。