个人中心
文章发布
退出
作者热门文章
- Java锁的逻辑（结合对象头和ObjectMonitor）
- 还在用饼状图？来瞧瞧这些炫酷的百分比可视化新图形（附代码实现）⛵
- 自动注册实体类到EntityFrameworkCore上下文，并适配ABP及ABPVNext
- 基于Sklearn机器学习代码实战
26
4
最近在备考软考的软件设计师考试，学到了关于计算机的数据表示，由于我是半路出家学的Java，导致计算机基础知识很差，在这里记录一下学习感受 。
更详细的请参考 计算机为啥采用二进制 。
首先，假如你的计算机是32位的机器，数字 1 在计算机中的表示就是 0000000000000000001 , 假如你是要操作内存，用这么长一串二进制数，是不是感觉有点头大，1位16进制数可以表示4位二进制数， 那 数字1用16进制 来表示就是 1H ，是不是感觉清爽多了.
阅读本章之前需要明确的点 。
对于10进制转其他进制，一般是使用除法取余数的方式进行计算 。
例如将数字 151 转换为二进制 。
被除数 ÷ 除数 = 商 ... 余数
151 ÷ 2 = 75 ... 1
75 ÷ 2 = 37 ... 1
37 ÷ 2 = 18 ... 1
18 ÷ 2 = 9 ... 0
9 ÷ 2 = 4 ... 1
4 ÷ 2 = 2 ... 0
2 ÷ 2 = 1 ... 0
1 ÷ 2 = 0 ... 1
将每一步得到的余数从下往上依次排列，得到 10010111，即151的二进制表示。
转为八进制 。
151 ÷ 8 = 18 ... 7
18 ÷ 8 = 2 ... 2
2 ÷ 8 = 0 ... 2
151的8进制表示为227
转为十六进制 。
151 ÷ 16 = 9 ... 7
9 ÷ 16 = 0 ... 9
因此，151的16进制数为97
对于其他进制转换为10进制，我们一般是采用按权展开法，并且具有公式 。
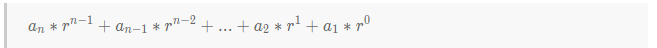
例如: 十进制数 11 的二进制数为 1011 。
使用按权展开法,首先该二进制数有 4位 ，所以 n为4 ,可以得出以下式子 。
对于八进制，十六进制都是使用该方法转换为10进制 。
将二进制数转换为八进制数，需要先将二进制数转换为10进制，然后将10进制数转换为八进制 。
这种转换方式有点麻烦，如果不是很大的数字，可以看下一章，快速转换 。
快速转换可以通过查表的方式快速转换 。
| 十进制 | 二进制 | 八进制 | 十六进制 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | - | 8 |
| 9 | 1001 | - | 9 |
| 10 | 1010 | - | A |
| 11 | 1011 | - | B |
| 12 | 1100 | - | C |
| 13 | 1101 | - | D |
| 14 | 1110 | - | E |
| 15 | 1111 | - | F |
在这个表格中，每个进制的数字都有对应的二进制、八进制、十进制、十六进制数。例如，十进制数2对应二进制数10，八进制数2和十六进制数2都是用数字2来表示，十六进制数F对应二进制数1111。使用这个表格可以快速地进行不同进制之间的转换.
这种方式对于二进制、八进制、十六进制之间的转换非常有效 。
例如 将二进制数10101转换为十六进制 。
还记得小学我们学的十进制加减法不，即 满十进一法 . 其实对于二进制，八进制，16进制数可分别对应满二进一，满八进一，满16进一. 。
请参考 16进制加减法 。
学习该章首先要明确的点 。
首先假如我们在一个 字长为8位 的计算机中进行运算 5 + 7 。
将它们转换为2进制运算 00000101 + 00000111 = 00001100 00001100 = 12 。
那假如是 -5 + -7 呢 。
转换为二进制运算就是，10000101 + 10000111 = 100001100 。
100001100 计算出来的二进制数变成了9位，8位下的计算计算机咋能表示9位呢，那把 首位的1去掉 就变成了00001100 = 12 。
额，为啥 两个负数相加咋变成正数了，计算机是不是傻了。我们下节继续 。
最后此篇关于程序员不得不了解的计算机进制转换的文章就讲到这里了,如果你想了解更多关于程序员不得不了解的计算机进制转换的内容请搜索CFSDN的文章或继续浏览相关文章，希望大家以后支持我的博客！ 。
26
4
0
在 PHP 中，开始破解并弄清楚页面上发生的事情非常容易。只需输入一堆回声和 print_r，仅此而已。看来这种技术在 python 中对我不起作用。我通过在 python 照片上传模块中进行黑客攻击
程序员/后端开发方向Java 跳槽注意事项（简历和面试经验分享） 应届生面试经验参考：https://www.cnblogs.com/rainbow-1/p/16779048.html 简历： 1、
上图的意思： 百战百胜，屡试不爽. 故事 程序员小张： 刚毕业，参加工作1年左右，日常工作是CRUD 。 架构师老李： 多个大型项目经验，精通各种开发架构屠龙宝术；
周末了开心一下 谈到程序员，对于外行人来说一贯的印象就是格子衫大裤衩外加人字拖，蓬头（秃头）垢面黑眼圈，还有就是“人傻钱多死得快”🤣，这是外界对程序员固有的思想，但是作为新世纪的程序员，我们可没那么
我从事C++编程已有5年了，现在我意识到知道如何“不同地”思考的值(value)。 这个问题适用于尝试其他编程语言并遇到过类似情况的C++程序员: “哇，这太酷了!我不知道我可以那样编程。” “哇，我
互联网已经渗入我们生活的方方面面，于是我们就免不了会思考：如果有一天网络断了怎么办呢? 英国 Cable.co.uk 曾进行了一项有趣的"断网"调查，调查发现在 2500
这些是 “程序员可见” x86-64 寄存器: (来源:usenix.org) 隐形寄存器呢？刚刚才知道MMU寄存器，Interrupt Descriptor Table(IDT)使用了这些不可见的寄
关闭。这个问题是opinion-based .它目前不接受答案。 想要改进这个问题？ 更新问题，以便 editing this post 可以用事实和引用来回答它. 关闭 9 年前。 Improve
有没有办法将 Dragon NaturallySpeaking 合并到事件驱动程序中？如果我使用 DNS 记录用户语音输入而不将其写入屏幕并直接保存为 XML，我的老板会非常喜欢它。我已经研究了好几天
按照目前的情况，这个问题不适合我们的问答形式。我们希望答案得到事实、引用或专业知识的支持，但这个问题可能会引发辩论、争论、投票或扩展讨论。如果您觉得这个问题可以改进并可能重新打开，visit the
关闭。这个问题不符合Stack Overflow guidelines .它目前不接受答案。 这个问题似乎与 help center 中定义的范围内的编程无关。 . 关闭 8 年前。 Improve
按照目前的情况，这个问题不适合我们的问答形式。我们希望答案得到事实、引用或专业知识的支持，但这个问题可能会引发辩论、争论、投票或扩展讨论。如果您觉得这个问题可以改进并可能重新打开，visit the
关闭。这个问题是opinion-based .它目前不接受答案。 想要改进这个问题？ 更新问题，以便 editing this post 可以用事实和引用来回答它. 关闭 9 年前。 Improve
这个问题在这里已经有了答案: 关闭12年前。 Possible Duplicate: Should I learn C before learning C++? 作为一名专业 (Java) 程序员和重
关闭。这个问题不满足Stack Overflow guidelines .它目前不接受答案。 想改善这个问题吗？更新问题，使其成为 on-topic对于堆栈溢出。 6年前关闭。 Improve thi
就目前而言，这个问题不适合我们的问答形式。我们希望答案得到事实、引用资料或专业知识的支持，但这个问题可能会引发辩论、争论、投票或扩展讨论。如果您觉得这个问题可以改进并可能重新打开，visit the
很难说出这里问的是什么。这个问题是含糊的、模糊的、不完整的、过于宽泛的或修辞性的，无法以目前的形式得到合理的回答。如需帮助澄清此问题以便重新打开它，visit the help center 。 已关
就目前而言，这个问题不适合我们的问答形式。我们希望答案得到事实、引用资料或专业知识的支持，但这个问题可能会引发辩论、争论、投票或扩展讨论。如果您觉得这个问题可以改进并可能重新打开，visit the
我正在将一个使用串行端口的 C++ 程序(更准确地说是 Borland“组件”)“转换”为 Java。该程序使用一个线程来监听串行端口，并在收到给定的“事件字符”之一(可能是回车、ACK、NACK .
我是克里斯。我对编码很陌生，我不知道很多术语，这是我第三次也是最成功的学习 Java 的尝试。是的，如果我还年轻，效果就不太好。无论如何，我正在尝试创建游戏，但遇到了一个小问题。 我制作了一个 16
我是一名优秀的程序员,十分优秀！