最长递增子序列

力扣题目链接(opens new window) 。

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度.

子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列.

示例 1:

• 输入：nums = [10,9,2,5,3,7,101,18]
• 输出：4
• 解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。

示例 2:

• 输入：nums = [0,1,0,3,2,3]
• 输出：4

示例 3:

• 输入：nums = [7,7,7,7,7,7,7]
• 输出：1

提示:

• 1 <= nums.length <= 2500
• -10^4 <= nums[i] <= 104

思路

什么是" 最长递增子序列 "?

以 nums = [1,8,3,2,5,6,7,9] 为例 。

[1,8]是nums中的一个"递增子序列"，[3,5,6]是另一个"递增子序列"，且后者更长 。

由上述例子可知，子序列的选取可以不连续，但必须按照数组原有顺序来取（意思就是可以在原有顺序上跳过某些数从而构成更长的子序列） 。

基于此原则，上述例子中的"最长递增子序列"是[3,5,6,7,9] 。

明确这一点后，可以开始讨论解题方法 。

五步走

1、2 确定dp数组含义+确定递推公式

dp[i]: 以nums[i]为结尾 的最长递增子序列 的长度 。

这么理解呢?

举个例子，nums = [1,8,3,2,5,6] 。

遍历时是用双指针去实现子序列的查找的，因此还需要一个指针j用来遍历区间内的所有元素，寻找该区间内最长的子序列 。

假设j是小于i的 ，那么两者构成的区间就是[j,i] 。

此时就有dp[j] < dp[i]，即以nums[0]为结尾的最长递增子序列（即[1]）小于以nums[1]为结尾的最长递增子序列（即[1,8]） 。

此时，指针i向后移动，j也继续在[j,i]范围内遍历，当遍历到以下位置时，可以找到 推导出dp[i]的前置位置 。

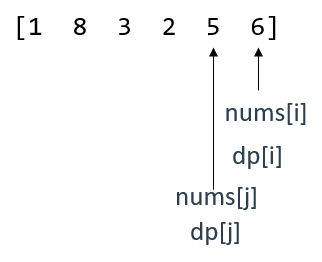
当前，dp[j]仍小于dp[i]（len[1,3,5] < len[1,3,5,6]），根据dp数组的定义，dp[j]是"长度".

就这个层面而言，dp[i]与dp[j]的长度差距为1，所以有 dp[i] = dp[j] + 1,

上面说过，指针j是在[j,i]范围内从左向右遍历，目的是寻找子序列 。

因此每次遍历都会得到一个新的dp[i] 。

所以递推公式应该是： dp[i] = max(dp[i], dp[j] + 1),

这里解释一下在遍历过程中，子序列是如何定义的，以及我们比较dp[i]和dp[j]到底在比较什么东西 。

因为i和j都是从左往右遍历，所以每次循环以nums[i]和以nums[j]为结尾的最长递增子序列都有可能更新 。

不同的是，指针j的遍历范围是约束在[j,i]之内的 。

每次遍历完[j,i]之内的 所有子序列nums[j] 后，才会移动i去扩大区间 。

详见： 单词拆分的遍历过程 。

3、初始化dp数组

根据dp数组的含义，我们求的是以nums[i]为结尾的最长递增子序列的长度 。

不管i是多少，其子序列至少包括nums[i]，也就是说长度至少为1 。

所以dp[i]全部初始化为1即可 。

4、确定遍历顺序

这里从左往右或者从右往左遍历其实都行 。

特别注意的一点是最后的返回值 。

通常我们都是返回dp数组的最后一个值，即dp[nums.size() - 1] 。

但这里不行 。

以题目给的示例1来说 。

示例 1:

• 输入：nums = [10,9,2,5,3,7,101,18]
• 输出：4
• 解释：最长递增子序列是 [2,3,7,101]，因此长度为 4

这里最后遍历到101（即dp[6]）时，取到最长严格递增子序列 。

显然这不是dp数组的最后一个值 。

因此我们需要设置一个变量，在循环过程中不断更新最长的子序列长度，最后返回这个最大值 。

为什么这里最长递增子序列是 [2,3,7,101] 而不可以是 [2,3,7,18]?

实际上确实也可以是后者，但我推测可能是题目中的最长"严格递增"子序列长度做出了限制 。

代码

                        
                          class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        if (nums.size() <= 1) return nums.size();
        //定义并初始化dp数组
        vector<int> dp(nums.size(), 1);
        //结果变量res
        int res  = 1;//注意，至少长度为1，因此res要初始化为1
        
        //遍历dp数组
        for(int i = 1; i < nums.size(); ++i){
            for(int j = 0; j < i; ++j){//当nums[i] > nums[j]时不断遍历[j,i]范围内的子序列
                if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
                //不满足条件就移动i扩大范围
            }
            if(dp[i] > res) res = dp[i];//更新更长的子序列长度
        }
        return res;
    }
};

                        
                      

最长连续递增序列

力扣题目链接(opens new window) 。

给定一个未经排序的整数数组，找到最长且 连续递增的子序列，并返回该序列的长度.

连续递增的子序列 可以由两个下标 l 和 r（l < r）确定，如果对于每个 l <= i < r，都有 nums[i] < nums[i + 1] ，那么子序列 [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] 就是连续递增子序列.

示例 1:

• 输入：nums = [1,3,5,4,7]
• 输出：3
• 解释：最长连续递增序列是 [1,3,5], 长度为3。尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的，因为 5 和 7 在原数组里被 4 隔开。

示例 2:

• 输入：nums = [2,2,2,2,2]
• 输出：1
• 解释：最长连续递增序列是 [2], 长度为1。

提示:

• 0 <= nums.length <= 10^4
• -10^9 <= nums[i] <= 10^9

思路

由题意，与上题最大的不同是这里要求子序列是连续的，不能跳 。

五步走

1、确定dp数组含义

dp[i]: 以下标i为结尾的连续递增的子序列长度为dp[i] 。

2、确定递推公式

根据题目的条件， 连续递增的子序列 要满足 nums[i] < nums[i + 1] 。

也就是说，如果 nums[i] > nums[i - 1]，那么以 i 为结尾的连续递增的子序列长度 一定等于 以i - 1为结尾的连续递增的子序列长度 + 1 。

所以递推公式为：dp[i] = dp[i - 1] + 1,

因为本题要求连续递增子序列，所以不用去比较nums[j]与nums[i] （j在0到i之间遍历） 。

既然不用j了，那么也不用两层for循环，本题一层for循环就行，比较nums[i] 和 nums[i - 1].

3、初始化dp数组

与上一题一样，dp[i]长度至少为1（即包含本身），因此dp数组初始化为1即可 。

4、确定遍历顺序

从递推公式看，dp[i]依赖dp[i - 1]，因此应该从前向后遍历 。

代码

                        
                          class Solution {
public:
    int findLengthOfLCIS(vector<int>& nums) {
        //处理异常
        if(nums.size() == 0) return 0;
        //定义并初始化dp数组
        vector<int> dp(nums.size(), 1);

        int res = 1;//注意，至少长度为1，因此res要初始化为1
        //遍历dp数组
        for(int i = 1; i < nums.size(); ++i){
            //子序列还满足递增趋势时执行下面的语句
            if(nums[i] > nums[i - 1]) dp[i] = dp[i - 1] + 1;   
            if(dp[i] > res) res = dp[i];
        }
        return res;
    }
};

                        
                      

最长重复子数组

力扣题目链接(opens new window) 。

给两个整数数组 A 和 B ，返回两个数组中公共的、长度最长的子数组的长度.

示例:

输入:

• A: [1,2,3,2,1]
• B: [3,2,1,4,7]
• 输出：3
• 解释：长度最长的公共子数组是 [3, 2, 1] 。

提示:

• 1 <= len(A), len(B) <= 1000
• 0 <= A[i], B[i] < 100

思路

这里要求两个数组中最长重复子数组，其实就是要在两个数组中找到最长的公共子序列 。

并且这里的子序列应该要求是连续的，也就是和 最长连续递增序列 的要求类似 。

所以我们可以仿照着去定义dp数组，但因为涉及两个数组，所以dp数组应该也要是二维的 。

五步走

1、确定dp数组含义

有两个数组nums1、nums2，那么自然需要两个指针用于遍历，分别是i、j 。

这 两个指针应该是同步移动 的，其指向的分别为：nums1和nums1中，当前子数组（子序列）的末尾 。

 。

如上图所示，指针i、j再往后移一次就不满足重复子数组的条件了，因此上述两个数组的最长重复子数组就是[1,8,3] 。

dp[i][j] ：nums1中以下标为 i - 1 和nums2中以下标为 j - 1 的最长重复子数组长度为 dp[i][j] 。

这里为什么不从i和j开始？要减1呢?

实际上是一个优化技巧，如果从i、j开始，在初始化dp数组时还要单独为 dp[i][0] 和 dp[0][j] 进行初始化，但其实这是没有必要的 。

2、确定递推公式

dp[i][j] 的状态是由 dp[i - 1][j - 1] 推导出来的 。

正确的理解思路是如下（还是拿上面的图来说） 。

我们要找的是存在于nums1、nums2中的最长公共子数组 。

当前i、j下标指向的值之前区间构成的子数组如果是nums1、nums2中公共的（相同的），那么满足条件， dp数组记录当前长度 。

i、j同时向后移动；如果不相同，dp数组不记录长度（保持为初始值），i、j仍同时向后移动 。

根据dp数组的定义， dp[i][j] 是在下标i - 1 和 j - 1时找到的最长公共子数组的状态 。

因此， dp[i][j] 的前置状态应该也要是找到对应下标下的最长公共子数组的状态，即 dp[i - 1][j - 1] ，而这两个状态在"数组长度"层面相差1，所以要用 dp[i - 1][j - 1] 推导出 dp[i][j] 就要加1 。

综上，本题的递推公式为: dp[i][j] = dp[i - 1][j - 1] + 1 。

（其实和上题的分析过程类似） 。

3、初始化dp数组

这里，因为之前在定义dp数组时，我们选择了从 i - 1 和 j - 1 开始 。

所以，根据dp数组含义， dp[i][0] 和 dp[0][j] 是没有意义的，因为我们是从 i - 1 和 j - 1 开始找（从i=1，j=1开始遍历），所以没必要初始化这俩 。

如果从i、j开始，那么 dp[i][0] 和 dp[0][j] 就是有意义的，我们需要遍历nums1、nums2来初始化（尽管可能初始化的值很怪） 。

虽然没有意义，但是肯定还是要有个初始值的，0在合适不过了 。

即， dp[i][0] = 0 、 dp[0][j] = 0 。

其他部分可以初始化为任意值（原因 详见 ），为了统一，也初始化为0 。

4、确定遍历顺序

从前向后遍历，原因说过很多次了，即i的状态需要根据i - 1推导 。

然后先遍历nums1、nums2都无所谓（长度一样） 。

代码

                        
                          class Solution {
public:
    int findLength(vector<int>& nums1, vector<int>& nums2) {
        // 创建并初始化dp数组
        // vector<vector<int>> dp(nums1.size(), vector<int>(nums2.size(), 0));//错误
        vector<vector<int>> dp(nums1.size() + 1, vector<int>(nums2.size() + 1, 0));

        int res = 0;
        //遍历dp数组
        for(int i = 1; i <= nums1.size(); ++i){//注意边界条件，小于等于
            for(int j = 1; j <= nums2.size(); ++j){//小于等于
                //为了与dp数组的定义保持一致，这里要用i - 1和j - 1为下标进行比较
                if(nums1[i - 1] == nums2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
                if(dp[i][j] > res) res = dp[i][j];
            }
        }
        return res;
    }
};

                        
                      

注意事项 TBD 。

以下代码中，为什么创建dp数组时，nums1.size() + 1 。

class Solution { 。

public

int findLength(vector & nums1, vector & nums2) { 。

​ //创建并初始化dp数组 。

​ vector<vector > dp(nums1.size() + 1, vector (nums2.size() + 1, 0)),

​ int res = 0,

​ //遍历dp数组 。

​ for(int i = 1; i <= nums1.size(); ++i){ 。

​ for(int j = 1; j <= nums2.size(); ++j){ 。

​ if(nums1[i - 1] == nums2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1,

​ if(dp[i][j] > res) res = dp[i][j],

​ } 。

​ } 。

​ return res,

} 。

},

最长公共子序列

力扣题目链接(opens new window) 。

给定两个字符串 text1 和 text2，返回这两个字符串的最长公共子序列的长度.

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串.

例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。两个字符串的「公共子序列」是这两个字符串所共同拥有的子序列.

若这两个字符串没有公共子序列，则返回 0.

示例 1

输入：text1 = "abcde", text2 = "ace" 输出：3 解释：最长公共子序列是 "ace"，它的长度为 3.

示例 2: 输入：text1 = "abc", text2 = "abc" 输出：3 解释：最长公共子序列是 "abc"，它的长度为 3.

示例 3: 输入：text1 = "abc", text2 = "def" 输出：0 解释：两个字符串没有公共子序列，返回 0.

提示

• 1 <= text1.length <= 1000
• 1 <= text2.length <= 1000 输入的字符串只含有小写英文字符

思路

与上题的区别是，这题又可以使用不连续但符合原有相对顺序的子序列了 。

开始分析 。

五步走

1、确定dp数组含义

这里要从两个字符串数组里去找公共子序列，因此仍然需要使用二维dp数组 。

dp[i][j] :下标为i - 1和j - i时，对于两个数组而言的最长公共子序列的长度为 dp[i][j] 。

（长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列为 dp[i][j] ） 。

为什么要减1？为了避免初始化 dp[i][0] 和 dp[0][j] ，详见上一题 。

2、确定递推公式

因为允许有不连续的子序列，所以这里会有多种情况 。

（1）如果当前的text1[i] == text2[j] 。

那没什么好说的，和上题的推导一模一样， dp[i][j] = dp[i - 1][j - 1] + 1 。

（2）除了相等以外的其他情况 。

这里用题目给的示例1来说明 。

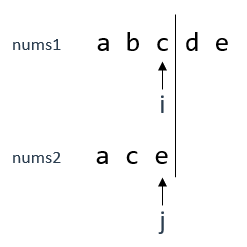
因为text2就那么长，所以遍历到黑线处就结束了，那就以这个位置举例说明（遍历到前一个位置时分析同理） 。

需要明确一下，当前情况下，我们是在[a,b,c] (text1)和[a,c,e] (text2) 中找公共子序列 。

当遍历到如上图中位置时，i指向text1的'c'，j指向text2的'e'，这两个字符显然不相等，因此无法触发情况1 。

此时有两种情况可以考虑，因为'c'和'e'已经不相等了，那就看其前面一位，看看剩下的还能不能构成公共子序列 。

情况1：text1退回一位 。

                        
                          a b c
  ↑
  i
a c e
    ↑
    j

                        
                      

现在[a,b,c] (text1)和[a,c,e] (text2) 的最长公共子序列长度是1（[a]） 。

情况2：text2退回一位 。

                        
                          a b c
    ↑
    i
a c e
  ↑
  j

                        
                      

由于可以有不连续子序列，所以[a,b,c] (text1)和[a,c,e] (text2) 的最长公共子序列长度是2（[a,c]） 。

显然，要从这两种情况中取较大的那个 。

综上，除了text1[i] == text2[j]以外的其他情况时的递推公式是： dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]),

因此，本题的递推公式完整写法如下:

                        
                          if (text1[i - 1] == text2[j - 1]) {
    dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}

                        
                      

3、初始化dp数组

首先，空串的子序列长度为0 。

然后就是text1[i - 1]和text2[j - 1]，上题说过，这俩初始化没有意义，但是还是要给个值，为了统一就给0 。

然后其他部分可任意初始化，为了统一也给0 。

4、确定遍历顺序

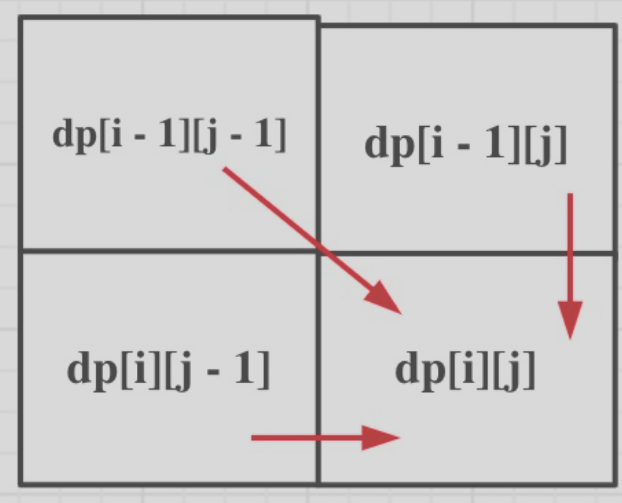
如上图所示，我们有三个方向可以推到 dp[i][j] ，因此遍历顺序应该是从前往后，从上到下 。

（详见 二维背包推导 ） 。

代码

                        
                          class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        //定义dp数组并初始化
        vector<vector<int>> dp(text1.size() + 1, vector<int>(text2.size() + 1, 0));

        int res = 0;
        //遍历dp数组
        for(int i = 1; i <= text1.size(); ++i){//注意边界条件，小于等于
            for(int j = 1; j <= text2.size(); ++j){//小于等于
                if(text1[i - 1] == text2[j - 1]){//为了与dp数组的定义保持一致，这里要用i-1和j-1为下标进行比较
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }else{
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
                }
                if(dp[i][j] > res) res = dp[i][j];
            }
        }
        return res;
    }
};

                        
                      

最后此篇关于【LeetCode动态规划#14】子序列系列题（最长递增子序列、最长连续递增序列、最长重复子数组、最长公共子序列）的文章就讲到这里了,如果你想了解更多关于【LeetCode动态规划#14】子序列系列题（最长递增子序列、最长连续递增序列、最长重复子数组、最长公共子序列）的内容请搜索CFSDN的文章或继续浏览相关文章，希望大家以后支持我的博客！ 。