- Java锁的逻辑(结合对象头和ObjectMonitor)
- 还在用饼状图?来瞧瞧这些炫酷的百分比可视化新图形(附代码实现)⛵
- 自动注册实体类到EntityFrameworkCore上下文,并适配ABP及ABPVNext
- 基于Sklearn机器学习代码实战
线性表可以用普通的一维数组存储.
你可以让线性表可以完成以下操作(代码实现很简单,这里不再赘述):
1.定义:下面有一个空链表,表头叫head,并且表内没有任何元素.
struct
node
{
int
value;
node
*
next;
} arr[MAX];
int
top=-
1
;
node
*head = NULL;
2.内存分配:在竞赛中不要用new,也不要用malloc、calloc——像下面一样做吧.
#define
NEW(p) p=&arr[++top];p->value=0;p->next=NULL
node
*
p;
NEW(head);
//
初始化表头
NEW(p);
//
新建结点
3.插入:把q插入到p的后面。时间复杂度O(1).
if
(p!=NULL && q!=NULL)
//
先判定是否为空指针。如果不是,继续。
{
q
->next=p->
next;
p
->next=
q;
}
4.删除:把p的下一元素删除。时间复杂度O(1).
if
(p!=NULL && p->next!=NULL)
//
先判定是否为空指针。如果不是,继续。
{
node
*q=p->
next;
p
->next=q->
next;
//
delete(q);
//
如果使用动态内存分配,最好将它的空间释放。
}
5.查找或遍历:时间复杂度O( n ).
node *p=
first;
while
(p!=
NULL)
{
//
处理value
//
cout<<p->value<<'\t';
p=p->
next;
}
。
指针的作用就是存储地址。如果我们找到了替代品,就可以放弃指针了.
需要把上面的定义改一下:
struct
node
{
int
value;
int
next;
//
表示下一元素在arr中的下标
} arr[MAX];
和单链表有一个重大区别:单链表最后一个元素的next指向NULL,而循环链表最后一个元素的next指向first.
遍历时要留心,不要让程序陷入死循环.
一个小技巧 :如果维护一个表尾指针last,那么就可以在O(1)的时间内查找最后一个元素。同时可以防止遍历时陷入死循环.
1.定义:下面有一个空链表,表头叫first.
struct
node
{
int
value;
node
*next, *
prev;
} arr[MAX];
int
top=-
1
;
node
*first = NULL;
//
根据实际需要可以维护一个表尾指针last。
2.内存分配:最好不要使用new运算符或malloc、calloc函数.
#define
NEW(p) p=arr+(++top);p->value=0;p->next=NULL;p->prev=NULL
node
*
p;
NEW(head);
//
初始化表头
NEW(p);
//
新建结点
3.插入:把q插入到p的后面。时间复杂度O(1).
if
(p==NULL||q==NULL)
//
先判定是否为空指针。如果不是,继续。
{
q
->prev=
p;
q
->next=p->
next;
q
->next->prev=
q;
p
->next=
q;
}
4.删除:把p的下一元素删除。时间复杂度O(1).
if
(p==NULL||p->next==NULL)
//
先判定是否为空指针。如果不是,继续。
{
node
*q=p->
next;
p
->next=q->
next;
q
->next->prev=
p;
//
delete(q);
//
如果使用动态内存分配,最好将它的空间释放。
}
5.查找或遍历:从两个方向开始都是可以的.
void
insert(
const
node *head, node *
p)
{
node
*x, *
y;
y
=
head;
do
{
x
=
y;
y
=x->
next;
}
while
((y!=NULL) && (y->value < p->
value);
x
->next=
p;
p
->next=
y;
}
操作规则 :先进后出,先出后进.
int stack[ N ], top=0; // top 表示栈顶位置.
入栈 : inline void push(int a) { stack[top++]=a; } 。
出栈 : inline int pop() { return stack[--top],
栈空的条件 : inline bool empty() { return top<0; } 。
如果两个栈有相反的需求,可以用这种方法节省空间:用一个数组表示两个栈。分别用 top1 、 top2 表示栈顶的位置,令 top1 从 0 开始, top2 从 N -1 开始.
。
。
递归其实也用到了栈。每调用一次函数,都相当于入栈( 当然这步操作 “隐藏在幕后” )。函数调用完成,相当于出栈.
。
一般情况下,调用栈的空间大小为 16MB 。也就是说,如果递归次数太多,很容易因为栈溢出导致程序崩溃,即“爆栈”.
。
为了防止 “爆栈”,可以将递归用栈显式实现。如果可行,也可以改成迭代、递推等方法.
。
使用栈模拟递归时,注意入栈的顺序 ——逆序入栈,后递归的要先入栈,先递归的要后入栈.
。
下面是非递归版本的 DFS 模板:
。
stack <
int
> s;
//
存储状态
void
DFS(
int
v, …)
{
s.push(v);
//
初始状态入栈
while
(!
s.empty())
{
int
x = s.top(); s.pop();
//
获取状态
//
处理结点
if
(x达到某种条件)
{
//
输出、解的数量加1、更新目前搜索到的最优值等
…
return
;
}
//
寻找下一状态。当然,不是所有的搜索都要这样寻找状态。
//
注意,这里寻找状态的顺序要与递归版本的顺序相反,即逆序入栈。
for
(i=n-
1
;i>=
0
;i--
)
{
s.push(…
/*
i对应的状态
*/
);
}
}
//
无解
cout<<
"
No Solution.
"
;
}
。
。
。
。
。
操作规则 :先进先出,后进后出.
定义: int queue[N], front=0, rear=0,
front指向队列首个元素,rear指向队列尾部元素的右侧.
入队 :inline void push(int a) { queue[rear++]=a; } 。
出队 :inline int pop() { return queue[front++]; } 。
队空的条件 :inline bool empty() { return front==rear; } 。
循环队列——把链状的队列变成了一个环状队列。与上面的链状队列相比,可以节省很大空间.
定义 :int queue[N], front=0, rear=0; front指向队列首个元素,rear指向队列尾部元素的右侧.
入队 :inline void push(int a) { queue[rear]=a; rear=(rear+1)%N; } 。
出队 :inline int pop() { int t=queue[front]; front=(front+1)%N; return t; } 。
队满或队空的条件 :inline bool empty() { return front==rear; } 队满和队空都符合上述条件。怎么把它们区分开呢? 第一种方法:令队列的大小是 N +1,然后只使用 N 个元素。这样队满和队空的条件就不一样了。 第二种方法:在入队和出队同时记录队列元素个数。这样,直接检查元素个数就能知道队列是空还是满.
BFS要借助队列来完成,并且,将队列改成堆栈,BFS就变成了DFS。BFS的具体实现见42页“3.7 代码模板”.
struct
node
{
int
value;
node
*leftchild, *
rightchild;
//
int id;
//
结点编号。
//
node *parent;
//
指向父亲结点。
} arr[N];
int
top=-
1
;
node
* head =
NULL;
#define
NEW(p) p=&arr[++top]; p->leftchild=NULL; \
p
->rightchild=NULL; p->value=
0
。
。
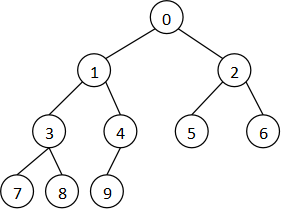
。
。
。
如果一个二叉树的结点严格按照从上到下、从左到右的顺序填充,就可以用一个一维数组保存.
下面假设这个树有 n 个结点,待操作的结点是 r (0≤ r < n ).
| 操作 。 |
宏定义 。 |
r 的取值范围 。 |
| r的父亲 。 |
#define parent(r) (((r)-1)/2) 。 |
r ≠0 。 |
| r的左儿子 。 |
#define leftchild(r) ((r)*2+1) 。 |
2 r +1< n 。 |
| r的右儿子 。 |
#define rightchild(r) ((r)*2+2) 。 |
2 r +2< n 。 |
| r的左兄弟 。 |
#define leftsibling(r) ((r)-1) 。 |
r 为偶数且0< r ≤ n -1 。 |
| r的右兄弟 。 |
#define rightsibling(r) ((r)+1) 。 |
r 为奇数且 r +1< n 。 |
| 判断r是否为叶子 。 |
#define isleaf(r) ((r)>=n/2) 。 |
r < n 。 |
。
1. 前序遍历 。
。
void
preorder(node *
p)
{
if
(p==NULL)
return
;
//
处理结点p
cout<<p->value<<
'
'
;
preorder(p
->
leftchild);
preorder(p
->
rightchild);
}
。
2. 中序遍历 。
void
inorder(node *
p)
{
if
(p==NULL)
return
;
inorder(p
->
leftchild);
//
处理结点p
cout<<p->value<<
'
'
;
inorder(p
->
rightchild);
}
3. 后序遍历 。
。
void
postorder(node *
p)
{
if
(p==NULL)
return
;
postorder(p
->
leftchild);
postorder(p
->
rightchild);
//
处理结点p
cout<<p->value<<
'
'
;
}
。
假如二叉树是通过动态内存分配建立起来的,在释放内存空间时应该使用后序遍历.
。
4. 宽度优先遍历( BFS ) 。
。
首先访问根结点,然后逐个访问第一层的结点,接下来逐个访问第二层的结点 …… 。
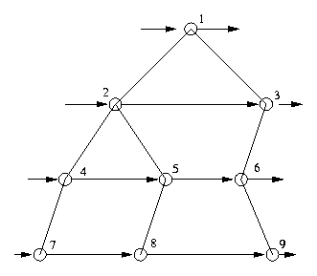
。
。
node *
q[N];
void
BFS(node *
p)
{
if
(p==NULL)
return
;
int
front=
1
,rear=
2
;
q[
1
]=
p;
while
(front<
rear)
{
node
*t = q[front++
];
//
处理结点t
cout<<t->value<<
'
'
;
if
(t->leftchild!=NULL) q[rear++]=t->
leftchild;
if
(t->rightchild!=NULL) q[rear++]=t->
rightchild;
}
}
对于完全二叉树,可以直接遍历:
for
(
int
i=
0
; i<n; i++) cout<<a[i]<<
'
'
;
。
【问题描述】二叉树的遍历方式有三种:前序遍历、中序遍历和后序遍历。现在给出其中两种遍历的结果,请输出第三种遍历的结果.
。
。
。
【分析】 。
。
前序遍历的第一个元素是根,后序遍历的最后一个元素也是根。所以处理时需要到中序遍历中找根,然后递归求出树.
。
注意!输出之前须保证字符串的最后一个字符是 '\0' .
。
1. 中序+后序→前序 。
void
preorder(
int
n,
char
*pre,
char
*
in
,
char
*
post)
{
if
(n<=
0
)
return
;
int
p=strchr(
in
, post[n-
1
])-
in
;
pre[
0
]=post[n-
1
];
preorder(p, pre
+
1
,
in
, post);
preorder(n
-p-
1
, pre+p+
1
,
in
+p+
1
, post+
p);
}
2. 前序 + 中序 → 后序 。
。
void
postorder(
int
n,
char
*pre,
char
*
in
,
char
*
post)
{
if
(n<=
0
)
return
;
int
p=strchr(
in
, pre[
0
])-
in
;
postorder(p, pre
+
1
,
in
, post);
postorder(n
-p-
1
, pre+p+
1
,
in
+p+
1
, post+
p);
post[n
-
1
]=pre[
0
];
}
。
3. 前序+后序→中序 。
“中+前”和“中+后”都能产生唯一解,但是“前+后”有多组解。下面输出其中一种.
bool
check(
int
n,
char
*pre,
char
*post)
//
判断pre、post是否属于同一棵二叉树
{
bool
b;
for
(
int
i=
0
; i<n; i++
)
{
b
=
false
;
for
(
int
j=
0
; j<n; j++
)
if
(pre[i]==
post[j])
{
b
=
true
;
break
;
}
if
(!b)
return
false
;
}
return
true
;
}
void
inorder(
int
n,
char
*pre,
char
*
in
,
char
*
post)
{
if
(n<=
0
)
return
;
int
p=
1
;
while
(check(p, pre+
1
, post)==
false
&& p<
n)
p
++
;
if
(p>=n) p=n-
1
;
//
此时,如果再往inorder里传p,pre已经不含有效字符了。
inorder(p, pre+
1
,
in
, post);
in
[p]=pre[
0
];
inorder(n
-p-
1
, pre+p+
1
,
in
+p+
1
, post+
p);
}
从任意一点出发,搜索距离它最远的点,则这个最远点必定在树的直径上。再搜索这个最远点的最远点,这两个最远点的距离即为二叉树的直径.
求树、图(连通图)的直径的思想是相同的.
。
//
结点编号从1开始,共n个结点。
struct
node
{
int
v;
node
*parent, *leftchild, *
rightchild;
} a[
1001
], *
p;
int
maxd;
bool
T[
1003
];
#define
t(x) T[((x)==NULL)?0:((x)-a+1)]
node
*
p;
void
DFS(node * x,
int
l)
{
if
(l>maxd) maxd=l, p=
x;
if
(x==NULL)
return
;
t(x)
=
false
;
if
(t(x->parent)) DFS(x->parent, l+
1
);
if
(t(x->leftchild)) DFS(x->leftchild, l+
1
);
if
(t(x->rightchild)) DFS(x->rightchild, l+
1
);
}
int
distance(node *tree)
//
tree已经事先读好
{
maxd
=
0
;
memset(T,
0
,
sizeof
(T));
for
(
int
i=
1
; i<=n; i++
)
T[i]
=
true
;
DFS(tree,
0
);
maxd
=
0
;
memset(T,
0
,
sizeof
(T));
for
(
int
i=
1
; i<=n; i++) T[i]=
true
;
DFS(p,
0
);
return
maxd;
}
。
并查集最擅长做的事情——将两个元素合并到同一集合、判断两个元素是否在同一集合中.
并查集用到了树的父结点表示法。在并查集中,每个元素都保存自己的父亲结点的编号,如果自己就是根结点,那么父亲结点就是自己。这样就可以用树形结构把在同一集合的点连接到一起了.
struct
node
{
int
parent;
//
表示父亲结点。当编号i==parent时为根结点。
int
count;
//
当且仅当为根结点时有意义:表示自己及子树元素的个数
int
value;
//
结点的值
}
set
[N];
int
Find(
int
x)
//
查找算法的递归版本(建议不用这个)
{
return
(
set
[x].parent==x) ? x : (
set
[x].parent = Find(
set
[x].parent));
}
int
Find(
int
x)
//
查找算法的非递归版本
{
int
y=
x;
while
(
set
[y].parent != y)
//
寻找父亲结点
y =
set
[y].parent;
while
(x!=y)
//
路径压缩,即把途中经过的结点的父亲全部改成y。
{
int
temp =
set
[x].parent;
set
[x].parent =
y;
x
=
temp;
}
return
y;
}
void
Union(
int
x,
int
y)
//
小写的union是关键字。
{
x
=Find(x); y=Find(y);
//
寻找各自的根结点
if
(x==y)
return
;
//
如果不在同一个集合,合并
if
(
set
[x].count >
set
[y].count)
//
启发式合并,使树的高度尽量小一些
{
set
[y].parent =
x;
set
[x].count +=
set
[y].count;
}
else
{
set
[x].parent =
y;
set
[y].count +=
set
[x].count;
}
}
void
Init(
int
cnt)
//
初始化并查集,cnt是元素个数
{
for
(
int
i=
1
; i<=cnt; i++
)
{
set
[i].parent=
i;
set
[i].count=
1
;
set
[i].value=
0
;
}
}
void
compress(
int
cnt)
//
合并结束,再进行一次路径压缩
{
for
(
int
i=
1
; i<=cnt; i++
) Find(i);
}
说明 :
使用之前调用Init()! 。
Union(x,y):把 x 和 y 进行启发式合并,即让节点数比较多的那棵树作为“树根”,以降低层次.
Find(x):寻找 x 所在树的根结点。Find的时候,顺便进行了路径压缩。 上面的Find有两个版本,一个是递归的,另一个是非递归的.
判断 x 和 y 是否在同一集合:if (Find(x)==Find(y)) …… 。
在所有的合并操作结束后,应该执行compress().
并查集的效率很高,执行 m 次查找的时间约为O(5 m ).
数据结构是计算机科学的重要分支。选择合适的数据结构,可以简化问题,减少时间的浪费.
线性表有两种存储方式,一种是顺序存储,另一种是链式存储。前者只需用一维数组实现,而后者既可以用数组实现,又可以用指针实现.
顺序表的特点是占用空间较小,查找和定位的速度很快,但是插入和删除元素的速度很慢(在尾部速度快);链表和顺序表正好相反,它的元素插入和删除速度很快,但是查找和定位的速度很慢(同样,在首尾速度快).
。
栈和队列以线性表为基础。它们的共同点是添加、删除元素都有固定顺序,不同点是删除元素的顺序。队列从表头删除元素,而栈从表尾删除元素,所以说队列是先进先出表,堆栈是先进后出表.
栈和队列在搜索中有非常重要的应用。栈可以用来模拟深度优先搜索,而广度优先搜索必须用队列实现.
有时为了节省空间,栈的两头都会被利用,而队列会被改造成循环队列.
。
上面几种数据结构都是线性结构。而二叉树是一种很有用的非线性结构。二叉树可以采用以下的递归定义:二叉树要么为空,要么由根结点、左子树和右子树组成。左子树和右子树分别是一棵二叉树.
计算机中的树和现实生活不同——计算机里的树是倒置的,根在上,叶子在下.
完全二叉树:一个完全二叉树的结点是从上到下、从左到右地填充的。如果高度为 h ,那么0~ h -1层一定已经填满,而第 h 层一定是从左到右连续填充的.
通常情况下,二叉树用指针实现。对于完全二叉树,可以用一维数组实现(事先从0开始编号).
访问二叉树的所有结点的过程叫做二叉树的遍历。常用的遍历方式有前序遍历、中序遍历、后序遍历,它们都是递归完成的.
。
树也可以采用递归定义:树要么为空,要么由根结点和 n ( n ≥0)棵子树组成.
森林由 m ( m ≥0)棵树组成.
二叉树不是树的一种,因为二叉树的子树中有严格的左右之分,而树没有。这样,树可以用父结点表示法来表示(当然,森林也可以)。并查集的合并、查询速度很快,它就是用父结点表示法实现的.
不过父结点表示法的遍历比较困难,所以常用“左儿子右兄弟”表示法把树转化成二叉树.
树的遍历和二叉树的遍历类似,不过不用中序遍历。它们都是递归结构,所以可以在上面实施动态规划.
树作为一种特殊的图,在图论中也有广泛应用.
。
树的表示方法有很多种.
第一种是父节点表示法,它适合并查算法,但不便遍历.
第二种是子节点表表示法.
。
。
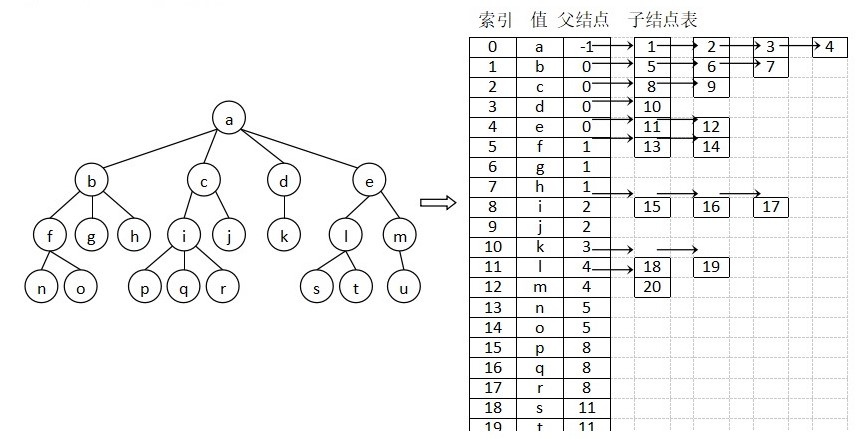
。
第三种是“左儿子右兄弟”表示法.
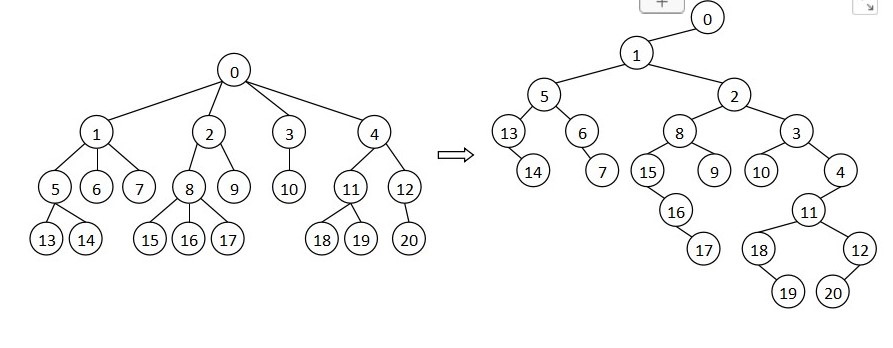
。
。
。
最后此篇关于c++基本数据结构的文章就讲到这里了,如果你想了解更多关于c++基本数据结构的内容请搜索CFSDN的文章或继续浏览相关文章,希望大家以后支持我的博客! 。
我目前正在尝试基于哈希表构建字典。逻辑是:有一个名为 HashTable 的结构,其中包含以下内容: HashFunc HashFunc; PrintFunc PrintEntry; CompareF
如果我有一个指向结构/对象的指针,并且该结构/对象包含另外两个指向其他对象的指针,并且我想删除“包含这两个指针的对象而不破坏它所持有的指针”——我该怎么做这样做吗? 指向对象 A 的指针(包含指向对象
像这样的代码 package main import "fmt" type Hello struct { ID int Raw string } type World []*Hell
我有一个采用以下格式的 CSV: Module, Topic, Sub-topic 它需要能够导入到具有以下格式的 MySQL 数据库中: CREATE TABLE `modules` ( `id
通常我使用类似的东西 copy((uint8_t*)&POD, (uint8_t*)(&POD + 1 ), back_inserter(rawData)); copy((uint8_t*)&PODV
错误 : 联合只能在具有兼容列类型的表上执行。 结构(层:字符串,skyward_number:字符串,skyward_points:字符串)<> 结构(skyward_number:字符串,层:字符
我有一个指向结构的指针数组,我正在尝试使用它们进行 while 循环。我对如何准确初始化它并不完全有信心,但我一直这样做: Entry *newEntry = malloc(sizeof(Entry)
我正在学习 C,我的问题可能很愚蠢,但我很困惑。在这样的函数中: int afunction(somevariables) { if (someconditions)
我现在正在做一项编程作业,我并没有真正完全掌握链接,因为我们还没有涉及它。但是我觉得我需要它来做我想做的事情,因为数组还不够 我创建了一个结构,如下 struct node { float coef;
给定以下代码片段: #include #include #define MAX_SIZE 15 typedef struct{ int touchdowns; int intercepti
struct contact list[3]; int checknullarray() { for(int x=0;x<10;x++) { if(strlen(con
这个问题在这里已经有了答案: 关闭 11 年前。 Possible Duplicate: Empty “for” loop in Facebook ajax what does AJAX call
我刚刚在反射器中浏览了一个文件,并在结构构造函数中看到了这个: this = new Binder.SyntaxNodeOrToken(); 我以前从未见过该术语。有人能解释一下这个赋值在 C# 中的
我经常使用字符串常量,例如: DICT_KEY1 = 'DICT_KEY1' DICT_KEY2 = 'DICT_KEY2' ... 很多时候我不介意实际的文字是什么,只要它们是独一无二的并且对人类读
我是 C 的新手,我不明白为什么下面的代码不起作用: typedef struct{ uint8_t a; uint8_t* b; } test_struct; test_struct
您能否制作一个行为类似于内置类之一的结构,您可以在其中直接分配值而无需调用属性? 前任: RoundedDouble count; count = 5; 而不是使用 RoundedDouble cou
这是我的代码: #include typedef struct { const char *description; float value; int age; } swag
在创建嵌套列表时,我认为 R 具有对列表元素有用的命名结构。我有一个列表列表,并希望应用包含在任何列表中的每个向量的函数。 lapply这样做但随后剥离了列表的命名结构。我该怎么办 lapply嵌套列
我正在做一个用于学习目的的个人组织者,我从来没有使用过 XML,所以我不确定我的解决方案是否是最好的。这是我附带的 XML 文件的基本结构:
我是新来的 nosql概念,所以当我开始学习时 PouchDB ,我找到了这个转换表。我的困惑是,如何PouchDB如果可以说我有多个表,是否意味着我需要创建多个数据库?因为根据我在 pouchdb

我是一名优秀的程序员,十分优秀!