本文已收录到 AndroidFamily ，技术和职场问题，请关注公众号 [彭旭锐] 提问.

大家好，我是小彭.

上周末是 LeetCode 第 339 场周赛，你参加了吗？这场周赛覆盖的知识点比较少，前三题很简单，第四题上难度.

---

周赛大纲

2609. 最长平衡子字符串（Easy） 。

• 模拟：$O(n)$

2610. 转换二维数组（Medium） 。

• 贪心：$O(n)$

2611. 老鼠和奶酪（Medium） 。

• 排序 + 贪心：$O(nlgn)$

2612. 最少翻转操作数（Hard） 。

• 题解一：拓扑排序 · 超出时间限制 $O(nk)$
• 题解二：BFS + 平衡二叉树 $O(nlgn)$

---

2609. 最长平衡子字符串（Easy）

题目地址

https://leetcode.cn/problems/find-the-longest-balanced-substring-of-a-binary-string/ 。

题目描述

给你一个仅由  0  和  1  组成的二进制字符串  s  .

如果子字符串中  所有的   0   都在   1   之前  且其中  0  的数量等于  1  的数量，则认为  s  的这个子字符串是平衡子字符串。请注意，空子字符串也视作平衡子字符串.

返回   s  中最长的平衡子字符串长度.

子字符串是字符串中的一个连续字符序列.

题解（模拟）

简单模拟题.

维护连续 0 的计数 cnt0 和连续 1 的计数 cnt1 ，并在 cnt0 == cnt1 时更新最长平衡子串长度为 2 * cnt1 。另外，在每段 0 的起始位置重新计数.

                        
                          class Solution {
    fun findTheLongestBalancedSubstring(s: String): Int {
        var index = 0
        var cnt0 = 0
        var cnt1 = 0
        var ret = 0
        while (index < s.length) {
            if (s[index] == '0') {
                // 每段 0 的起始位置清零
                if (index > 0 && s[index - 1] == '1') {
                    cnt0 = 0
                    cnt1 = 0
                }
                cnt0++
            } else {
                cnt1++
            }
            if (cnt1 <= cnt0) ret = Math.max(ret, cnt1 * 2)
            index++
        }
        return ret
    }
}

                        
                      

复杂度分析:

• 时间复杂度：$O(n)$ 其中 $n$ 为 $nums$ 数组的长度；
• 空间复杂度：$O(1)$ 仅使用常数级别变量。

---

2610. 转换二维数组（Medium）

题目地址

https://leetcode.cn/problems/convert-an-array-into-a-2d-array-with-conditions/ 。

题目描述

给你一个整数数组  nums  。请你创建一个满足以下条件的二维数组:

• 二维数组应该  只  包含数组  nums  中的元素。
• 二维数组中的每一行都包含  不同  的整数。
• 二维数组的行数应尽可能  少  。

返回结果数组。如果存在多种答案，则返回其中任何一种.

请注意，二维数组的每一行上可以存在不同数量的元素.

题解（贪心）

贪心思路：首先计算每个元素的出现次数，为了避免同一行的重复，将重复元素从上到下排列到不同行中.

优化：可以在一次遍历中完成，在出现更大出现次数时增加一行，在更新元素技术 cnt 后插入到第 cnt - 1 行.

                        
                          class Solution {
    fun findMatrix(nums: IntArray): List<List<Int>> {
        val cnts = IntArray(201)
        val ret = LinkedList<LinkedList<Int>>()
        var maxCnt = 0
        // 计数
        for (num in nums) {
            // 累加
            val curCnt = ++cnts[num]
            // 创建新行
            if (curCnt > maxCnt) {
                maxCnt = curCnt
                ret.add(LinkedList<Int>())
            }
            // 分布
            ret[curCnt - 1].add(num)
        }
        return ret
    }
}

                        
                      

复杂度分析:

• 时间复杂度：$O(n)$ 其中 $n$ 为 $nums$ 数组的长度，每个元素访问一次；
• 空间复杂度：$O(U)$ 计数数组空间。

---

2611. 老鼠和奶酪（Medium）

题目地址

https://leetcode.cn/problems/mice-and-cheese/ 。

题目描述

有两只老鼠和  n  块不同类型的奶酪，每块奶酪都只能被其中一只老鼠吃掉.

下标为  i  处的奶酪被吃掉的得分为:

• 如果第一只老鼠吃掉，则得分为  reward1[i]  。
• 如果第二只老鼠吃掉，则得分为  reward2[i]  。

给你一个正整数数组  reward1  ，一个正整数数组  reward2  ，和一个非负整数  k  .

请你返回第一只老鼠恰好吃掉  k  块奶酪的情况下， 最大  得分为多少.

题解（排序 + 贪心）

容易理解：为了使最终得分最大，应该让每只老鼠吃到尽可能大的奶酪.

由于两只老鼠吃的奶酪是互斥关系，因此我们可以先假设所有奶酪被第一只老鼠食得，然后再挑选 n - k 个奶酪还给第二只老鼠.

那么，对于每个位置 i ，将奶酪从第一只老鼠还给第二只老鼠存在差值 diff = reward2[i] - reward1[i] ，表示得分的差值为 diff 。差值为正得分变大，差值为负得分降低，显然降低越少越好.

因此，我们的算法是对 diff 排序，将得分降低越大的位置保留给第一只老鼠，其他还给第二只老鼠.

                        
                          class Solution {
    fun miceAndCheese(reward1: IntArray, reward2: IntArray, k: Int): Int {
        // 贪心：优先选择差值最大的位置
        val n = reward1.size
        var ret = 0
        val indexs = Array(n) { it }
        // 升序
        Arrays.sort(indexs) { i1, i2 ->
            (reward2[i1] - reward1[i1]) - (reward2[i2] - reward1[i2])
        }
        for (i in 0 until n) {
            ret += if (i < k) {
                reward1[indexs[i]]
            } else {
                reward2[indexs[i]]
            }
        }
        return ret
    }
}

                        
                      

复杂度分析:

• 时间复杂度：$O(nlgn + n)$ 其中 $n$ 为 $nums$ 数组的长度；
• 空间复杂度：$O(n + lgn)$ 索引数组和递归栈空间。

---

2612. 最少翻转操作数（Hard）

题目地址

https://leetcode.cn/problems/minimum-reverse-operations/ 。

题目描述

给你一个整数  n  和一个在范围  [0, n - 1]  以内的整数  p  ，它们表示一个长度为  n  且下标从  0  开始的数组  arr  ，数组中除了下标为  p  处是  1  以外，其他所有数都是  0  .

同时给你一个整数数组  banned  ，它包含数组中的一些位置。 banned  中第  i  个位置表示  arr[banned[i]] = 0  ，题目保证  banned[i] != p  .

你可以对  arr  进行  若干次  操作。一次操作中，你选择大小为  k  的一个  子数组  ，并将它  翻转  。在任何一次翻转操作后，你都需要确保  arr  中唯一的  1  不会到达任何  banned  中的位置。换句话说， arr[banned[i]]  始终  保持   0  .

请你返回一个数组  ans  ，对于 ** [0, n - 1]  之间的任意下标  i  ， ans[i]  是将  1  放到位置  i  处的  最少  翻转操作次数，如果无法放到位置  i  处，此数为  -1  .

• 子数组  指的是一个数组里一段连续  非空  的元素序列。
• 对于所有的  i  ， ans[i]  相互之间独立计算。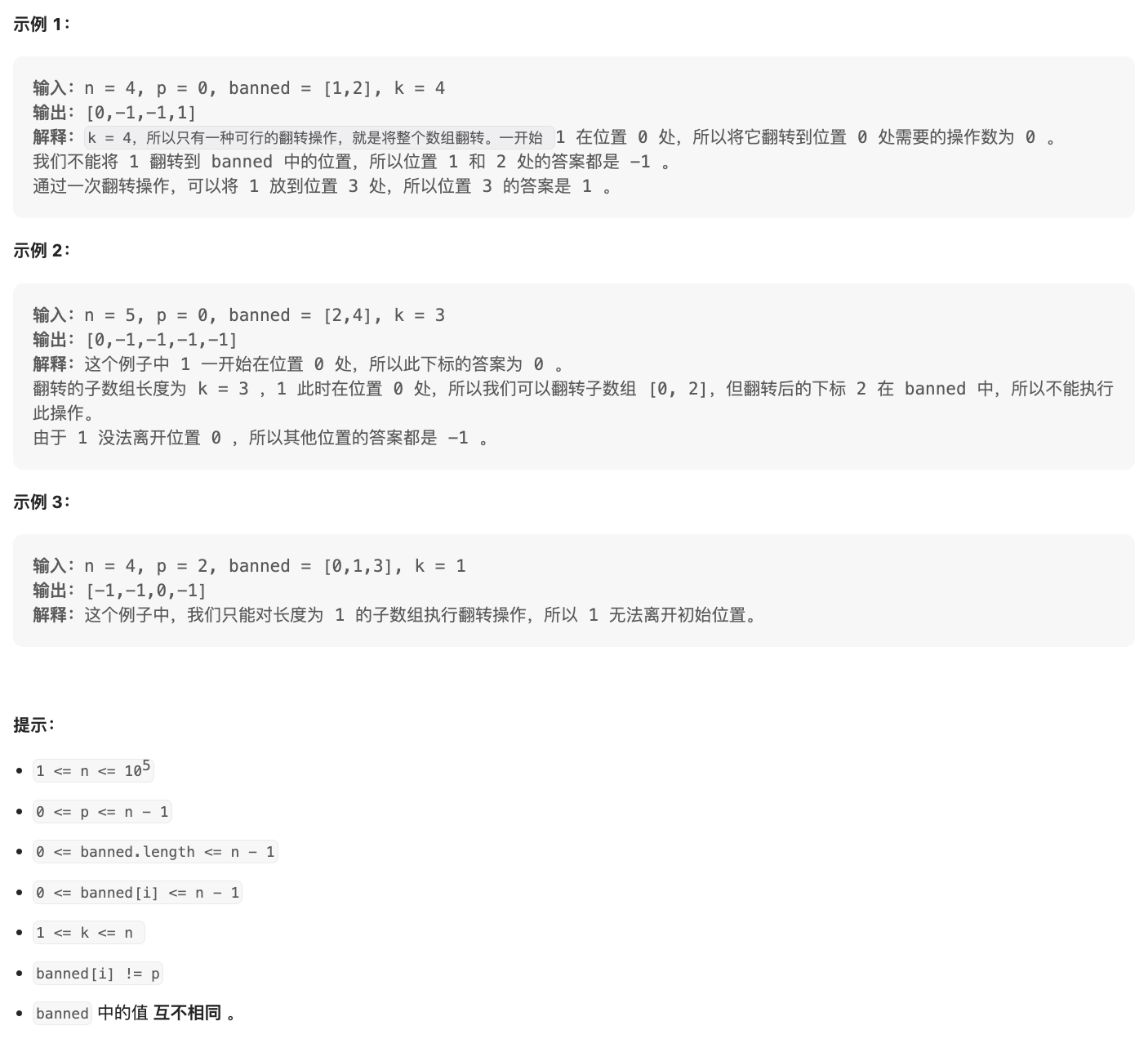
• 将一个数组中的元素  翻转  指的是将数组中的值变成  相反顺序  。

题解一（拓扑排序 · 超出时间限制）

分析 1：对于翻转窗口 [L, R] 中的位置 i，翻转后的下标为 $\frac{L+R}{2} + （\frac{L+R}{2} - i) = L + R - i$ 。

分析 2：首先位置 p 的翻转次数恒等于 0，而 banned 数组表示的位置翻转次数恒等于 -1.

分析 3：当位置 i 位于翻转窗口的左半部分时，将翻转到更大位置；当位置 i 位于翻转窗口的右半部分时，将翻转到更小位置； 。

分析 4：现在我们需要分析位置 i （初始 i 为 0 ）可以翻转到的位置:

• 情况 1：如果将 i 作为翻转窗口的左右边界，则有：
  • 位于左边界时，翻转后的下标为 i + k - 1 ；
  • 位于有边界时，翻转后的下标为 i - k + 1 。
• 情况 2：如果将 i 放在翻转窗口内部，则所有翻转后的下标正好构成差值为 2 的等差数列。

因此，i 可以翻转的区间为 [i - k + 1, i + k - 1] 中间隔 2 的位置（排除 banned 数组），或者理解为奇偶性相同的下标.

分析 5：由于翻转窗口有位置限制，会限制翻转:

• 窗口左边界在位置 0 时，且 i 位于翻转窗口的右半部分时（准备向左翻），则翻转后的位置是 0 + (k - 1) - i = k - 1 - i 。由于窗口无法继续左移，所以小于 k - i - 1 的位置都不可达；
• 同理，窗口右边界位于 n - 1 时，且 i 位于翻转窗口的左边部分时（准备向右翻），则翻转后的位置是 (n - k) + (n - 1) - i = 2n - k - i - 1 。由于窗口无法继续右移，所以大于 2n - k - i - 1 的位置都不可达。

综上，可得翻转后区间为 [max(i - k + 1, k - i - 1), min(i + k - 1, 2n - k - i - 1)] 中与 i 奇偶性相同的位置.

至此，容易发现问题可以用拓扑排序（BFS 写法）解决：初始时将 p 位置入队，随后每一轮的翻转次数 + 1，并将该位置入队.

                        
                          class Solution {
    fun minReverseOperations(n: Int, p: Int, banned: IntArray, k: Int): IntArray {
        val ret = IntArray(n) { -1 }
        // 初始位
        ret[p] = 0
        // 禁止位
        val bannedSet = banned.toHashSet()
        // BFS（最小跳转索引）
        val queue = LinkedList<Int>()
        queue.offer(p)
        while (!queue.isEmpty()) {
            val i = queue.poll()!!
            val min = Math.max(i - k + 1, k - i - 1)
            val max = Math.min(i + k - 1, 2 * n - k - i - 1)
            val curStep = ret[i] + 1
            for (j in min..max step 2) {
                // 不可达
                if (bannedSet.contains(j)) continue
                // 已访问
                if (ret[j] != -1) continue
                // 可达
                ret[j] = curStep
                // 入队
                queue.offer(j)
            }
        }
        return ret
    }
}

                        
                      

复杂度分析:

• 时间复杂度：$O(n·k)$ 每个元素最多访问 1 次，且每轮最多需要访问 $k$ 个元素。
• 空间复杂度：$O(n)$ 队列的长度最大为 $n$。

题解二（BFS + 平衡二叉树）

在题解一中，当 k 比较大时每轮 BFS 中会重复判断已经被标记过的位置，如何避免呢？我们可以提前将所有下标加入到散列表中，在每次标记后将下标从散列表移除，这样能避免重复访问已经标记过的位置.

其次，由于每轮中需要标记的区间位于 [min, max] ，那么我们可以将散列表升级为基于平衡二叉树的 TreeSet，以便在 O(lgn) 时间内找到区间中的元素。具体方式是寻找树中大于等于 min 的最小元素（且小于等于 max ），将其标记和移除.

最后，由于偶数下标和奇数下标是分开的，所以需要建立两个平衡二叉树.

                        
                          class Solution {
    fun minReverseOperations(n: Int, p: Int, banned: IntArray, k: Int): IntArray {
        val ret = IntArray(n) { -1 }
        // 初始位
        ret[p] = 0
        // 禁止位
        val bannedSet = banned.toHashSet()
        // 平衡二叉树
        val sets = Array(2) { TreeSet<Int>() }
        for (i in 0 until n) {
            if (i != p && !bannedSet.contains(i)) sets[i % 2].add(i)
        }
        // BFS（最小跳转索引）
        val queue = LinkedList<Int>()
        queue.offer(p)
        while (!queue.isEmpty()) {
            val i = queue.poll()!!
            val min = Math.max(i - k + 1, k - i - 1)
            val max = Math.min(i + k - 1, 2 * n - k - i - 1)
            val curStep = ret[i] + 1
            // 根据左端点确定奇偶性（右端点也行）
            val set = sets[min % 2]
            // 枚举平衡树中的 [min,max] 区间
            while (true) {
                val index = set.ceiling(min) ?: break // 大于等于 min 的最小键值
                if (index > max) break
                // 标记并删除
                set.remove(index)
                ret[index] = curStep
                // 入队
                queue.offer(index)
            }
        }
        return ret
    }
}

                        
                      

复杂度分析:

• 时间复杂度：$O(nlgn + nlgn)$ 建平衡树为 $O(nlgn)$，BFS 中每个元素最多删除一次，每轮需要 $O(lgn)$ 时间找到左边界，整体是 $O(nlgn)$；
• 空间复杂度：$O(n)$ 平衡二叉树空间。

---

点击上方按钮关注 每周持续原创更新 与你一起深度思考 。

The End 。

—— 我 们 下 次 见 —— 。

最后此篇关于刷爆LeetCode周赛339，贪心/排序/拓扑排序/平衡二叉树的文章就讲到这里了,如果你想了解更多关于刷爆LeetCode周赛339，贪心/排序/拓扑排序/平衡二叉树的内容请搜索CFSDN的文章或继续浏览相关文章，希望大家以后支持我的博客！ 。