Ceres 自动求导解析-从原理到实践

1.0 前言

Ceres 有一个自动求导功能，只要你按照Ceres要求的格式写好目标函数，Ceres会自动帮你计算 精确 的导数（或者雅克比矩阵），这极大节约了算法开发者的时间，但是笔者在使用的时候一直觉得这是个黑盒子，特别是之前在做深度学习的时候，神经网络本事是一个很盒模型了，再加上 pytorch 的自动求导，简直是黑上加黑。现在转入视觉SLAM方向，又碰到了 Ceres 的自动求导，是时候揭开其真实的面纱了。知其然并知其所以然才是一名算法工程师应有的基本素养.

2.0 Ceres求导简介

Ceres 一共有三种求导的方式提供给开发者，分别是:

• 解析求导，也就是手动计算出导数的解析形式.

  例如有如下函数,

  \[y = \frac{b_1}{(1+e^{b_2-b_3x})^{1/b_4}} \]

  构建误差函数:

  \[\begin{split}\begin{align} E(b_1, b_2, b_3, b_4) &= \sum_i f^2(b_1, b_2, b_3, b_4 ; x_i, y_i)\\ &= \sum_i \left(\frac{b_1}{(1+e^{b_2-b_3x_i})^{1/b_4}} - y_i\right)^2\\ \end{align}\end{split} \]

  对待优化变量的导数为:

  \[\begin{split}\begin{align} D_1 f(b_1, b_2, b_3, b_4; x,y) &= \frac{1}{(1+e^{b_2-b_3x})^{1/b_4}}\\ D_2 f(b_1, b_2, b_3, b_4; x,y) &= \frac{-b_1e^{b_2-b_3x}}{b_4(1+e^{b_2-b_3x})^{1/b_4 + 1}} \\ D_3 f(b_1, b_2, b_3, b_4; x,y) &= \frac{b_1xe^{b_2-b_3x}}{b_4(1+e^{b_2-b_3x})^{1/b_4 + 1}} \\ D_4 f(b_1, b_2, b_3, b_4; x,y) & = \frac{b_1 \log\left(1+e^{b_2-b_3x}\right) }{b_4^2(1+e^{b_2-b_3x})^{1/b_4}} \end{align}\end{split} \]

• 数值求导，当对变量增加一个微小的增量，然后观察此时的残差和原先残差的下降比例即可，其实就是导数的定义.

  \[Df(x) = \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} \]

  当然其实也有两种形式对导数进行数值上的近似，第一种是Forward Differences:

  \[Df(x) \approx \frac{f(x + h) - f(x)}{h} \]

  第二种是 Central Differences:

  \[Df(x) \approx \frac{f(x + h) - f(x - h)}{2h} \]

  Ceres 的官方文档上是认为第二种比第一种好的，但是其实官方还介绍了第三种，这里就不详说了，感兴趣的可以去看官方文档： Ridders’ Method .

  这里有三种数值微分方法的效果对比，从右向左看:

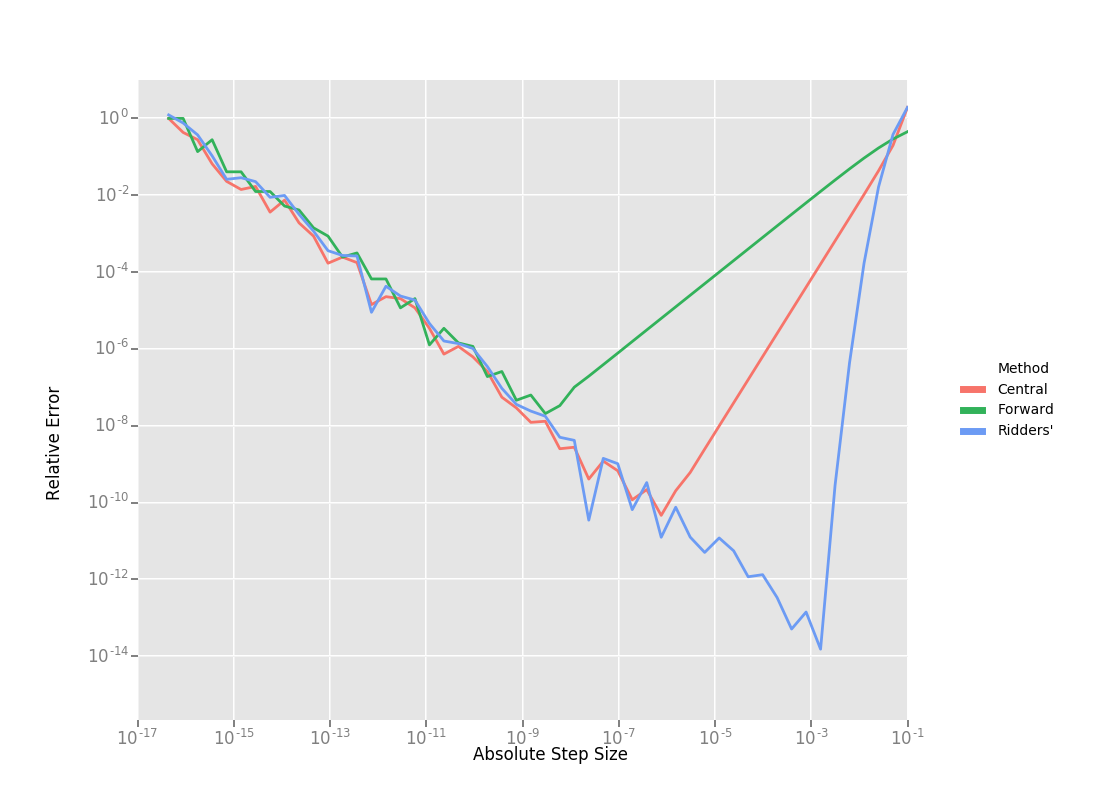
效果依次是 \(Ridders > Central > Forwad\) 。

• 第三种则是今天要介绍的主角，自动求导。

3.0 Ceres 自动求导原理

3.1 官方解释

其实官方对自动求导做出了解释，但是笔者觉得写的不够直观，比较抽象，不过既然是官方出品，还是非常有必要去看一看的。 http://ceres-solver.org/automatic_derivatives.html .

3.2 自我理解

\(\quad\) 这里笔者根据网上和官方的资料整理了一下自己的理解。Ceres 自动求导的核心是运算符的重载与Ceres自有的 Jet 变量.

举一个例子:

函数 \(\mathrm{f}(\mathrm{x})=\mathrm{h}(\mathrm{x}) * \mathrm{~g}(\mathrm{x})\) , 他的目标函数值为 \(\mathrm{h}(\mathrm{x}) * \mathrm{~g}(\mathrm{x})\) , 导数为 。

其中 \(h(x)\) , \(g(x)\) 都是标量函数. 如果我们定义一种数据类型.

并且对于数据类型 Data，重载乘法运算符 。

令 \(h(x) =[h(x),{h(x)}' ] , g(x)=[g(x),{g(x)' }]\) 。 \(f(x)=h(x) * g(x)\) , 那么 f_x.derived 就是 \(f(x)\) 的导数， f_x.value 即为 \(f(x)\) 的数值。value 储存变量的函数值, derived 储存变量对 \(\mathrm{x}\) 的导数。类似，如果我们对数据类型 Data 重载所有可能用到的运算符. “ \(+- * / \log , \exp , \cdots\) ” 。那么在变量 \(h(x),g(x)\) 经过任意次运算后， \(result=h(x)+g(x)*h(x)+exp(h(x))…\) , 任然能获得函数值 result.value 和他的导数值 result.derived ，这就是Ceres 自动求导的原理.

上面讲的都是单一自变量的自动求导，对于多元函数 \(f(x_i)\) 。对于n 元函数，Data 里面的 double derived 就替换为 double* derived，derived[i] 为对于第i个自变量的导数值.

并且对于数据类型 Data，乘法运算符重载为 。

其余的运算符重载方法也做相应改变。这样对多元函数的自动求导问题也就解决了。Ceres 里面的Jet 数据类型类似于 这里Data 类型，并且Ceres 对Jet 数据类型进行了几乎所有数学运算符的重载，以达到自动求导的目的.

4.0 实践

• 以下所有的代码实现都已经开源
  https://github.com/weihaoysgs/bal_solver_sim_ceres

4.1 Jet 的实现

这里我们模仿 Ceres 实现了 Jet ，并准备了两个具体的示例程序，Jet 具体代码在 ceres_jet.hpp 中，包装成了一个头文件，在使用的时候进行调用即可。这里也包含了一个 ceres_rotation.hpp 的头文件，是为了我们的第二个例子实现。具体代码如下:

• ceres_jet.hpp

                        
                          #ifndef _CERES_JET_HPP__
#define _CERES_JET_HPP__
#include <math.h>
#include <stdio.h>

#include <eigen3/Eigen/Core>
#include <eigen3/Eigen/Dense>
#include <eigen3/Eigen/Sparse>
#include "eigen3/Eigen/Eigen"
#include "eigen3/Eigen/SparseQR"
#include <fstream>
#include <iostream>
#include <map>
#include <queue>
#include <set>
#include <vector>
#include "ceres_rotation.hpp"

#include "algorithm"
#include "stdlib.h"

template <int N>
struct jet
{
  Eigen::Matrix<double, N, 1> v;
  double a;
  jet() : a(0.0) {}
  jet(const double& value) : a(value) { v.setZero(); }
  EIGEN_STRONG_INLINE jet(const double& value,
                          const Eigen::Matrix<double, N, 1>& v_)
      : a(value), v(v_)
  {
  }
  jet(const double value, const int index)
  {
    v.setZero();
    a = value;
    v(index, 0) = 1.0;
  }
  void init(const double value, const int index)
  {
    v.setZero();
    a = value;
    v(index, 0) = 1.0;
  }
};
/****************jet overload******************/
// for the camera BA,the autodiff only need overload the operator :jet+jet
// number+jet -jet jet-number jet*jet number/jet jet/jet sqrt(jet) cos(jet)
// sin(jet)  +=(jet) overload jet + jet
template <int N>
inline jet<N> operator+(const jet<N>& A, const jet<N>& B)
{
  return jet<N>(A.a + B.a, A.v + B.v);
}  // end jet+jet

// overload number + jet
template <int N>
inline jet<N> operator+(double A, const jet<N>& B)
{
  return jet<N>(A + B.a, B.v);
}  // end number+jet

template <int N>
inline jet<N> operator+(const jet<N>& B, double A)
{
  return jet<N>(A + B.a, B.v);
}  // end number+jet

// overload jet-number
template <int N>
inline jet<N> operator-(const jet<N>& A, double B)
{
  return jet<N>(A.a - B, A.v);
}
// overload number * jet because jet *jet need A.a *B.v+B.a*A.v.So the number
// *jet is required
template <int N>
inline jet<N> operator*(double A, const jet<N>& B)
{
  return jet<N>(A * B.a, A * B.v);
}
template <int N>
inline jet<N> operator*(const jet<N>& A, double B)
{
  return jet<N>(B * A.a, B * A.v);
}
// overload -jet
template <int N>
inline jet<N> operator-(const jet<N>& A)
{
  return jet<N>(-A.a, -A.v);
}
template <int N>
inline jet<N> operator-(double A, const jet<N>& B)
{
  return jet<N>(A - B.a, -B.v);
}
template <int N>
inline jet<N> operator-(const jet<N>& A, const jet<N>& B)
{
  return jet<N>(A.a - B.a, A.v - B.v);
}
// overload jet*jet
template <int N>
inline jet<N> operator*(const jet<N>& A, const jet<N>& B)
{
  return jet<N>(A.a * B.a, B.a * A.v + A.a * B.v);
}
// overload number/jet
template <int N>
inline jet<N> operator/(double A, const jet<N>& B)
{
  return jet<N>(A / B.a, -A * B.v / (B.a * B.a));
}
// overload jet/jet
template <int N>
inline jet<N> operator/(const jet<N>& A, const jet<N>& B)
{
  // This uses:
  //
  //   a + u   (a + u)(b - v)   (a + u)(b - v)
  //   ----- = -------------- = --------------
  //   b + v   (b + v)(b - v)        b^2
  //
  // which holds because v*v = 0.
  const double a_inverse = 1.0 / B.a;
  const double abyb = A.a * a_inverse;
  return jet<N>(abyb, (A.v - abyb * B.v) * a_inverse);
}
// sqrt(jet)
template <int N>
inline jet<N> sqrt(const jet<N>& A)
{
  double t = std::sqrt(A.a);

  return jet<N>(t, 1.0 / (2.0 * t) * A.v);
}
// cos(jet)
template <int N>
inline jet<N> cos(const jet<N>& A)
{
  return jet<N>(std::cos(A.a), -std::sin(A.a) * A.v);
}
template <int N>
inline jet<N> sin(const jet<N>& A)
{
  return jet<N>(std::sin(A.a), std::cos(A.a) * A.v);
}
template <int N>
inline bool operator>(const jet<N>& f, const jet<N>& g)
{
  return f.a > g.a;
}

#endif //_CERES_JET_HPP__

                        
                      

• ceres_rotation.hpp

                        
                          #ifndef CERES_ROTATION_HPP_
#define CERES_ROTATION_HPP_
#include <iostream>

template <typename T>
inline T DotProduct(const T x[3], const T y[3])
{
  return (x[0] * y[0] + x[1] * y[1] + x[2] * y[2]);
}

template <typename T>
inline void AngleAxisRotatePoint(const T angle_axis[3], const T pt[3],
                                 T result[3])
{
  const T theta2 = DotProduct(angle_axis, angle_axis);
  if (theta2 > T(std::numeric_limits<double>::epsilon()))
  {
    // Away from zero, use the rodriguez formula
    //
    //   result = pt costheta +
    //            (w x pt) * sintheta +
    //            w (w . pt) (1 - costheta)
    //
    // We want to be careful to only evaluate the square root if the
    // norm of the angle_axis vector is greater than zero. Otherwise
    // we get a division by zero.
    //
    const T theta = sqrt(theta2);
    const T costheta = cos(theta);
    const T sintheta = sin(theta);
    const T theta_inverse = T(1.0) / theta;

    const T w[3] = {angle_axis[0] * theta_inverse,
                    angle_axis[1] * theta_inverse,
                    angle_axis[2] * theta_inverse};

    // Explicitly inlined evaluation of the cross product for
    // performance reasons.
    const T w_cross_pt[3] = {w[1] * pt[2] - w[2] * pt[1],
                             w[2] * pt[0] - w[0] * pt[2],
                             w[0] * pt[1] - w[1] * pt[0]};
    const T tmp =
        (w[0] * pt[0] + w[1] * pt[1] + w[2] * pt[2]) * (T(1.0) - costheta);

    result[0] = pt[0] * costheta + w_cross_pt[0] * sintheta + w[0] * tmp;
    result[1] = pt[1] * costheta + w_cross_pt[1] * sintheta + w[1] * tmp;
    result[2] = pt[2] * costheta + w_cross_pt[2] * sintheta + w[2] * tmp;
  }
  else
  {
    // Near zero, the first order Taylor approximation of the rotation
    // matrix R corresponding to a vector w and angle w is
    //
    //   R = I + hat(w) * sin(theta)
    //
    // But sintheta ~ theta and theta * w = angle_axis, which gives us
    //
    //  R = I + hat(w)
    //
    // and actually performing multiplication with the point pt, gives us
    // R * pt = pt + w x pt.
    //
    // Switching to the Taylor expansion near zero provides meaningful
    // derivatives when evaluated using Jets.
    //
    // Explicitly inlined evaluation of the cross product for
    // performance reasons.
    const T w_cross_pt[3] = {angle_axis[1] * pt[2] - angle_axis[2] * pt[1],
                             angle_axis[2] * pt[0] - angle_axis[0] * pt[2],
                             angle_axis[0] * pt[1] - angle_axis[1] * pt[0]};

    result[0] = pt[0] + w_cross_pt[0];
    result[1] = pt[1] + w_cross_pt[1];
    result[2] = pt[2] + w_cross_pt[2];
  }
}

#endif  // CERES_ROTATION_HPP_

                        
                      

4.2 多项式函数自动求导

这里我们准备了两个实践案例，一个是对下面的函数进行自动求导，求在 \(f(1,2)\) 处的导数.

代码如下:

                        
                          #include <eigen3/Eigen/Core>
#include <eigen3/Eigen/Dense>

#include "ceres_jet.hpp"

int main(int argc, char const *argv[])
{
  /// f(x,y) = 2*x^2 + 3*y^3 + 3
  /// 残差的维度，变量1的维度，变量2的维度
  const int N = 1, N1 = 1, N2 = 1;
  Eigen::Matrix<double, N, N1> jacobian_parameter1;
  Eigen::Matrix<double, N, N2> jacobian_parameter2;
  Eigen::Matrix<double, N, 1> jacobi_residual;

  /// 模板参数为向量的维度，一定要是 N1+N2
  /// 也就是总的变量的维度，因为要存储结果（残差）
  /// 对于每个变量的导数值
  /// 至于为什么有 N1 个 jet 表示 var_x
  /// 假设变量 1 的维度为 N1,则残差对该变量的导数的维度是一个 N*N1 的矩阵
  /// 一个 jet<N1 + N2> 只能表示变量中的某一个在当前点的导数和值
  jet<N1 + N2> var_x[N1];
  jet<N1 + N2> var_y[N2];
	jet<N1 + N2> residual[N];
	/// 假设我们求上面的方程在 (x,y)->(1.0,2.0) 处的导数值
	double var_x_init_value[N1] = {1.0};
	double var_y_init_value[N1] = {2.0};

  for (int i = 0; i < N1; i++)
  {
    var_x[i].init(var_x_init_value[i], i);
  }
  for (int i = 0; i < N2; i++)
  {
    var_y[i].init(var_y_init_value[i], i + N1);
  }
	/// f(x,y) = 2*x^2 + 3*y^3 + 3
	/// f_x` = 4x
	/// f_y` = 9 * y^2
	residual[0] = 2.0 * var_x[0] * var_x[0]  + 3.0 * var_y[0] * var_y[0] * var_y[0] + 3.0;
	std::cout << "residual: " << residual[0].a << std::endl;
	std::cout << "jacobian: " << residual[0].v.transpose() << std::endl;
	/// residual: 29
	/// jacobian:  4 36
  return 0;
}

                        
                      

• 输出结果，读者可以自己求导算一下，是正确的.

                              
                                residual: 29
   jacobian:  4 36
  
                              
                            

4.3 BA 问题中的自动求导

这里是用的 Bal 数据集中的某个观测构建的误差项求导 。

                        
                          #include "ceres_jet.hpp"

class costfunction
{
 public:
  double x_;
  double y_;
  costfunction(double x, double y) : x_(x), y_(y) {}
  template <class T>
  void Evaluate(const T* camera, const T* point, T* residual)
  {
    T result[3];
    AngleAxisRotatePoint(camera, point, result);
    result[0] = result[0] + camera[3];
    result[1] = result[1] + camera[4];
    result[2] = result[2] + camera[5];
    T xp = -result[0] / result[2];
    T yp = -result[1] / result[2];
    T r2 = xp * xp + yp * yp;
    T distortion = 1.0 + r2 * (camera[7] + camera[8] * r2);
    T predicted_x = camera[6] * distortion * xp;
    T predicted_y = camera[6] * distortion * yp;
    residual[0] = predicted_x - x_;
    residual[1] = predicted_y - y_;
  }
};

int main(int argc, char const* argv[])
{
  const int N = 2, N1 = 9, N2 = 3;
  Eigen::Matrix<double, N, N1> jacobi_parameter_1;
  Eigen::Matrix<double, N, N2> jacobi_parameter_2;
  Eigen::Matrix<double, N, 1> jacobi_residual;
  costfunction* costfunction_ = new costfunction(-3.326500e+02, 2.620900e+02);
  jet<N1 + N2> cameraJet[N1];
  jet<N1 + N2> pointJet[N2];
  double params_1[N1] = {
      1.5741515942940262e-02,  -1.2790936163850642e-02, -4.4008498081980789e-03,
      -3.4093839577186584e-02, -1.0751387104921525e-01, 1.1202240291236032e+00,
      3.9975152639358436e+02,  -3.1770643852803579e-07, 5.8820490534594022e-13};
  double params_2[N2] = {-0.612000157172, 0.571759047760, -1.847081276455};
  for (int i = 0; i < N1; i++)
  {
    cameraJet[i].init(params_1[i], i);
  }
  for (int i = 0; i < N2; i++)
  {
    pointJet[i].init(params_2[i], i + N1);
  }
  jet<N1 + N2>* residual = new jet<N1 + N2>[N];
  costfunction_->Evaluate(cameraJet, pointJet, residual);
  for (int i = 0; i < N; i++)
  {
    jacobi_residual(i, 0) = residual[i].a;
  }
  for (int i = 0; i < N; i++)
  {
    jacobi_parameter_1.row(i) = residual[i].v.head(N1);
    jacobi_parameter_2.row(i) = residual[i].v.tail(N2);
  }
  /* 
  real result:
  jacobi_parameter_1: 
   -283.512    -1296.34    -320.603     551.177 0.000204691    -471.095   -0.854706    -409.362    -490.465
    1242.05      220.93    -332.566 0.000204691     551.177       376.9     0.68381     327.511     392.397
  jacobi_parameter_2: 
  545.118 -5.05828 -478.067
  2.32675  557.047  368.163
  jacobi_residual: 
  -9.02023
    11.264
   */
  std::cout << "jacobi_parameter_1: \n" << jacobi_parameter_1 << std::endl;
  std::cout << "jacobi_parameter_2: \n" << jacobi_parameter_2 << std::endl;
  std::cout << "jacobi_residual: \n" << jacobi_residual << std::endl;
  delete (residual);
  return 0;
}


                        
                      

• 输出结果 。

                              
                                jacobi_parameter_1: 
     -283.512    -1296.34    -320.603     551.177 0.000204691    -471.095   -0.854706    -409.362    -490.465
      1242.05      220.93    -332.566 0.000204691     551.177       376.9     0.68381     327.511     392.397
  jacobi_parameter_2: 
   545.118 -5.05828 -478.067
   2.32675  557.047  368.163
  jacobi_residual: 
  -9.02023
    11.264
  
                              
                            

Reference

• http://ceres-solver.org/
• https://blog.csdn.net/u012260559/article/details/105878468
• https://www.ngui.cc/article/show-902862.html?action=onClick

最后此篇关于Ceres自动求导解析-从原理到实践的文章就讲到这里了,如果你想了解更多关于Ceres自动求导解析-从原理到实践的内容请搜索CFSDN的文章或继续浏览相关文章，希望大家以后支持我的博客！ 。