前言

说到矩阵变换，我们第一时间想到的就是大学时代的线性代数这些复杂的东西，突然有了一种令人从入门到放弃的念头，不慌，作为了一个应用层的CV工程师， 在实际应用中线性代数哪些复杂的计算根本不用我们自己去算，绝大部分情境下直接使用 Matrix 这个类或者 glm 这个库即可.

关于矩阵与向量的相关知识，矩阵的加减乘除等规则，这里就不展开细说，感兴趣的同学自行查阅线性代数即可，不过这些规则忘记了也没关系，反正有API可用.

我们知道在Opengl中有很多中坐标系，在Opengl中矩阵的一大作用就是将坐标从一个坐标系转换到另一个坐标系下，同时还可以通过矩阵实现一些形变的效果， 今天我们就使用矩阵的方式搭配Opengl ES实现平移、缩放、旋转等一些形变变换的效果.

通常来说在Opengl ES中的矩阵都是一个4X4的矩阵，也就是一个包含16个元素的一维数组.

下面以 Matrix 这个类介绍一下矩阵变换的一些常用方法。下面介绍的矩阵变换所参考的坐标系统都是一样的，均是下图这个:

单位矩阵

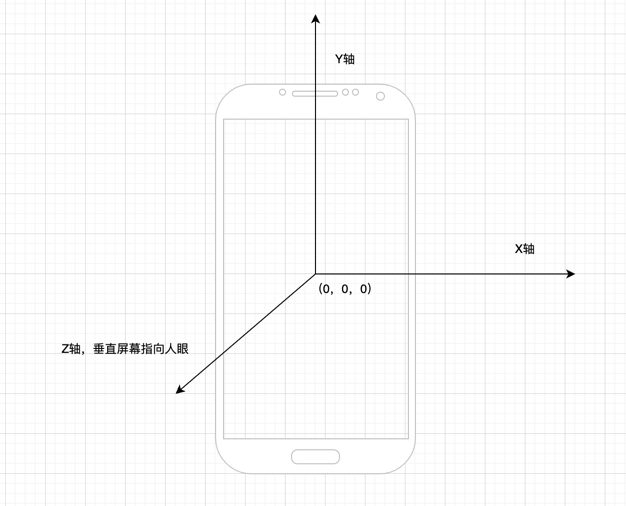
所谓的单位矩阵就是左上角到右下角对角线值均为1的矩阵，又成为单元矩阵。使用 Matrix.setIdentityM 方法可以将一个矩阵变为单位矩阵.

矩阵平移

矩阵平移所使用的方法是 Matrix.translateM .

需要注意的是在Opengl在顶点坐标的值是在-1到1之间，因此translateX的范围可以为-2到2。为什么呢？因为-1到1的距离是2，因此往最多可以往左移动2，同理，最多可以往右移动2.

矩阵旋转

矩阵旋转所使用的方法是 Matrix.rotateM ，其中第三个参数是表示选旋转的角度，后面的三个参数xyz代表的是绕那个轴旋转，绕那个轴旋转就把那个轴的参数设置成1，其他轴设置成0即可.

矩阵缩放

矩阵缩放所使用的方法是 Matrix.scaleM 。

组合矩阵的写法

假如有以下形变步骤，先绕Z轴旋转90度，再向X轴平移0.5，最后X轴缩放0.9倍，那么最终这个形变矩阵该如何计算呢？是以下这个写法吗?

                        
                          Matrix.rotateM(mvpMatrix, 0, 90, 0, 0, 1);
Matrix.translateM(mvpMatrix, 0, 0.5, 0, 0);
Matrix.scaleM(mvpMatrix, 0, 0.9, 1f, 0f);

                        
                      

不是的，组合矩阵的写法有一个规则，这个规则大家一定要记住:

在组合矩阵时，先进行缩放操作，然后是旋转，最后才是位移，但是写法需要反正写，也就是先写translateM，然后rotateM，最后scaleM 。

如果不这样写会发生什么呢？例如顺着写，先写scaleM，然后是rotateM，最后写translateM，测试时就会出现问题，旋转超过180度之后再移动，就会出现移动方向相反的情况.

因此以上例子正确的写法应该是这样子的:

                        
                          Matrix.translateM(mvpMatrix, 0, 0.5, 0, 0);
Matrix.rotateM(mvpMatrix, 0, 90, 0, 0, 1);
Matrix.scaleM(mvpMatrix, 0, 0.9, 1f, 0f);

                        
                      

show me code

在Opengl ES中可以使用 mat4 来表示一个4X4的矩阵，我们将总的变换矩阵在CPU中计算好之后以 uniform 的形式传递到着色器中去。 在顶点着色器中将矩阵与顶点坐标相乘的结果作为新的顶点输出坐标即可完成矩阵变换.

以下是MatrixTransformOpengl.cpp的详细代码:

                        
                          // 顶点着色器
static const char *ver = "#version 300 es\n"
                         "in vec4 aPosition;\n"
                         "in vec2 aTexCoord;\n"
                         "out vec2 TexCoord;\n"
                         "uniform mat4 mvpMatrix;\n"
                         "void main() {\n"
                         "  TexCoord = aTexCoord;\n"
                         "  gl_Position = mvpMatrix * aPosition;\n"
                         "}";

// 片元着色器
static const char *fragment = "#version 300 es\n"
                              "precision mediump float;\n"
                              "out vec4 FragColor;\n"
                              "in vec2 TexCoord;\n"
                              "uniform sampler2D ourTexture;\n"
                              "void main()\n"
                              "{\n"
                              "    FragColor = texture(ourTexture, TexCoord);\n"
                              "}";


// 使用绘制两个三角形组成一个矩形的形式(三角形带)
// 第一第二第三个点组成一个三角形，第二第三第四个点组成一个三角形
const static GLfloat VERTICES[] = {
        1.0f,-1.0f, // 右下
        1.0f,1.0f, // 右上
        -1.0f,-1.0f, // 左下
        -1.0f,1.0f // 左上
};

// 贴图纹理坐标（参考手机屏幕坐标系统，原点在左上角）
//由于对一个OpenGL纹理来说，它没有内在的方向性，因此我们可以使用不同的坐标把它定向到任何我们喜欢的方向上，然而大多数计算机图像都有一个默认的方向，它们通常被规定为y轴向下，X轴向右
const static GLfloat TEXTURE_COORD[] = {
        1.0f,1.0f, // 右下
        1.0f,0.0f, // 右上
        0.0f,1.0f, // 左下
        0.0f,0.0f // 左上
};

MatrixTransformOpengl::MatrixTransformOpengl():BaseOpengl() {
    initGlProgram(ver,fragment);
    positionHandle = glGetAttribLocation(program,"aPosition");
    textureHandle = glGetAttribLocation(program,"aTexCoord");
    textureSampler = glGetUniformLocation(program,"ourTexture");
    matrixHandle = glGetUniformLocation(program,"mvpMatrix");
}

MatrixTransformOpengl::~MatrixTransformOpengl() noexcept {
    LOGD("MatrixTransformOpengl析构函数");
}

void MatrixTransformOpengl::setMvpMatrix(float *mvp) {
    for (int i = 0; i < 16; ++i) {
        mvpMatrix[i] = mvp[i];
    }
}

void MatrixTransformOpengl::setPixel(void *data, int width, int height, int length) {
    LOGD("texture setPixel");
    imageWidth = width;
    imageHeight = height;
    glGenTextures(1, &textureId);

    // 激活纹理，注意以下这个两句是搭配的，glActiveTexture激活的是那个纹理，就设置的sampler2D是那个
    // 默认是0，如果不是0的话，需要在onDraw的时候重新激活一下？
//    glActiveTexture(GL_TEXTURE0);
//    glUniform1i(textureSampler, 0);

// 例如，一样的
    glActiveTexture(GL_TEXTURE2);
    glUniform1i(textureSampler, 2);
    // 绑定纹理
    glBindTexture(GL_TEXTURE_2D, textureId);
    // 为当前绑定的纹理对象设置环绕、过滤方式
    glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_S, GL_REPEAT);
    glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_WRAP_T, GL_REPEAT);
    glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MIN_FILTER, GL_LINEAR);
    glTexParameteri(GL_TEXTURE_2D, GL_TEXTURE_MAG_FILTER, GL_LINEAR);

    glTexImage2D(GL_TEXTURE_2D, 0, GL_RGBA, width, height, 0, GL_RGBA, GL_UNSIGNED_BYTE, data);
    // 生成mip贴图
    glGenerateMipmap(GL_TEXTURE_2D);

    glBindTexture(GL_TEXTURE_2D, textureId);

    // 解绑定
    glBindTexture(GL_TEXTURE_2D, 0);
}

void MatrixTransformOpengl::onDraw() {

//    glViewport(0,0,imageWidth,imageHeight);

    glClearColor(0.0f, 1.0f, 0.0f, 1.0f);
    glClear(GL_COLOR_BUFFER_BIT);
    glUseProgram(program);

    // 激活纹理
    glActiveTexture(GL_TEXTURE2);
    glUniform1i(textureSampler, 2);

    // 绑定纹理
    glBindTexture(GL_TEXTURE_2D, textureId);

    // 设置矩阵
    glUniformMatrix4fv(matrixHandle, 1, GL_FALSE,mvpMatrix);

    /**
     * size 几个数字表示一个点，显示是两个数字表示一个点
     * normalized 是否需要归一化，不用，这里已经归一化了
     * stride 步长，连续顶点之间的间隔，如果顶点直接是连续的，也可填0
     */
    // 启用顶点数据
    glEnableVertexAttribArray(positionHandle);
    glVertexAttribPointer(positionHandle,2,GL_FLOAT,GL_FALSE,0,VERTICES);

    // 纹理坐标
    glEnableVertexAttribArray(textureHandle);
    glVertexAttribPointer(textureHandle,2,GL_FLOAT,GL_FALSE,0,TEXTURE_COORD);

    // 4个顶点绘制两个三角形组成矩形
    glDrawArrays(GL_TRIANGLE_STRIP,0,4);

    glUseProgram(0);

    // 禁用顶点
    glDisableVertexAttribArray(positionHandle);
    if(nullptr != eglHelper){
        eglHelper->swapBuffers();
    }

    glBindTexture(GL_TEXTURE_2D, 0);
}

                        
                      

java层的MatrixActivity.java实例代码如下:

                        
                          public class MatrixActivity extends BaseGlActivity {

    private MatrixTransformOpengl matrixTransformOpengl;
    // 遵守先缩放再旋转最后平移的顺序
    // 首先执行缩放，接着旋转，最后才是平移。这就是矩阵乘法的工作方式。
    private final float[] mvpMatrix = new float[16];
    // 因为在Opengl在顶点坐标的值是在-1到1之间，因此translateX的范围可以为-2到2。
    private float translateX = 0;
    private float scaleX = 1;
    private float rotationZ = 0;

    @Override
    public int getLayoutId() {
        return R.layout.activity_gl_matrix;
    }

    @Override
    public BaseOpengl createOpengl() {
        matrixTransformOpengl = new MatrixTransformOpengl();
        return matrixTransformOpengl;
    }

    @Override
    public Bitmap requestBitmap() {
        BitmapFactory.Options options = new BitmapFactory.Options();
        // 不缩放
        options.inScaled = false;
        Bitmap bitmap = BitmapFactory.decodeResource(getResources(), R.mipmap.ic_boy, options);

        // 设置一下矩阵
        Matrix.setIdentityM(mvpMatrix, 0);
        matrixTransformOpengl.setMvpMatrix(mvpMatrix);

        return bitmap;
    }

    @Override
    protected void onCreate(@Nullable Bundle savedInstanceState) {
        super.onCreate(savedInstanceState);
        findViewById(R.id.bt_translate).setOnClickListener(new View.OnClickListener() {
            @Override
            public void onClick(View view) {
                if (null != matrixTransformOpengl) {
                    translateX += 0.1;
                    if(translateX >=2 ){
                        translateX = 0f;
                    }
                    updateMatrix();
                }
            }
        });

        findViewById(R.id.bt_scale).setOnClickListener(new View.OnClickListener() {
            @Override
            public void onClick(View view) {
                if (null != matrixTransformOpengl) {
                    scaleX += 0.1;
                    updateMatrix();
                }
            }
        });

        findViewById(R.id.bt_rotate).setOnClickListener(new View.OnClickListener() {
            @Override
            public void onClick(View view) {
                if (null != matrixTransformOpengl) {
                    rotationZ += 10;
                    updateMatrix();
                }
            }
        });

        findViewById(R.id.bt_reset).setOnClickListener(new View.OnClickListener() {
            @Override
            public void onClick(View view) {
                if (null != matrixTransformOpengl) {
                    translateX = 0;
                    scaleX = 1;
                    rotationZ = 0;
                    updateMatrix();
                }
            }
        });

    }

    private void updateMatrix() {
        Matrix.setIdentityM(mvpMatrix, 0);
        // 重点注释
        // 在组合矩阵时，先进行缩放操作，然后是旋转，最后才是位移，但是写法需要反正写，也就是先写translateM，然后rotateM，最后scaleM
        // 如果不这样写会发生什么呢？例如顺这写，先写scaleM，然后是rotateM，最后写translateM，测试时就会出现问题，旋转超过180度之后再移动，就会出现移动方向相反的情况
        Matrix.translateM(mvpMatrix, 0, translateX, 0, 0);
        Matrix.rotateM(mvpMatrix, 0, rotationZ, 0, 0, 1);
        Matrix.scaleM(mvpMatrix, 0, scaleX, 1f, 0f);
        matrixTransformOpengl.setMvpMatrix(mvpMatrix);
        myGLSurfaceView.requestRender();
    }
}

                        
                      

系列教程源码

https://github.com/feiflyer/NDK_OpenglES_Tutorial 。

后续demo如果有完善可能会更新.

Opengl ES系列入门介绍

Opengl ES之EGL环境搭建 Opengl ES之着色器 Opengl ES之三角形绘制 Opengl ES之四边形绘制 Opengl ES之纹理贴图 Opengl ES之VBO和VAO Opengl ES之EBO Opengl ES之FBO Opengl ES之PBO Opengl ES之YUV数据渲染 YUV转RGB的一些理论知识 Opengl ES之RGB转NV21 Opengl ES之踩坑记 Opengl ES之矩阵变换(上) Opengl ES之矩阵变换(下) Opengl ES之水印贴图 。

关注我，一起进步，人生不止coding！！！ 。

最后此篇关于OpenglES之矩阵变换(上)的文章就讲到这里了,如果你想了解更多关于OpenglES之矩阵变换(上)的内容请搜索CFSDN的文章或继续浏览相关文章，希望大家以后支持我的博客！ 。