对极几何、基本矩阵、本质矩阵

对极约束相关介绍可以在《计算机视觉中的多视图几何》一书的185页找到； 。

1 对极约束

1.2 对极约束的理解

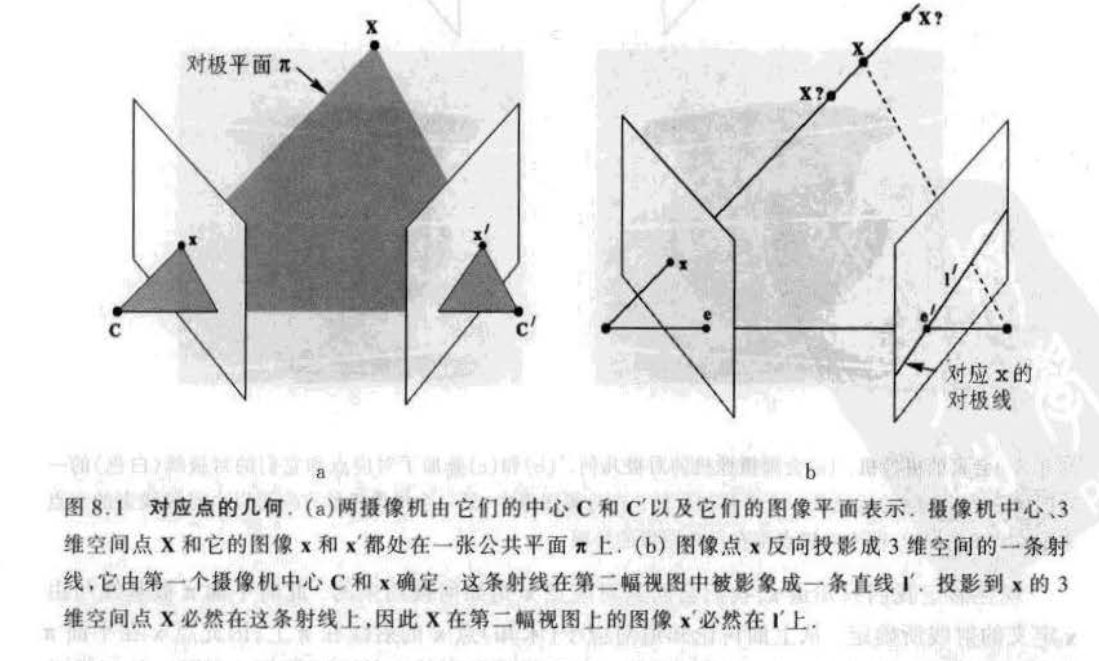
对极几何是两幅视图之间内在的射影几何； 。

对极约束：已知某一3D点 \(X\) 在第一张图像上的投影是 \(x\) ,那么在同样观测到点 \(X\) 的第二幅图像上的投影 \(x'\) 是如何被约束的?

首先，有相机投影模型 \(Zx = PX\) ，可以推断点 \(X\) 在射线 \(Cx\) 上，（C是第一个相机的光心） 。

由于无法确定点 \(X\) 的深度，因此，第二幅图像上成像点的在面 \(CC'X\) 与成像平面的交线 \(l'\) 上,在对极几何中称为极线 。

则有第一个摄像机光心在第二幅图像上的投影 \(e'\) 称为极点 。

因此：对极约束实际上是将 \(x'\) 约束在直线 \(l'\) 上，表示是由点 \(x\) 到直线 \(l'\) 的映射 。

假设 该映射为 \(F\) , 则有 \(l' = Fx\) ,由于点 \(x'\) 在直线 \(l'\) 上，可得 。

其中，映射 \(F\) 就是基本矩阵， 表示的是点到线的映射； 。

对极几何的前提：基线长度不能为0；初始化，纯旋转退化，对极约束就不存在了.

2 基本矩阵-Fundamental(对极约束的代数表示)

2.1 基本矩阵的几何推导

基本矩阵的几何推导的详细内容可以参考《计算机视觉中的多视图几何》 。

将对极约束的过程分成两步来分析:

1. 假设有虚拟平面 \(\pi\) ，将图像平面1上的点 \(x\) ，投影到平面 \(\pi\) 上，在转移到图像平面2上的点 \(x^{'}\)

1. 第二步是构造对极线，即摄影机 \(P_1\) 的光心在图像平面2上的投影-极点 \(e^{'}\) 和投影点 \(x^{'}\) 构成的直线 \(l^{'}\) ,两个点的叉乘得到直线方程；

那么可以定义点到极线的映射 \(F\) 满足： \(I^{'} = Fx\) ，因此， \(F = [e^{'}]_{\times}H_{\pi}\) ，由于 \([e^{'}]_{\times}\) 的秩为2，基本矩阵 \(F\) 的秩为2.

另外，由于点 \(x\) 的投影点 \(x^{'}\) 一定在直线 \(I^{'}\) 上，通过内积为0可以得到一个约束，也就是对极约束.

2.2 基本矩阵的代数推导

2.3 基本矩阵的重要性质

3 基本矩阵的计算方法

3.1 最小化代数距离方法（DLT）

3.2 退化情形

无平移，两个视图，摄影机中心重合。对极几何的定义不存在了 。

4 本质矩阵

4.1 对本质矩阵的理解

首先本质矩阵是基本矩阵在归一化平面上的特殊表示；具有形式: \(E = [t]_{*}R = R[R^{T}t]_{*}\) 。

4.2 本质矩阵的性质

(1) 本质矩阵的自由度

本质矩阵的自由度是 5 ，旋转矩阵和平移向量分别有三个自由度，但是本质矩阵有一个全局尺度因子的多义性； 。

(其实对自由度的理解还不是很透彻) 。

(2) 本质矩阵的内在性质

一个矩阵是本质矩阵的 充要条件 是它的奇异值中有两个相等而第三个是0.其奇异值一定是 \([\sigma,\sigma,0]^{T}\) 的形式 。

该结论的证明在《计算机视觉中的多视图几何》的9.6.1小节有介绍； 。

4.3 本质矩阵的求解

本质矩阵的求解也可以使用八点法，构建线性方程组来求解。具体的形式不再推导。可以参考《视觉SLAM十四讲》 。

值得提一下的是，八点法构建的线性方程组，最后求解完，可能没办法满足本质矩阵的内在性质 。

那有没有解决办法呢?

可以进行如下操作:

1. 首先对E做奇异值分解：假设得到E的奇异值矩阵 \(\Sigma = diag(\sigma_1,\sigma_2,\sigma_3)\) ,且有 \(\sigma_1 > \sigma_2 > \sigma_3\)
2. 那么可以取新的E为

4.4 本质矩阵的分解（由本质矩阵恢复摄像机矩阵）

对本质矩阵的分解，还不太理解； 。

可以参考《计算机视觉中的多视图几何》和《视觉SLAM十四讲》一起看； 。

在ORB-SLAM2的地图初始化时，会分别计算H和F，统计特征点重投影误差及点到极线的距离计算得分，选择得分高的映射.

当选择F矩阵时，需要从F矩阵中恢复位姿，ORB-SLAM2中会通过F计算E，再从E中恢复pose.

总结一下流程:

1. 对本质矩阵进行奇异值分解
2. 左奇异值矩阵U的最后一列就是t，对其进行归一化
3. 构造一个绕Z轴旋转pi/2的旋转矩阵W，按照下式组合得到旋转矩阵 R1 = u W vt，旋转矩阵有行列式为+1的约束，所以如果算出来为负值，需要取反
4. 矩阵W取转置来按照相同的公式计算旋转矩阵 R2 = u W.t() vt，同理，旋转矩阵有行列式为+1的约束，所以如果算出来为负值，需要取反
5. 获得本质矩阵分解结果，形成四组解,分别是： (R1, t) (R1, -t) (R2, t) (R2, -t)
6. 四组接分别进行三角化，取有效3D点最多的一组解。

                        
                          // step 2 : 根据基础矩阵和相机的内参数矩阵计算本质矩阵
  cv::Mat E21 = K.t()*F21*K;

  // 定义本质矩阵分解结果，形成四组解,分别是： (R1, t) (R1, -t) (R2, t) (R2, -t)
  cv::Mat R1, R2, t;

  // step 3 : 从本质矩阵求解两个R解和两个t解，共四组解
  // Note : 参考：Multiple View Geometry in Computer Vision - Result 9.19 p259
  // 不过由于两个t解互为相反数，因此这里先只获取一个
  // 虽然这个函数对t有归一化，但并没有决定单目整个SLAM过程的尺度.
  // 因为 CreateInitialMapMonocular 函数对3D点深度会缩放，然后反过来对 t 有改变.
  //注意下文中的符号“'”表示矩阵的转置
  //                          |0 -1  0|
  // E = U Sigma V'   let W = |1  0  0|
  //                          |0  0  1|
  // 得到4个解 E = [R|t]
  // R1 = UWV' R2 = UW'V' t1 = U3 t2 = -U3
  DecomposeE(E21,R1,R2,t);
  cv::Mat t1 = t;
  cv::Mat t2 = -t;

                        
                      

                        
                          /**
 * @brief 分解Essential矩阵得到R,t
 * 分解E矩阵将得到4组解，这4组解分别为[R1,t],[R1,-t],[R2,t],[R2,-t]
 * 参考：Multiple View Geometry in Computer Vision - Result 9.19 p259
 * @param[in] E                 本质矩阵
 * @param[in & out] R1          旋转矩阵1
 * @param[in & out] R2          旋转矩阵2
 * @param[in & out] t           平移向量，另外一个取相反数
 */
void Initializer::DecomposeE(const cv::Mat &E, cv::Mat &R1, cv::Mat &R2, cv::Mat &t)
{
  // 准备存储对本质矩阵进行奇异值分解的结果
  cv::Mat u,w,vt;
  // 对本质矩阵进行奇异值分解
  cv::SVD::compute(E,w,u,vt);

  // 左奇异值矩阵U的最后一列就是t，对其进行归一化
  u.col(2).copyTo(t);
  t=t/cv::norm(t);

  // 构造一个绕Z轴旋转pi/2的旋转矩阵W，按照下式组合得到旋转矩阵 R1 = u*W*vt
  // 计算完成后要检查一下旋转矩阵行列式的数值，使其满足行列式为1的约束
  cv::Mat W(3,3,CV_32F,cv::Scalar(0));
  W.at<float>(0,1)=-1;
  W.at<float>(1,0)=1;
  W.at<float>(2,2)=1;

  // 计算
  R1 = u*W*vt;
  // 旋转矩阵有行列式为+1的约束，所以如果算出来为负值，需要取反
  if(cv::determinant(R1)<0)
    R1=-R1;

  // 同理将矩阵W取转置来按照相同的公式计算旋转矩阵R2 = u*W.t()*vt
  R2 = u*W.t()*vt;
  //旋转矩阵有行列式为1的约束
  if(cv::determinant(R2)<0)
    R2=-R2;
}

                        
                      

最后此篇关于学习分享：对极几何、基本矩阵、本质矩阵（持续更新）的文章就讲到这里了,如果你想了解更多关于学习分享：对极几何、基本矩阵、本质矩阵（持续更新）的内容请搜索CFSDN的文章或继续浏览相关文章，希望大家以后支持我的博客！ 。