- Java锁的逻辑(结合对象头和ObjectMonitor)
- 还在用饼状图?来瞧瞧这些炫酷的百分比可视化新图形(附代码实现)⛵
- 自动注册实体类到EntityFrameworkCore上下文,并适配ABP及ABPVNext
- 基于Sklearn机器学习代码实战
。
实现语言:C++ 。
线性表(Linear List) 。
是由n(n≥0)个具有 相同特性(数据类型) 的 数据元素(结点) a 1 ,a 2 ,...,a i-1, a i ,a i+1, ...,a n 组成的 有限序列 .
其中,a 1 为线性起点(起始结点),a n 为线性终点(终端结点)。对于每一个数据元素a i ,我们称a i-1 为它的直接前驱,a i+1 为它的直接后继。i(1≤i≤n)为下标,是元素的序号,表示元素在表中的位置;n为数据元素总个数,即表长。当n=0时,称线性表为空表.
线性表的存储结构 。
在计算机中,线性表有两种基本的存储结构: 顺序存储结构 和 链式存储结构 .
线性表的顺序表示又称为 顺序存储结构或顺序映像 。顺序存储,即把逻辑上相邻的数据元素存储在物理上相邻的存储单元中。其特点是 依次存储 , 地址连续 —— 中间没有空出存储单元,且任一元素可 随机存取 .
线性表的第一个数据元素a 1 的存储位置,称为线性表的起始位置或 基地址 .
顺序表中元素存储位置的计算 。
LOC(a i ) = LOC(a 1 ) + (i-1) x m (m为每个元素占用的存储单元) 。
每个元素的存取时间复杂度为O(1),我们称之为随机存取.
顺序表的表示 。
#define LIST_INIT_SIZE 100 // 线性表存储空间的初始分配量
typedef struct{
ElemType elem[LIST_INIT_SIZE];
int length; // 当前长度
}SqList;
例如:多项式 P n (x) = p 1 x e 1 + p 2 x e 2 + ... + p m x e m 的顺序存储结构类型定义如下:
#include <stdlib.h>
#define MAXSIZE 1000 // 多项式可能达到的最大长度
typedef struct { // 多项式非零项的定义
float p; // 系数
int e; // 指数
}Polynomial;
typedef struct {
Polynomial* data; // 存储空间的基地址
int length; // 多项式中当前项的个数
}SqList; // 多项式的顺序存储结构类型定义为SqList
int main(int argc, char** argv) {
SqList L;
// 开辟指定长度的地址空间,并返回这段空间的首地址
L.data = (Polynomial*)malloc(sizeof(Polynomial) * MAXSIZE);
// 释放申请的内存空间
free(L.data);
SqList L2;
// 动态申请存放Polynomial类型对象的内存空间,成功则返回Polynomial类型的指针,指向新分配的内存
L2.data = new Polynomial();
// 释放指针L2.data所指向的内存
delete L2.data;
return 0;
}
// 初始化顺序表(构造一个空的顺序表)
Status InitList_Sq(SqList& L) {
L.elem = new ElemType[MAXSIZE]; // 为顺序表分配存储空间
if (!L.elem) exit(OVERFLOW); // 存储分配失败
L.length = 0; // 空表长度为0
return OK;
}
// 销毁顺序表
void DestroyList(SqList& L) {
if(L.elem) delete L.elem; // 释放存储空间
}
// 清空线性表
void ClearList(SqList& L) {
L.length = 0; // 将顺序表的长度置0
}
// 求线性表的长度
int GetLength(SqList L) {
return (L.length);
}
// 判断顺序表L是否为空
int IsEmpty(SqList L) {
if (L.length == 0) return 1;
else return 0;
}
// 顺序表的取值(根据位置i获取相应位置数据元素的内容)
int GetElem(SqList L, int i, ElemType& e) {
if (i<1 || i>L.length) return 0;
e = L.elem[i - 1]; // 第i-1个单元存储着第i个数据
return 1;
}
顺序表初始化、销毁顺序表、清空顺序表、求顺序表长度、判断顺序表是否为空及顺序表的取值等操作,它们的 时间复杂度都为O(1) 。
// 顺序表的查找
int LocateElem(SqList L, ElemType e) {
for (int i = 0; i < L.length; i++) {
if (L.elem[i] == e)
return i + 1;
}
return 0;
}
平均查找长度ASL(Average Search Length): 为确定记录在表中的位置,需要与给定值进行比较的关键字的个数的期望值叫做查找算法的平均查找长度.
含有n个记录的表,查找成功时:
ASL = 1/n * (1+2+...+n) = (n+1)/2 。
所以,顺序表查找算法的 平均时间复杂度为:O(n) 。
【算法思路】 。
【代码】 。
// 顺序表的插入(在顺序表L的第i个位置插入元素e)
int ListInsert(SqList& L, int i, ElemType e) {
L.length += 1;
if (i <= 0 || i > L.length + 1) return 0; // 判断i值是否合法
if (L.length == MAXSIZE) return 0; // 判断当前存储空间是否已满
for (int k = L.length - 1; k >= i - 1; k--)
L.elem[k + 1] = L.elem[k]; // 插入位置及之后的元素后移
L.elem[i-1] = e;
L.length ++;
return 1;
}
【算法分析】 。
算法时间主要耗费在移动元素的操作上.
若插入在尾结点之后,则需要移动0次;若插入在首结点之前,则需要移动n次;在各个位置插入(共n+1种可能)的平均移动次数为:E = 1/(n+1) * (0+1+...+n) = n/2 。
所以,顺序表插入算法的 平均时间复杂度为: O(n) 。
【算法思路】 。
【代码】 。
// 顺序表的删除(删除顺序表L第i个位置的元素e)
int ListDelete(SqList& L, int i, ElemType& e) {
if (i < 1 || i > L.length) return 0; // 判断i值是否合法(1<=i<=L.length)
for (int k = i; k < L.length - 1; k++)
L.elem[k - 1] = L.elem[k]; // 被删除之后的元素前移
L.length--;
return 1;
}
【算法分析】 。
算法时间主要耗费在移动元素的操作上.
若删除尾结点,则需要移动0次;若删除首结点,则需要移动n-1次;在各个位置删除(共n种可能)的平均移动次数为:E = 1/n * (0+1+...+n-1) = (n-1)/2 。
所以,顺序表删除算法的 平均 时间复杂度 为:O(n) 。
由于没有占用辅助空间,顺序表所有操作的 空间复杂度都为:O(1) 。
优点:
缺点:
链式存储结构又称为非顺序映像或链式映像。其特点是:
链式存储相关术语:
Q1:如何表示空表?
Q2:在链表中附设头结点有什么好处?
Q3:头结点的数据域内装的是什么?
头结点的数据域可以为空,也可以存放线性表长度等附加信息,但此结点不能计入链表长度值.
单链表是由表头唯一确定,因此单链表可以用头指针的名字来命名。若头指针名为L,则把链表称为表L.
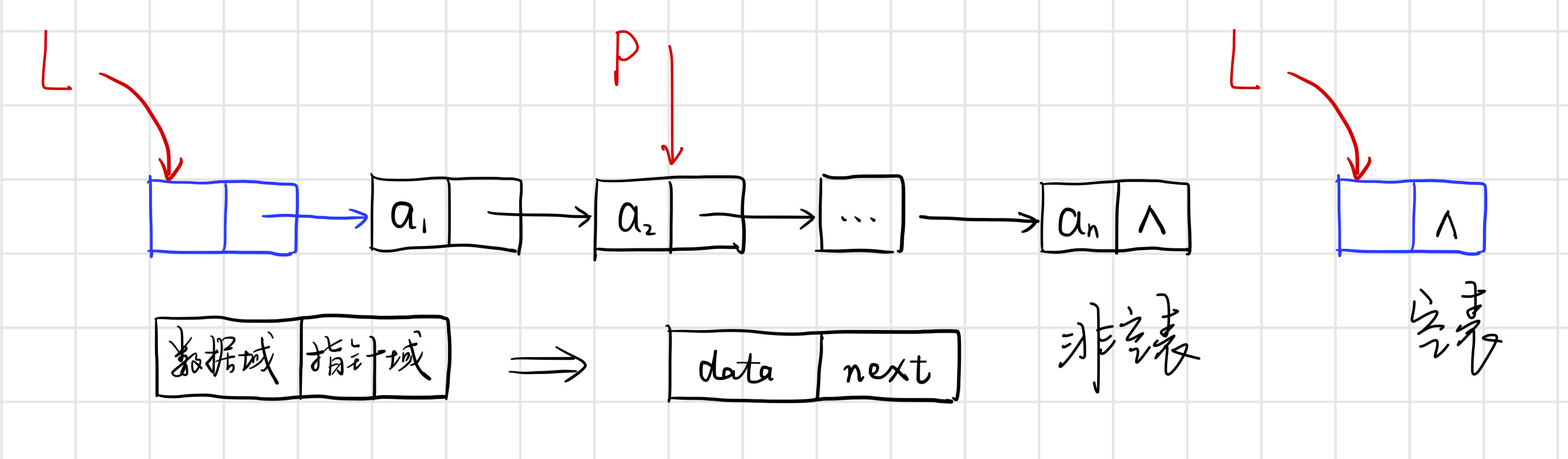
单链表的存储结构 。
typedef char ElemType;
typedef struct Lnode { // 声明结点的数据类型和指向结点的指针类型
ElemType data; // 结点的数据域
struct Lnode* next; // 结点的指针域
}Lnode, *LinkList; // LinkList为指向结构体Lnode的指针类型
定义链表和节点指针可以用 LinkList L; 或LNode* L,
这两种方式等价,但为了表述清晰,一般建议使用LinkList定义链表,Lnode定义结点指针。即:
定义链表:LinkList L,
定义节点指针:Lnode* p,
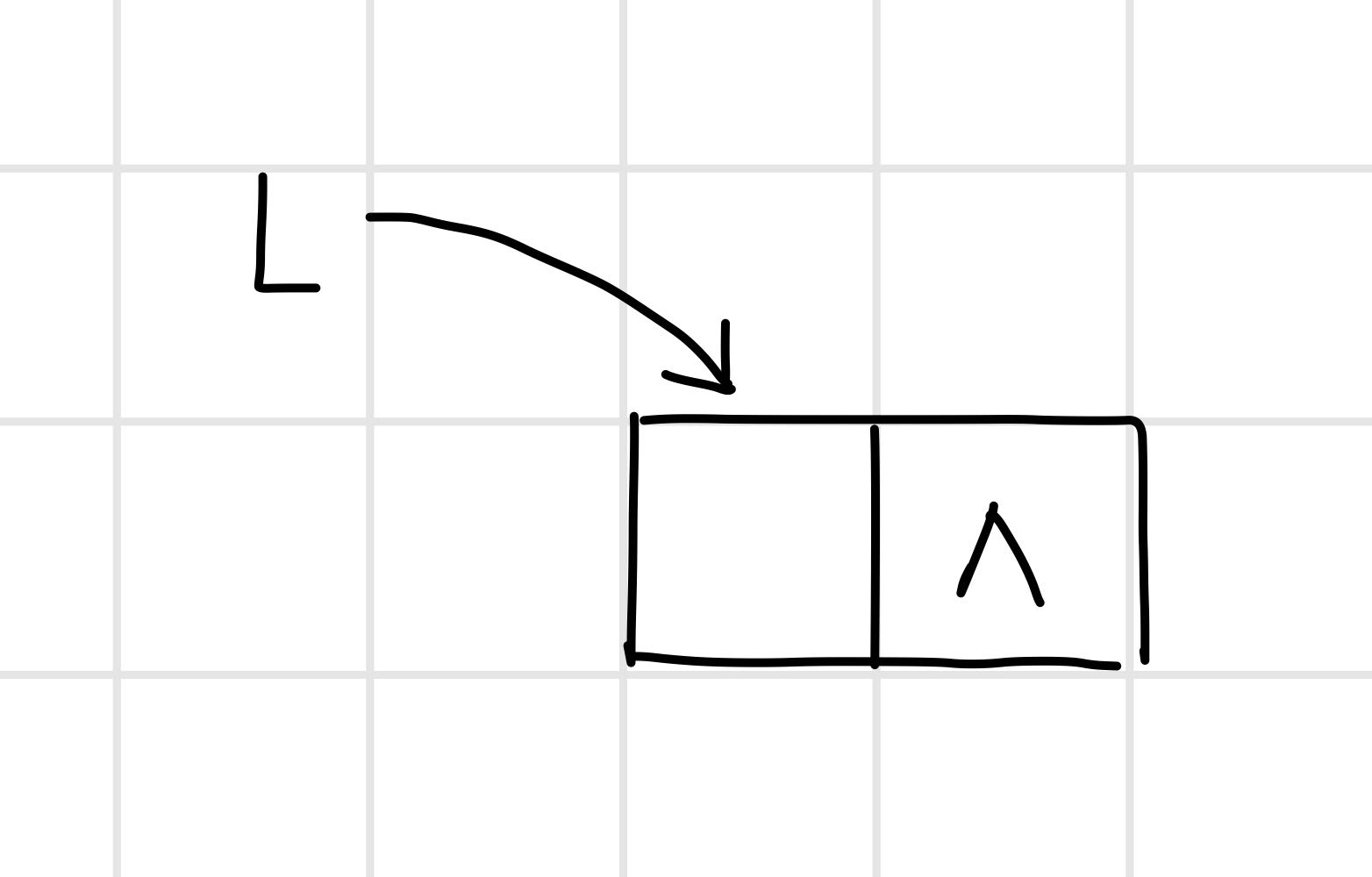
即构造一个如图的空表:
【算法思路】 。
【代码】 。
// 单链表的初始化(带头结点)
int InitList(LinkList& L) {
L = new LNode; // 或L = (LinkList)malloc(sizeof(LNode));
L->next= NULL;
return 1;
}
【算法思路】 。
判断头结点指针域是否为空.
【代码】 。
int ListEmpty(LinkList L) {
if (L->next)
return 0;
else
return 1;
}
【算法思路】 。
从头指针开始,依次释放所有节点.
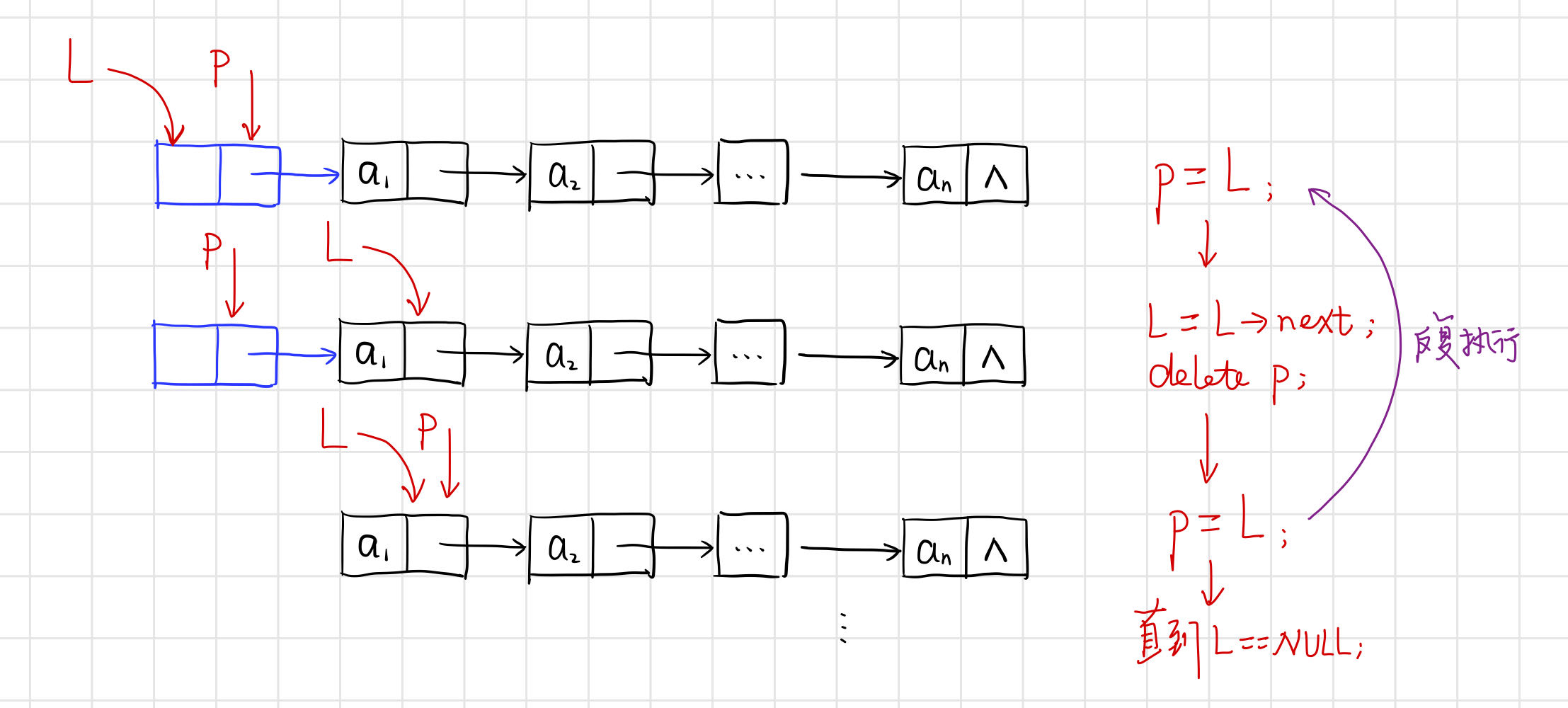
【代码】 。
// 单链表的销毁
int DestroyList_L(LinkList& L) {
Lnode* p;
while (L) {
p = L;
L = (LinkList)L->next;
delete p;
}
return 1;
}
【算法思路】 。
从首元结点开始,依次释放所有结点,并将头结点指针域设置为空.

【代码】 。
// 清空单链表
int ClearList(LinkList& L) {
Lnode *p, *q;
p = (Lnode*)L->next;
while (L) {
q = (Lnode*)p->next;
delete p;
p = q;
}
L->next = nullptr;
}
【算法思路】 。
从首元结点开始,依次计数所有结点.
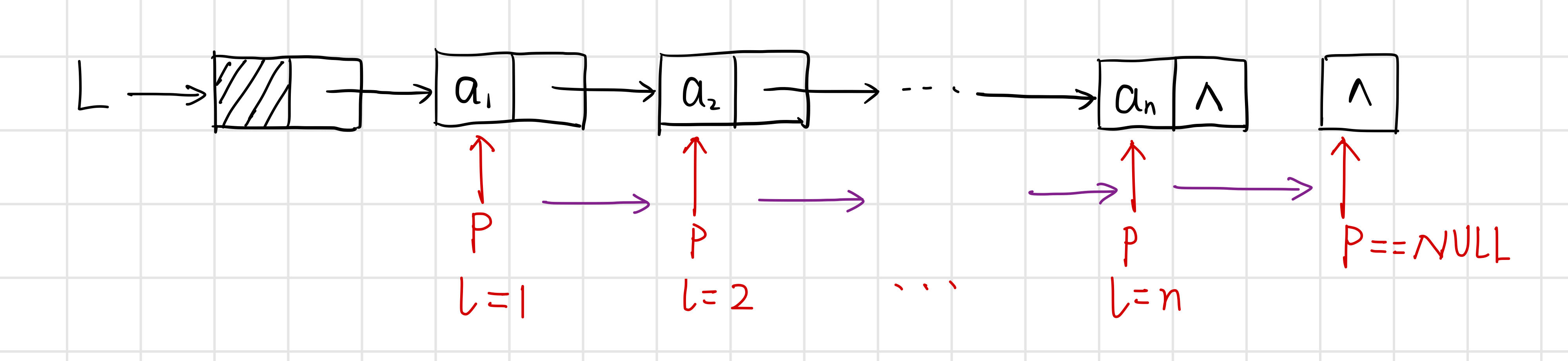
【代码】 。
// 求单链表的表长
int ListLength(LinkList L) {
Lnode* p;
int len;
p = (Lnode*)L->next; // p指向第一个结点(首元结点)
while (p) {
len++;
p = (Lnode*)p->next;
}
return len;
}
【算法思路】 。
从链表的头指针出发,顺着链域next逐个结点往下搜索,直至搜索到第i个结点位置。我们称之为 顺序存取 .
【代码】 。
// 取值:取单链表中第i个元素的内容,通过变量e返回
int GetElem(LinkList L, int i, ElemType& e)
{
Lnode* p;
p = (Lnode*)L->next;
int j = 1;
while (p && j < i) { // 向后扫描,直到p指向第i个元素或p为空
p = (Lnode*)p->next;
j++;
}
// 第i个元素不存在,分三种情况:i<1,i超过表长,L为空表)
if (!p || i < 1) return 0;
e = p->data;
return 1;
}
【算法思路】 。
【代码】 。
// 按值查找—根据指定数据获取该数据所在的位置(地址)
Lnode* LocateElemAddress(LinkList L, ElemType e) {
Lnode* p = (Lnode*)L->next;
while (p && p->data != e)
p = (Lnode*)p->next;
// if (!p) return nullptr; // 空表或未查找到返回NULL
return p;
}
// 按值查找—根据指定数据获取该数据的位置序号
int LocateElemIndex(LinkList L, ElemType e) {
Lnode* p = (Lnode*)L->next;
int j = 1;
while (p && p->data != e) {
p = (Lnode*)p->next;
j++;
}
if (!p) return 0; // 空表或未查找到返回0
return j;
}
【算法分析】 。
因线性链表只能顺序存取,即在查找时要从头指针找起,因此查找的 时间复杂度为:O(n) 。
【算法思路】 。
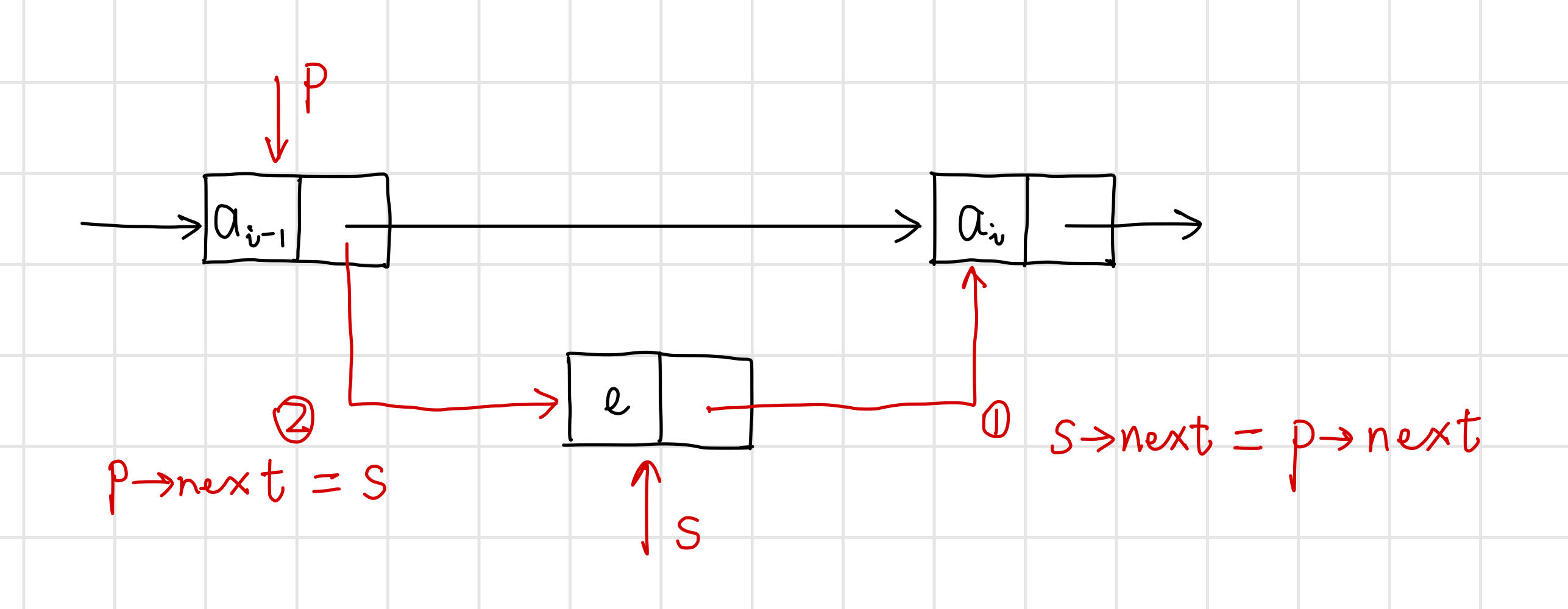
【代码】 。
// 在单链表L中第i个元素之前插入数据元素e
int ListInsert(LinkList& L, int i, ElemType e) {
// 先找到第i-1个元素的位置
Lnode* p = L;
int j = 0;
while (p && j < i - 1) {
p = (Lnode*)p->next;
j++;
}
if (!p || i < 1) return 0; // i<1或i超过表长+1,插入位置非法
// 将结点s插入L中
LinkList s = new Lnode; // 生成新结点s
s->data = e; // 结点s的数据域置为e
s->next = p->next; // 新结点s指针域指向第i个结点
p->next = s; // 第i-1个结点的指针域指向新结点s
return 1;
}
【算法分析】 。
在编译 p->next = s 这句代码是会报异常: “不能将Lnode*类型的值分配到Lnode类型的实体” .
因线性链表不需要移动元素,只要修改指针,一般情况下插入操作的时间复杂度为: O(1) 。但是,如果要在单链表中进行前插操作,由于要从头查找前驱结点,其时间复杂度为: O(n) .
【算法思路】 。
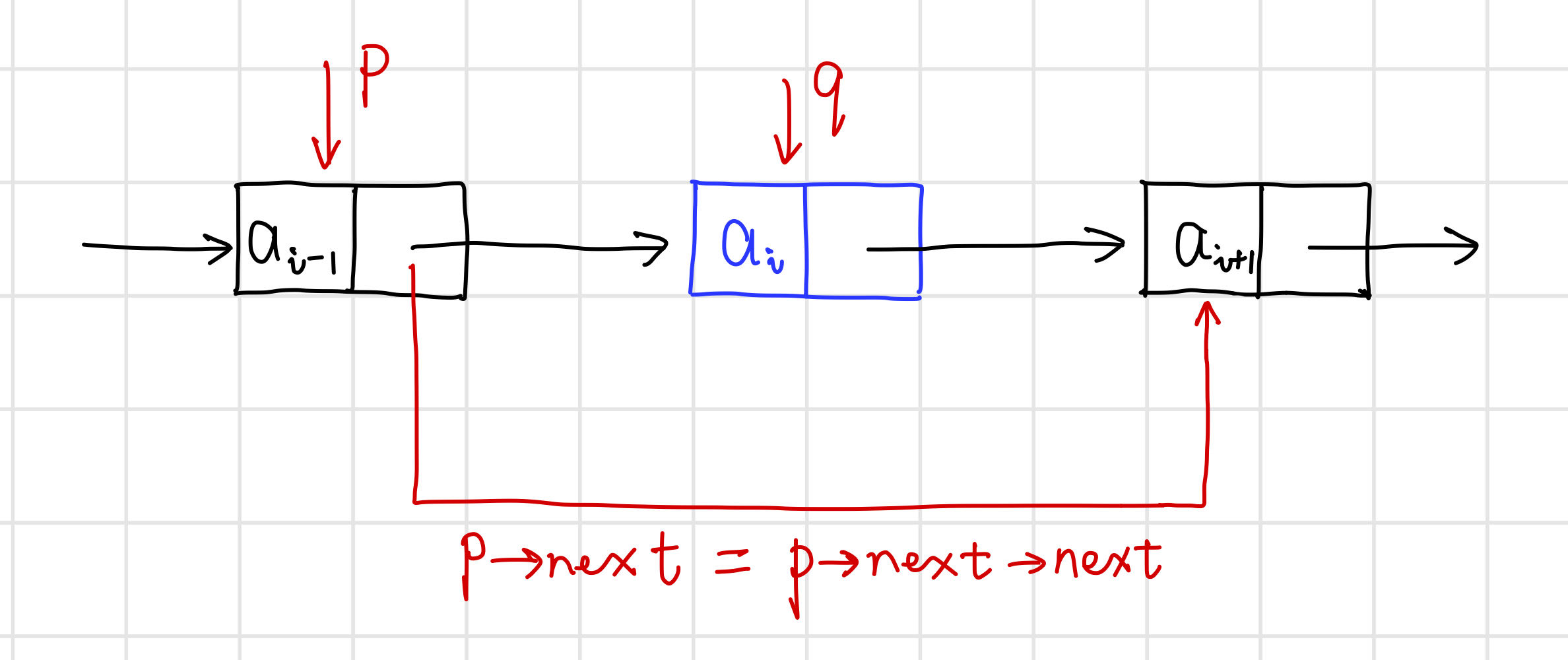
【代码】 。
// 删除单链表L中第i个数据元素(结点)
int ListDelete(LinkList& L, int i, ElemType& e) {
// 先找到第i-1个元素的位置
Lnode* p = L;
int j = 0;
while (p && j < i - 1) {
p = (Lnode*)p->next;
j++;
}
if (!p || i < 1) return 0; // i<1或i超过表长,删除位置非法
// 删除第i个结点
Lnode* q = (Lnode*)p->next; // 临时保存被删结点的地址以备释放
p->next = q->next; // 改变删除结点前驱结点的指针域
e = q->data; // 保存删除结点的数据域
delete q; // 释放删除结点的空间
return 1;
}
【算法分析】 。
其时间复杂度和插入操作一致.
(1)头插法——元素插入在链表头部,也叫前插法.
【算法思路】 。
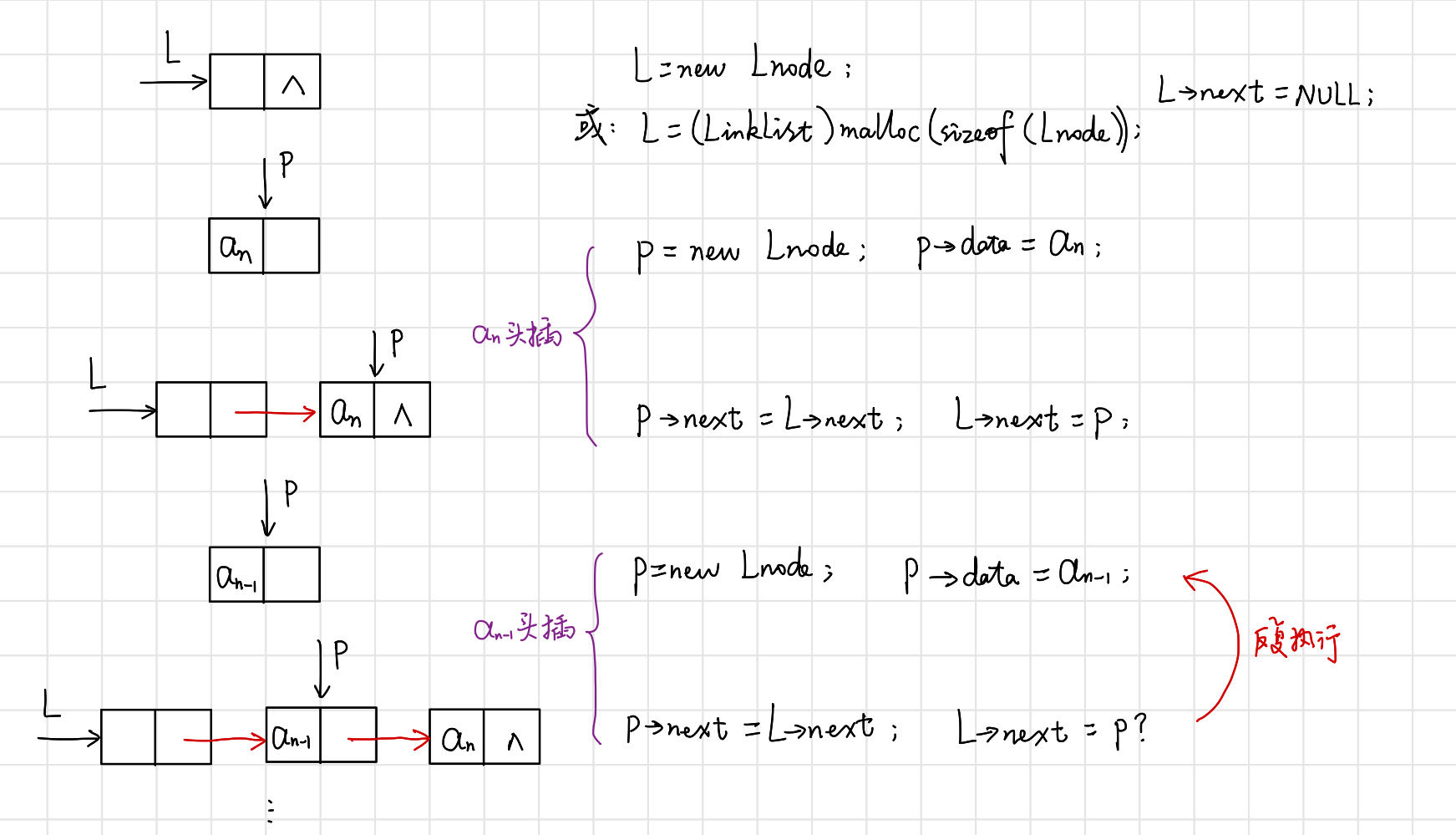
【代码】 。
// 建立单链表:头插法
void CreateList(LinkList& L, int n) {
L = new Lnode;
L->next = nullptr;
for (int i = n; i > 0; i--) {
Lnode* p = new Lnode; // 输入新结点 p = (Lnode*)malloc(sizeof(Lnode));
std::cin >> p->data; // 输入元素值 scanf(&p->data);
p ->next = L->next; // 插入到表头
L->next = p; // 不能将Lnode*类型的值分配到Lnode类型的实体
}
}
(2)尾插法——元素插入在链表尾部,也叫后插法.
【算法思路】 。
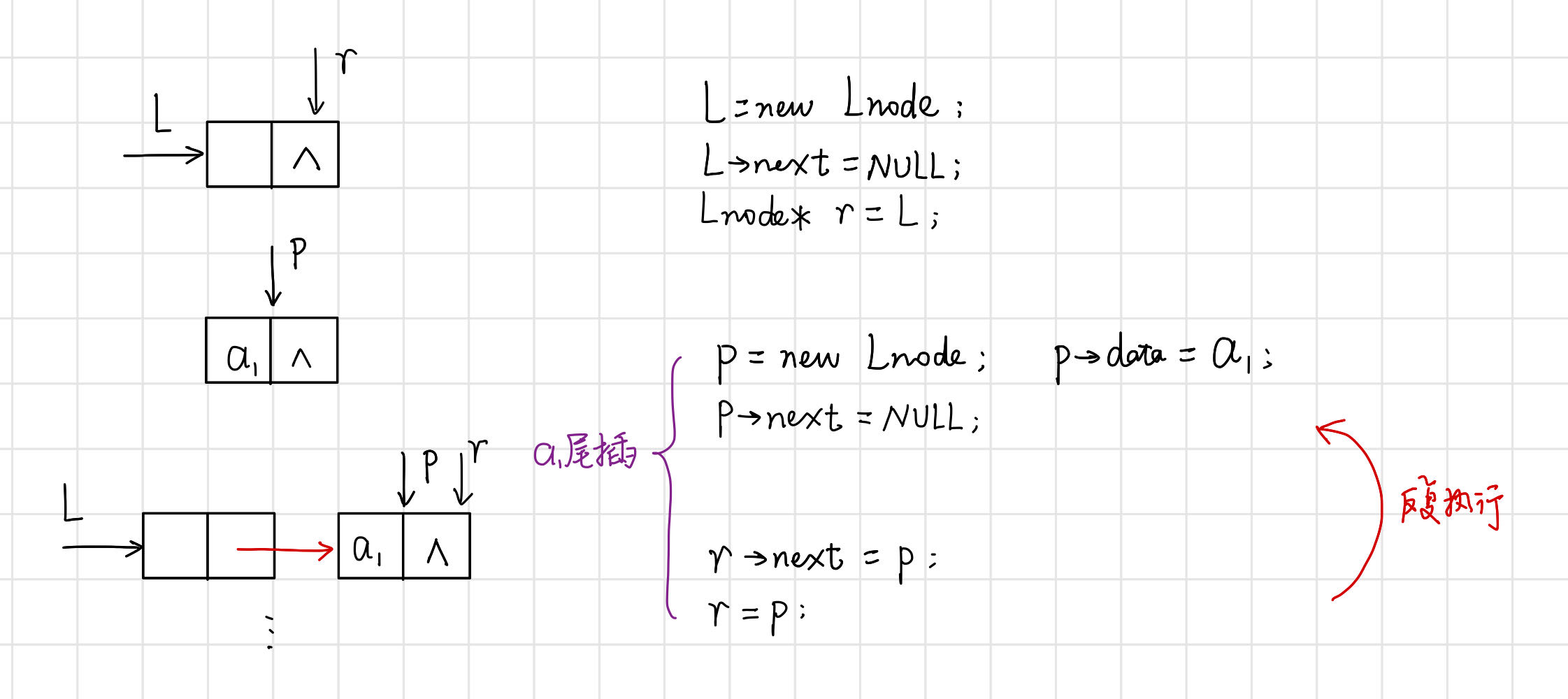
【代码】 。
// 建立单链表:尾插法
void CreateList_R(LinkList& L, int n) {
L = new Lnode;
L->next = nullptr;
Lnode* r = L; // 尾指针r指向头结点
for (int i = 0; i < n; i++) {
Lnode* p = new Lnode; // 输入新结点
std::cin >> p->data; // 输入元素值
p->next = nullptr; // 指针域置空
r->next = p; // 插入到表尾
r = p; // r指向新的尾结点
}
}
【算法分析】 。
建立单链表 时间复杂度为:O(n) 。
双向链表:在单链表的每个结点里再增加一个指向其直接前驱的指针域prior,这样链中就形成了两个方向不同的链,故称为双向链表.

双向循环链表:让头结点的前驱指针指向链表的最后一个结点;让最后一个节点的后继指针指向头结点.
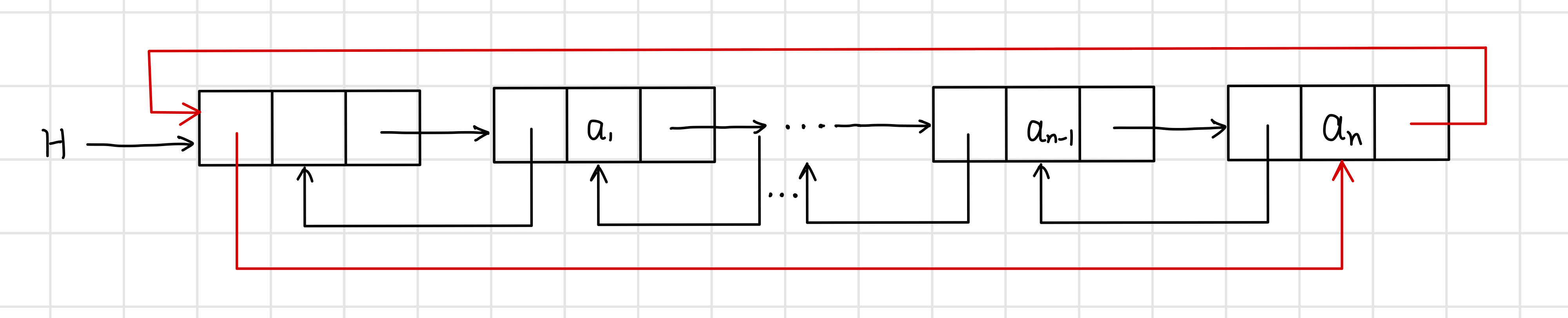
双向链表的结构定义 。
// 双向链表结点结构定义
typedef struct DuLnode {
ElemType data;
struct DuLnode* prior, * next;
}DuLnode, *DuLinkList;
双向链表结构具有 对称性 (设指针p指向某一结点):
p -> prior -> next = p = p ->next -> prior 。
在双向链表中有些操作(求表长、取值等),因仅涉及一个方向的指针,所以他们的算法与线性链表相同。但在插入、删除时,则需要同时修改两个方向上的指针,两者的时间复杂度都为O(n).
【算法思路】 。

【代码】 。
// 双向链表的插入
int ListInsert_Dbl(DblLinkList& L, int i, ElemType e) {
// 先找到第i个元素的位置
DblLnode* p = L->next;
int j = 1;
while (p != L && j < i) {
p = (DblLnode*)p->next;
j++;
}
if (p == L || i < 1) return 0; // i<1或i超过表长+1,插入位置非法
// 插入新结点
DblLnode* s = new DblLnode;
s->data = e;
s->prior = p->prior; // ①
p->prior->next = s; // ②
s->next = p; // ③
p->prior = s; // ④
return 1;
}
【算法思路】 。
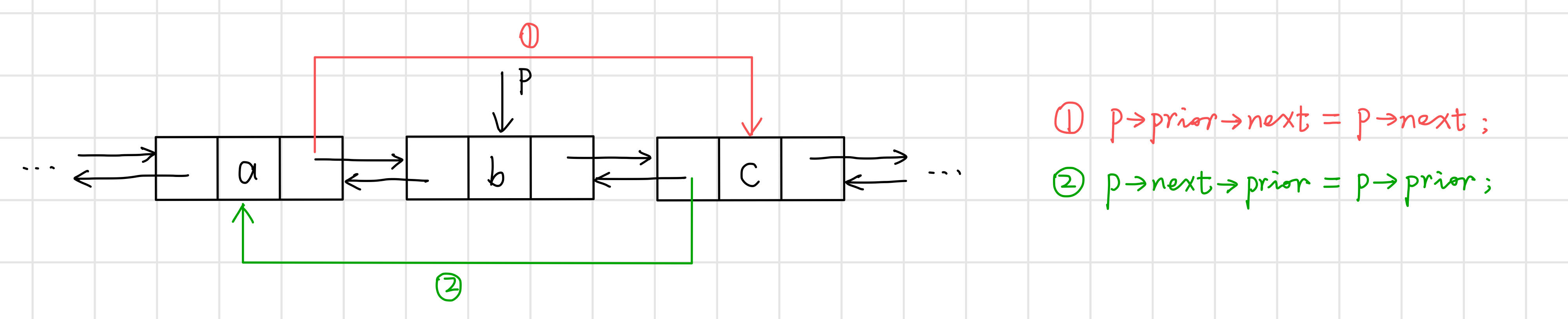
【代码】 。
// 双向链表删除结点
int ListDelete_Dbl(DblLinkList& L, int i, ElemType e) {
// 先找到第i个元素的位置
DblLnode* p = L->next;
int j = 1;
while (p!=L && j < i) {
p = (DblLnode*)p->next;
j++;
}
if (p==L || i < 1) return 0; // i<1或i超过表长,删除位置非法
// 删除新结点
p->prior->next = p->next; // ①
p->next->prior = p->prior; // ②
return 1;
}
循环链表是一种头尾相接的链表,表中最后一个结点的指针域指向头结点,整个链表形成一个环.
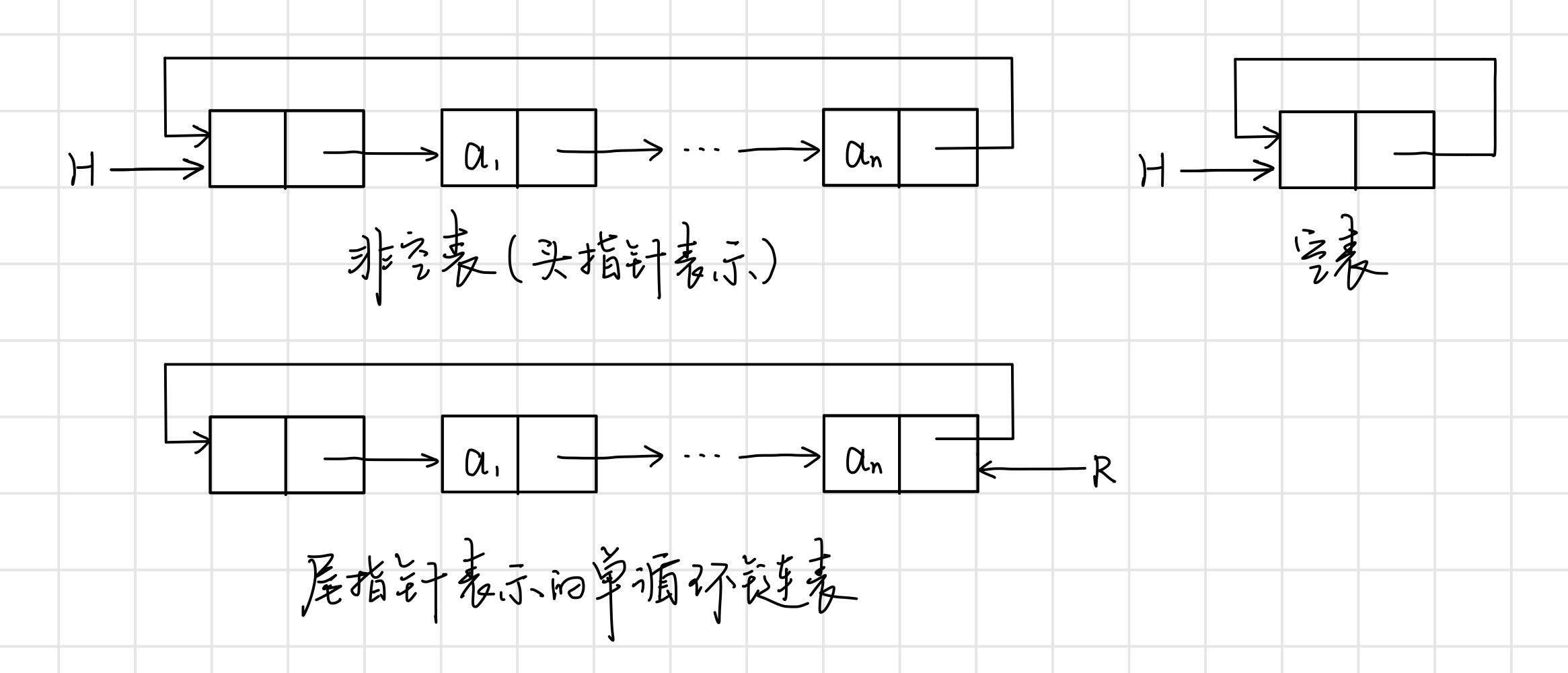
优点: 从表中任一结点出发均可找到表中其他结点.
示例:带尾指针循环链表的合并(将Tb合并在Ta之后) 。
【算法思路】 。
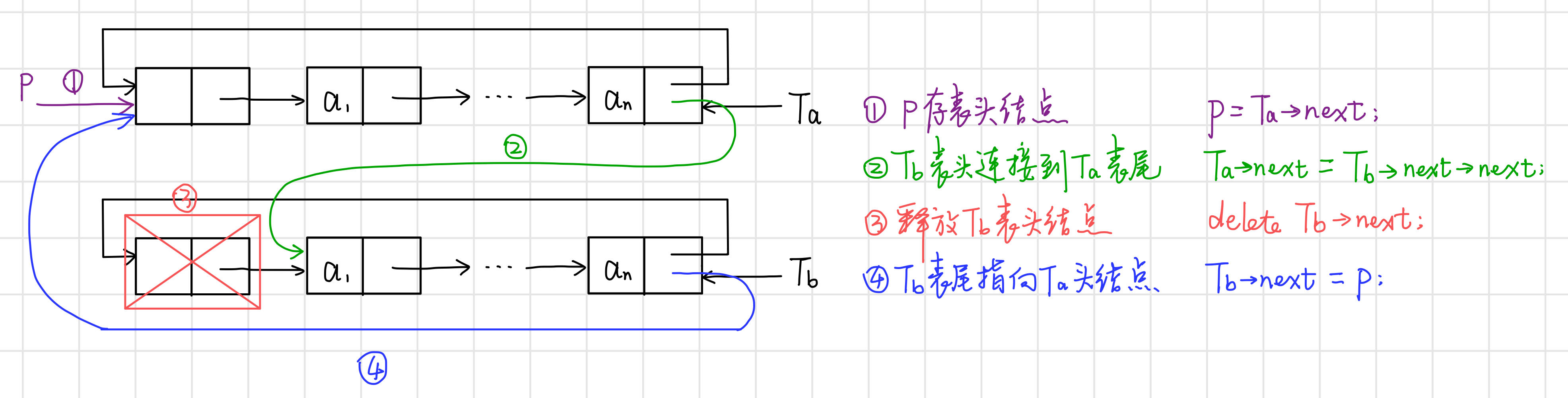
【代码】 。
// 带尾指针循环链表的合并
LinkList Connect(LinkList Ta, LinkList Tb) {
Lnode* p;
p = (Lnode*)Ta->next; // p存表头结点
Ta->next = Tb->next->next; // Tb表头连接到Ta表尾
delete Tb->next; // 释放Tb表头结点
Tb->next = p; // Tb表尾指向Ta头结点
return Tb;
}
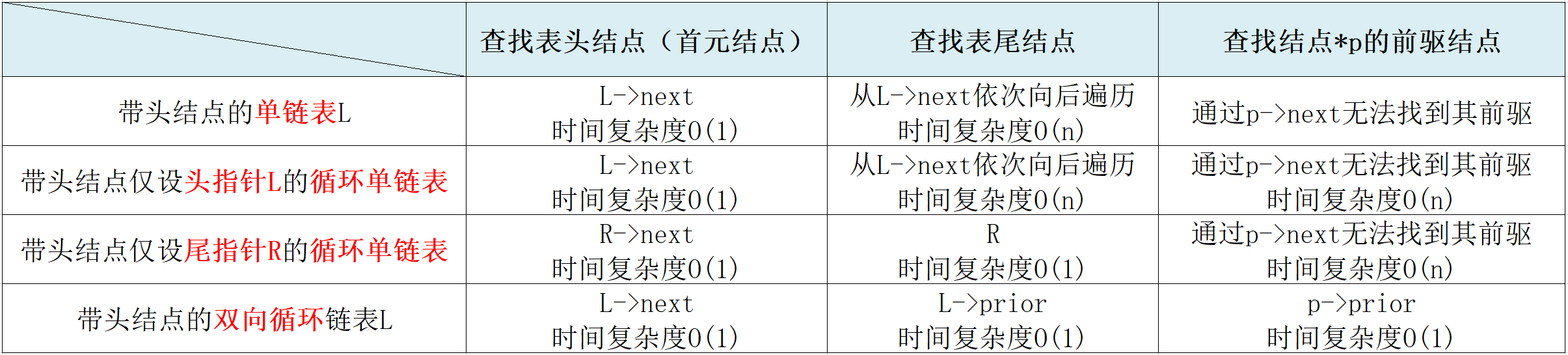
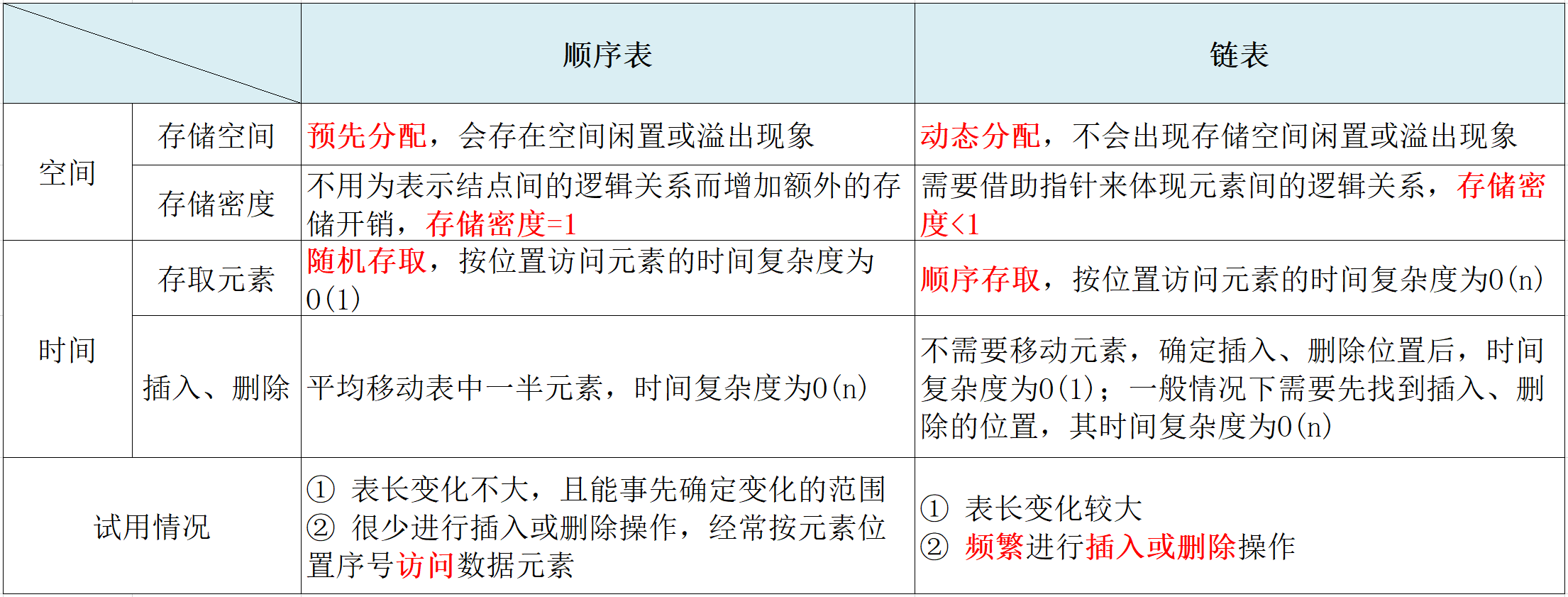
存储密度 定义:
存储密度 = 结点数据本身占用的空间 / 结点占用的空间总量 。
比如单链表某个节点p,其数据域占8个字节,指针域占4个字节,其存储密度 = 8/12 = 67%.
已知线性表La和Lb中的数据元素按值非递减有序排列,现要求将La和Lb归并为一个新的线性表Lc,且Lc中的数据元素仍按值非递减有序排列.
例如:La=(1,7,8) Lb=(2,4,6,8,10,11) → Lc=(1,2,4,6,7,8,8,10,11) 。
(1) 顺序表 实现有序表合并 。
【算法思路】 。
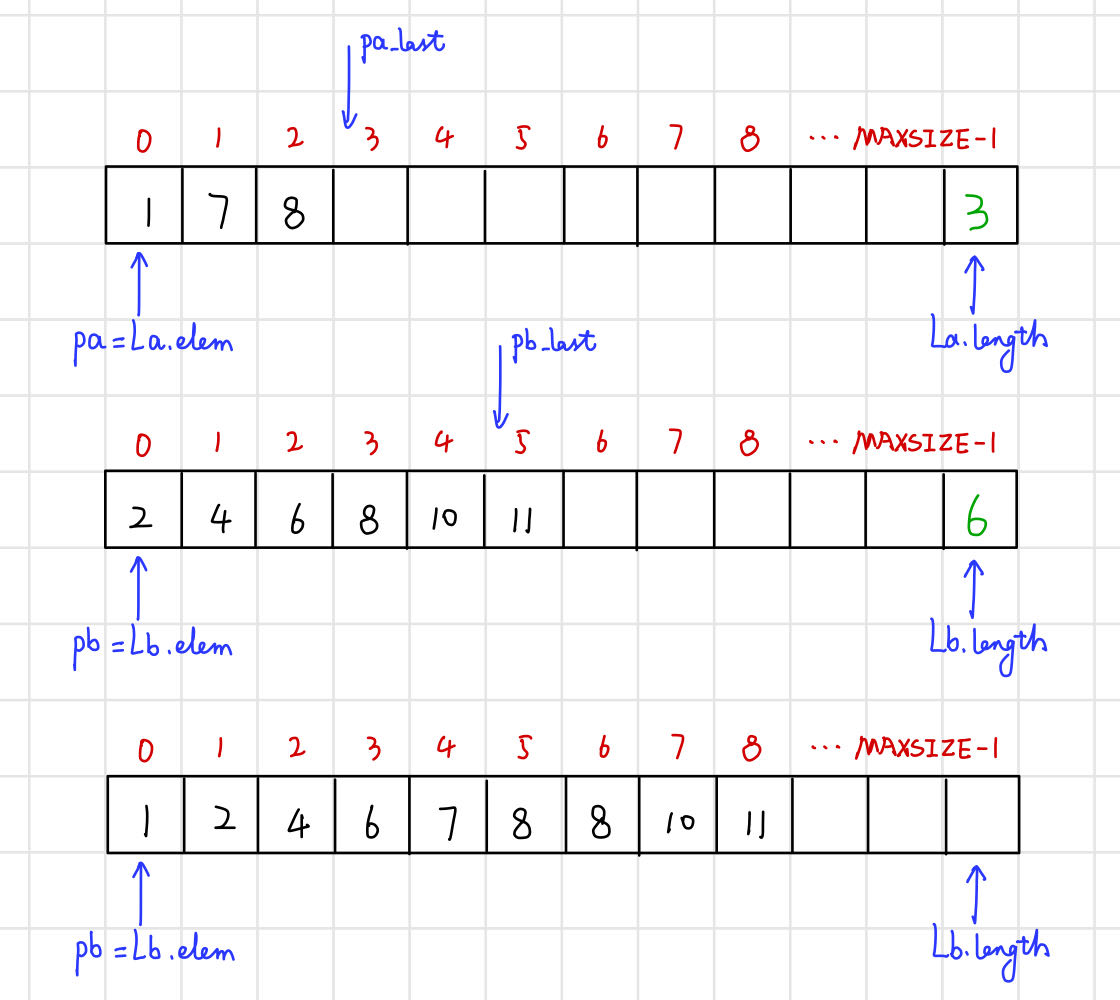
【代码】 。
// 有序表合并:用顺序表实现
void MergeList_Sq(SqList La, SqList Lb, SqList& Lc) {
ElemType* pa = La.elem;
ElemType* pb = Lb.elem; // 指针pa和pb的初值分别指向两个表的第一个元素
Lc.length = La.length + Lb.length; // 新表长为待合并两表的长度之和
Lc.elem = new ElemType[Lc.length]; // 为合并后的新表分配一个数组空间
ElemType* pc = Lc.elem; // 指针pc指向新表的第一个元素
ElemType* pa_last = La.elem + La.length - 1; // 指针pa_last指向La表的最后一个元素
ElemType* pb_last = Lb.elem + Lb.length - 1; // 指针pb_last指向Lb表的最后一个元素
while (pa <= pa_last && pb <= pb_last) {
if (*pa < *pb) *pc++ = *pa++; // 依次“摘取”两表中较小的结点加入Lc
else *pc++ = *pb++;
}
while (pa <= pa_last) *pc++ = *pa++; // Lb表已到达表尾,将La中剩余元素加入Lc
while (pb <= pb_last) *pc++ = *pb++; // La表已到达表尾,将Lb中剩余元素加入Lc
}
【算法分析】 。
时间复杂度: O(ListLength(La) + ListLength(Lb)) 。
空间复杂度: O(ListLength(La) + ListLength(Lb)) 。
(2) 链表 实现有序表合并 。
【算法思路】 。
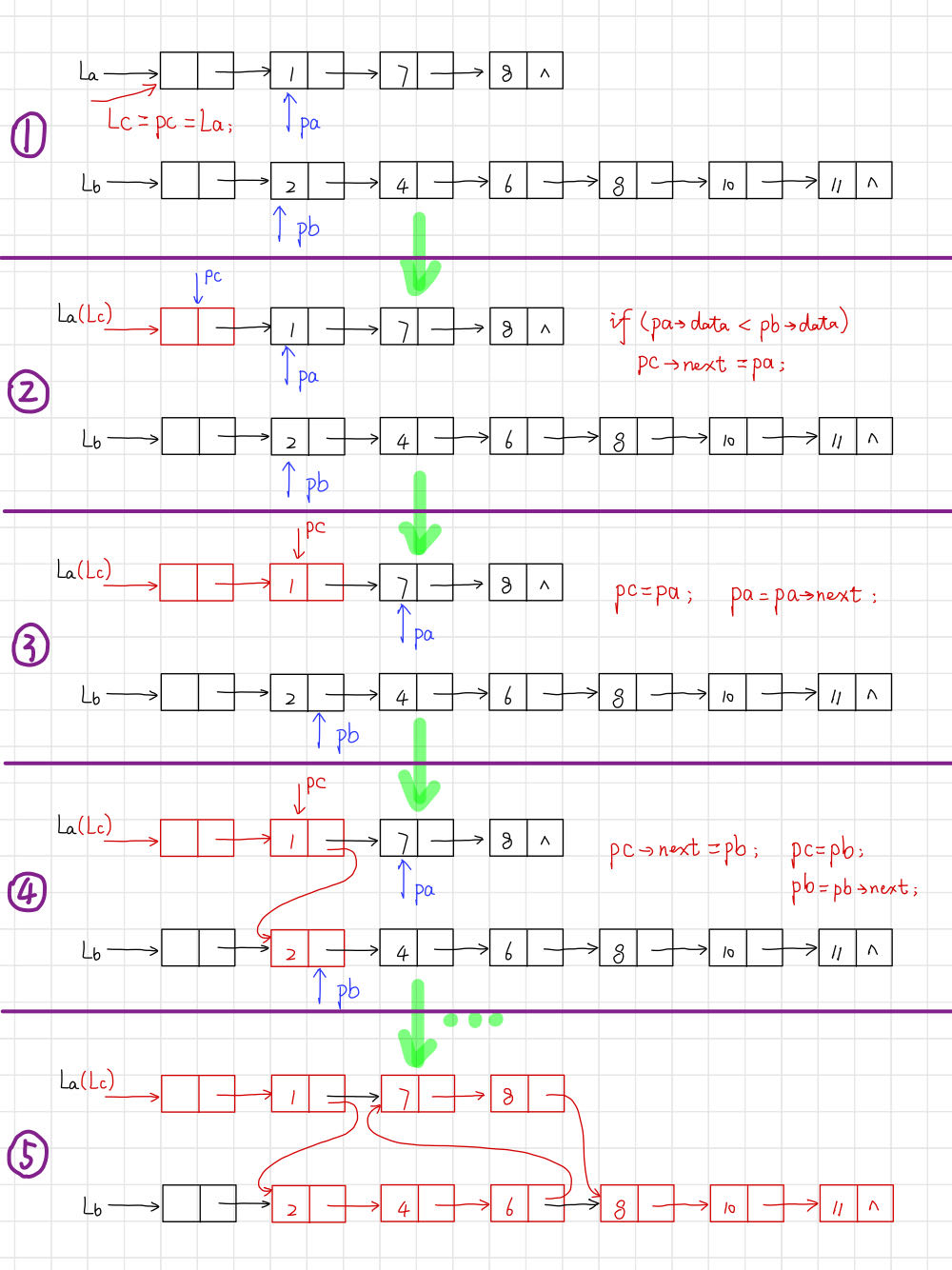
【代码】 。
// 有序表合并:用链表实现
void MergeList_L(LinkList& La, LinkList& Lb, LinkList& Lc) {
Lnode* pa = (Lnode*)La->next;
Lnode* pb = (Lnode*)Lb->next;
Lnode* pc = Lc = La; // 用La的头结点作为Lc的头结点
while (pa && pb) {
if (pa->data <= pb->data) {
pc->next = pa;
pc = pa;
pa = (Lnode*)pa->next;
}
else {
pc->next = pb;
pc = pb;
pb = (Lnode*)pb->next;
}
}
pc->next = pa ? pa : pb; // 插入剩余段
delete Lb; // 释放Lb的头结点
}
【算法分析】 。
时间复杂度: O(ListLength(La) + ListLength(Lb)) 。
空间复杂度: O(1) 。
1. 数据结构与算法基础(青岛大学王卓) 。
2. 数据结构和算法C++实现 。
最后此篇关于【数据结构与算法学习】线性表(顺序表、单链表、双向链表、循环链表)的文章就讲到这里了,如果你想了解更多关于【数据结构与算法学习】线性表(顺序表、单链表、双向链表、循环链表)的内容请搜索CFSDN的文章或继续浏览相关文章,希望大家以后支持我的博客! 。
单向链表 单向链表比顺序结构的线性表最大的好处就是不用保证存放的位置,它只需要用指针去指向下一个元素就能搞定。 单链表图解 图画的比较粗糙,简单的讲解一下: 上面四个长方形,每个长方
使用TCP,我正在设计一些类似于next的程序。 客户端在许多线程中的接收正在等待一台服务器的发送消息。但是,这是有条件的。 recv正在等待特定的发送消息。 例如 客户 thread 1: recv
我正在编写正则表达式来验证电子邮件。唯一让我困惑的是: 顶级域名可以使用单个字符吗?(例如:lockevn.c) 背景:我知道顶级域名可以是 2 个字符到任意字符(.uk、.us 到 .canon、.
是否可以在单个定义中定义同一 Controller 的多个路由? 例如: 我想要一个单一的定义 /, /about, /privacy-policy 使用类似的东西 _home: pat
我正在使用 objective-c开发针对 11.4 iOS 的单 View 应用程序,以及 Xcode版本是 9.4.1。 创建后有Main.storyboard和LaunchScreen.stor
我一直在尝试在 shell 程序中实现管道结构,如果我执行简单的命令(例如“hello | rev”),它就可以工作 但是当我尝试执行“head -c 1000000/dev/urandom | wc
此表包含主机和接口(interface)列UNIQUE 组合* 编辑:这个表也有一个自动递增的唯一 ID,抱歉我应该在之前提到这个 ** | host.... | interface..... |
我想将具有固定补丁大小的“std filter”应用于单 channel 图像。 也就是说,我希望 out[i,j] 等于 img[i,j] 附近的像素值的标准值。 对于那些熟悉 Matlab 的人,
假设我想进行网络调用并使用 rx.Single,因为我希望只有一个值。 我如何应用replay().autoConnect() 这样的东西,这样当我从多个来源订阅时网络调用就不会发生多次?我应该使用
我将图像从 rgb 转换为 YUV。现在我想单独找到亮度 channel 的平均值。你能告诉我如何实现这一目标吗?此外,有没有办法确定图像由多少个 channel 组成? 最佳答案 你可以这样做: #
在比较Go和Scala的语句结束检测时,我发现Scala的规则更丰富,即: A line ending is treated as a semicolon unless one of the foll
在IEEE 1800-2005或更高版本中,&和&&二进制运算符有什么区别?它们相等吗? 我注意到,当a和b的类型为bit时,这些coverpoint定义的行为相同: cp: coverpoint a
我正在使用Flutter的provider软件包。我要实现的是为一个 View 或页面提供一个简单的提供程序。因此,我在小部件中尝试了以下操作: Widget build(BuildContext c
我正在尝试在 cython 中使用 openmp。我需要在 cython 中做两件事: i) 在我的 cython 代码中使用 #pragma omp single{} 作用域。 ii) 使用#pra
我正在尝试从转义字符字符串中删除单引号和双引号。它对单引号 ' 或双自动 " 不起作用。 请问有人可以帮忙吗? var mysting = escapedStr.replace(/^%22/g, '
我正在尝试在 cython 中使用 openmp。我需要在 cython 中做两件事: i) 在我的 cython 代码中使用 #pragma omp single{} 作用域。 ii) 使用#pra
我正在使用 ANT+ 协议(protocol),将智能手机与 ANT+ USB 加密狗连接,该加密狗通过 SimulANT+ 连接到 PC。 SimulANT+ 正在模拟一个心率传感器,它将数据发送到
有人可以解释/理解单/多线程模式下计算结果的不同吗? 这是一个大约的例子。圆周率的计算: #include #include #include const int itera(100000000
我编写了一个粗略的阴影映射实现,它使用 6 个不同的 View 矩阵渲染场景 6 次以创建立方体贴图。 作为优化,我正在尝试使用几何着色器升级到单 channel 方法,但很难从我的着色器获得任何输出
尝试使用 Single-Spa 构建一些东西并面临添加到应用程序 AngularJS 的问题。 Angular2 和 ReactJs 工作完美,但如果添加 AngularJS 并尝试为此应用程序使用

我是一名优秀的程序员,十分优秀!