- Java锁的逻辑(结合对象头和ObjectMonitor)
- 还在用饼状图?来瞧瞧这些炫酷的百分比可视化新图形(附代码实现)⛵
- 自动注册实体类到EntityFrameworkCore上下文,并适配ABP及ABPVNext
- 基于Sklearn机器学习代码实战
python是一门面向对象的编程语言。何为对象?对象是类的实例。在生活中,任何一个事物都是一个对象,如牡丹花。牡丹花的类是花类,同样属于花类的还有荷花、月季花、金银花、菊花、梅花、兰花等,它们都是花科,但是每一朵花都有不同的枝叶,不同的色彩,不同的长相。这就是花类的各个属性了,如玫瑰花是红色,菊花是黄色……除了属性,对象里还有方法,也就是花儿怎样开花,怎样长出形态等.
我们来剖析一下分数的构成,一个分数由 分子、分母构成,分子在上,分母在下。分子可以取任意整数,分母的值不能等于0.
现在我们就可以创建一个分数类:
class
Fraction:
def __init__
(self, top, bottom): self.num = top self.den = bottom
。
所有的类都应该写构造方法,在python中,构造方法一般是__init__。Self是一个总是指向对象本身的特殊参数,它必须是第一个形式参数。然而,在调用方法时,从来不需要提供相应的实际参数.
在构造函数中,self.num与self.den定义了分子与分母,也就是说,调用对象时传入的初始值给其二者赋予:
Myfra = Fraction(3, 5)
。
#创建了一个对象Myfra,并给予初始值3和5,对应分子分母,所以为三分之五 。
如果我们要将此对象的值(也就是三分之五)打印出来,我们则需要定义一个show()方法:
def
show(self):
print(str(self.num)+“/”+ str(self.den))
。
然后我们调用这个方法:
Myfra.show()
。
这样就可以显示出它的值了。但其实我们有更好的实现:
def __str__
(self):
return str(self.num) +“/ ”+str( self.den))
。
因为python中有一套标准方法,我们可以重写它们,也就是重新定义他们,来使我们的程序更加简便。如此调用过程则为:
Myfra = Fraction(3, 5
)
print(Myfra)
。
我们可以根据这种方式来重新其他的标准方法,如实现分数之间的加法运算:
def __add__
(self, otherFraction):
newNum = self.num * otherFraction.den +
\ self.den * otherFraction.num newDen = self.den * otherFraction.den return Fraction(newNum, newDen)
。
如果要使得两个分数相加,最简单的方法就是:
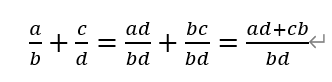
。
由上式可得上述程序,接着调用:
F1 = Fraction(1,4
)
F2 = Fraction(1,2
) F3 = F1 + F2 print(F3)
。
上述程序虽然可以相加,但不是最简分数,我们可以运用欧几里得算法寻得最大公因数(GCD),然后将分子分母分别除以最大公因数,结果就是最简分数.
欧几里得算法中,对于整数m和n,如果m能被n整除,那么它们的最大公因数就是n。如果m不能被n整除,那么结果是n与m除以n的余数的最大公因数.
def
gcd(m, n):
while m % n !=
0: oldm = m oldn = n m = oldn n = oldm% oldn return n
。
我们通过上述程序可以迭代出最大公因数,但是需要注意的是,此程序的分数不能为负数.
#改良版分数的加法 。
def __add__
(self, otherFraction):
newNum = self.num * otherFraction.den +
\ self.den * otherFraction.num newDen = self.den * otherFraction.den common = gcd(newNum, newDen) return Fraction(newNum // common, newDen // common)
。
为了让两个分数进行比较,还需要怎加一个方法,我们可以通过重写内置方法__eq__来实现.
def __eq__
(self, other):
firstNum = self.num *
other.den secNum = other.num * self.den return firstNum == secNum
。
如果我们没有重写__eq__方法,那么默认比较的是两个对象实例,如果是指向同一个实例的对象,那么他们两个才能相等,这被称为 浅相等 。而我们重写后,两个对象只有值相同时,才是相等的,这被称为 深相等 .
所有代码如下:
class
Fraction:
def __init__
(self, top, botton): self.num = top self.den = botton def __str__ (self): return str(self.num) + "/" + str(self.den) def __add__ (self, otherFraction): newnum = self.num * otherFraction.den + self.den * otherFraction.num newden = self.den * otherFraction.den common = gcd(newnum, newden) return Fraction(newnum // common, newden // common) def __eq__ (self, otherFraction): firstnum = self.num * otherFraction.den secnum = self.den * otherFraction.num return firstnum == secnum def gcd(m, n): while m % n != 0: oldm = m oldn = n m = oldn n = oldm % oldn return n if __name__ == '__main__' : f1 = Fraction(3, 4 ) f2 = Fraction(3, 4 ) f3 = f1 + f2 print (f3) print(f1 == f2) f4 = Fraction(4, 8 ) f5 = Fraction(2, 4 ) print(f4 == f5) print(f4 + f5)
。
最后此篇关于Python面向对象(上)的文章就讲到这里了,如果你想了解更多关于Python面向对象(上)的内容请搜索CFSDN的文章或继续浏览相关文章,希望大家以后支持我的博客! 。
我正在创建一个多区域 AlwaysOn Sql Availability 组。我在东部有 2 个虚拟机,在西部有 1 个虚拟机。我需要使用面向公众的负载平衡器对这些进行负载平衡。是否可以使用存在于不同
就目前而言,这个问题不适合我们的问答形式。我们希望答案得到事实、引用或专业知识的支持,但这个问题可能会引起辩论、争论、投票或扩展讨论。如果您觉得这个问题可以改进并可能重新打开,visit the he
我是 Smalltalk 技术的新手。我的编程经验是使用 C 和 C++。我想了解smalltalk的设计方法论。谁能推荐一些用smalltalk开发的简单的实时应用程序,可以帮助像我这样的初学者探索
现在我已经对 web2py 比较熟悉了,我想试试 Django。 主要区别是什么? 考虑到 web2py 知识,最有效的入门方法是什么? (一定有一些python应用框架的知识,不是吗?) 编辑 另外
我之前发过一个问题,Moving away from VSS ,其中我向使用 VSS 的 Delphi 开发人员询问了最佳的 VCS 控件。大多数开发人员似乎将 svn 与 TortoiseSVN 一
引用this question ,收集对 Delphi 初学者真正有帮助的网站链接可能会很好。 第一个答案指向Delphi Basics ,这是一个非常好的网站。 但一定还有更多。 所以:请为这个社区
我已经构建了一个 saas 产品,其中 Angular 4 与 golang Rest api 集成,并将构建上传到了 aws ec2 实例上。我的项目是一个基于 Multi-Tenancy 的应用程
我是 .NET 开发人员,在此之前使用过 VB6。我已经非常熟悉这些环境,并在垃圾收集语言的上下文中工作。但是,我现在希望通过 native C++ 增强我的技能,但发现自己有点不知所措。具有讽刺意味
就目前情况而言,这个问题不太适合我们的问答形式。我们希望答案得到事实、引用资料或专业知识的支持,但这个问题可能会引发辩论、争论、民意调查或扩展讨论。如果您觉得这个问题可以改进并可能重新开放,visit
由于我在数学方面没有任何出色的技能,所以我问您是否存在我应该在未来可能会改变的类(class)中使用的算法。 考虑以下场景: “角色”类具有以下字段: private boolean admin; p
我有许多面向“列”的 csv 文件,我需要对其进行预处理才能最终索引它们。 这是面向时间的数据,每个“设备”都有大量的列(最多 128 列),例如: LDEV_XXXXXX.csv
我想就重构技巧的最佳资源展开讨论,着眼于前端 JavaScript 重构。 一个我尊重其意见的 friend 建议这个 book ,尽管它使用 Java 中的示例。我明白 OO 重构的原则应该翻译成另
我不明白如何使用 Jquery/javascript 处理对象。 以及如何创建私有(private)方法/变量?我在论坛上看到关闭,但我尝试过但没有用。以及如何查看方法/变量是否是私有(private
我已经使用 MATLAB 多年并且非常熟练。我习惯了 MATLAB 调试,您可以在其中跳过行并查看变量及其变化方式,这就是我学习编码的方式。我现在正在研究使用 FORTRAN、C++ 和 Python
我正在学习如何实现“单一 Activity - 多个 fragment ”架构。据我所知,这是如今很普遍的方法,你可以找到很多关于这个主题的文章。例如这个 http://vinsol.com/blog
目前是否有任何简单的方法可以在 Apache Tomcat Servlet 容器前面设置 YAWS Web 服务器,类似于流行的 Apache httpd + Tomcat 设置? 最佳答案 我不相信
我是一个相当有能力的 Ruby 脚本编写者/程序员,但一直感到要扩展到 C++ 的压力。我没能找到任何与“C++ for Ruby Programmers”相关的网站。 This site Pytho
关闭。这个问题不符合Stack Overflow guidelines .它目前不接受答案。 我们不允许提问寻求书籍、工具、软件库等的推荐。您可以编辑问题,以便用事实和引用来回答。 关闭 5 年前。
按照目前的情况,这个问题不适合我们的问答形式。我们希望答案得到事实、引用或专业知识的支持,但这个问题可能会引发辩论、争论、投票或扩展讨论。如果您觉得这个问题可以改进并可能重新打开,visit the
我在表上有一个名为 cart_product_fti 的全文索引 每当我使用它时,我都必须准确列出索引中的所有字段: MATCH (foo,bar,etc) 我的想法是,如果稍后我决定向索引添加/删除

我是一名优秀的程序员,十分优秀!